字体
罗马字体 \mathrm{}
for i in range(97, 123):
print('$\\mathrm{{{0}}}$'.format(chr(i)))
$\mathrm{*}$
for i in range(65, 91):
print('$\\mathrm{{{0}}}$'.format(chr(i)))
$\mathrm{*}$
在这里插入图片描述
斜体 \mathit{}
$\mathit{*}$
for i in range(97, 123):
print('$\\mathit{{{0}}}$'.format(chr(i)))
在这里插入图片描述
for i in range(65, 91):
print('$\\mathit{{{0}}}$'.format(chr(i)))
在这里插入图片描述
粗体 \mathbf{}
$\mathbf{*}$
for i in range(97, 123):
print('$\\mathbf{{{0}}}$'.format(chr(i)))
在这里插入图片描述
for i in range(65, 91):
print('$\\mathbf{{{0}}}$'.format(chr(i)))
在这里插入图片描述
无衬线-f \mathsf{}
$\mathsf{*}$
for i in range(97, 123):
print('$\\mathsf{{{0}}}$'.format(chr(i)))
for i in range(65, 91):
print('$\\mathsf{{{0}}}$'.format(chr(i)))
打字机字体 \mathtt{}
$\mathtt{*}$
for i in range(97, 123):
print('$\\mathtt{{{0}}}$'.format(chr(i)))
for i in range(65, 91):
print('$\\mathtt{{{0}}}$'.format(chr(i)))
书法字体 \mathcal{}
$\mathcal{*}$
for i in range(65, 91):
print('$\\mathcal{{{0}}}$'.format(chr(i)))
在这里插入图片描述
注:小写字母貌似没有
黑板粗体 \mathbb{} \usepackage{amssymb}
$\mathbb{*}$
for i in range(65, 91):
print('$\\mathbb{{{0}}}$'.format(chr(i)))
在这里插入图片描述
注: 小写字母貌似没有
德文尖角体 \mathfrak{} \usepackage{amssymb}
$\mathfrak{*}$
for i in range(97, 123):
print('$\\mathfrak{{{0}}}$'.format(chr(i)))
for i in range(65, 91):
print('$\\mathfrak{{{0}}}$'.format(chr(i)))
花体 \mathscr{} \usepackage{mathrsfs}
$\mathscr{}$
for i in range(65, 91):
print('$\\mathscr{{{0}}}$'.format(chr(i)))
注:小写貌似没有
数学符号表(摘自《140分钟学会LaTex》)
数学模式重音符号(头顶上的那玩意)
希腊字母
二元关系
$\not\in$
二元运算符
“大”运算符
箭头
定界符
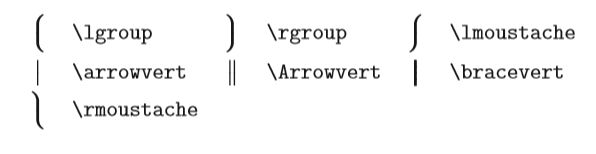
大定界符
其他符号(AMS的符号就不贴了)
一些数学公式写法的例子
$\mathbf{Var}[(CR)_{ij}] = \mathop{\sum}\limits_{t=1}^{c}\mathbf{Var}[X_t]
=\mathop{\sum}\limits_{k=1}^{n}\frac{A_{ik}^{2}B_{kj}^{2}}{cp_k}
-\frac{1}{c}(AB)_{ij}^2$
\begin{displaymath}
\begin{array}{ll}
\min & E[\|AB-CR\|_F^2]\\
s.t. & \mathop{\sum}\limits_{i=1}^{n}p_i = 1
\end{array}
\end{displaymath}
#\usepackage{amssymb, amsmath}
\[
\begin{split}
x_k = & x_{k-1} + \gamma_k[A_kx_{k-1}-(x_{k-1}^{\top}A_kx_{k-1})x_{k-1}]\\
=& x_{k-1} + \gamma_k[Ax_{k-1}-(x_{k-1}^{\mathrm{T}}Ax_{k-1})x_{k-1}]\\
&+\gamma_k[(A_k-A)x_{k-1}-(x_{k-1}^{\top}(A_k-A)x_{k-1})x_{k-1}
\end{split}
\]
\begin{equation} \label{eq:1}
\frac{\mathrm{d}\|z\|_2^{2}}{\mathrm{d}t} = 2z\frac{\mathrm{d}z}{\mathrm{d}t} = 0
\end{equation}
#\ref{eq:1}引用
$\underbrace{a+b+\cdots+z}_{26}$
\begin{displaymath}
\mathbf{X} =
\left( \begin{array}{ccc}
x_{11} & x_{12} & \ldots \\
x_{21} & x_{22} & \ldots \\
\vdots & \vdots & \ddots
\end{array} \right)
\end{displaymath}
\begin{displaymath}
y = \left\{ \begin{array}{ll}
a & \textrm{if $d>c$}\\
b+x & \textrm{in the morning}\\
l & \textrm{all day long}
\end{array} \right.
\end{displaymath}
\begin{displaymath}
\left(\begin{array}{c|c}
1 & 2 \\
\hline
3 & 4
\end{array}\right)
\end{displaymath}
\begin{displaymath}
{}^{12}_{\phantom{1}6}\textrm{C}
\qquad \textrm{versus} \qquad
{}^{12}_{6}\textrm{C}
\end{displaymath}
\begin{displaymath}
\frac{\mathrm{d}f}{\mathrm{d}\theta}=
\mathrm{(\cos \theta, -\sin \theta)}
\left(\begin{array}{cc}
\mathrm{x_1^T}\\
\mathrm{x_2^T}
\end{array} \right)
\mathrm{A}
\mathrm{(x_1, x_2)}
\left(\begin{array}{cc}
\sin \theta\\
\cos \theta
\end{array} \right)
\end{displaymath}