nodejs之inherits
进位计数制
生活中我们常用的是10进制,但在计算机中数据都是以2进制的形式保存的。因此,熟练掌握2进制的特点和运算是编写程序并不可少的前提。
一般来说,进位计数制包含三个要素:
- 数制使用的数码:十进制含10个数码0~9,二进制含2个数码0和1等。
-
进位规则:十进制为逢十进一,二进制为逢二进一等。
-
每一个数位上数码所具有的权:十进制数码各位的权是以10为底的幂,二进制数码各位的权是以2为底的幂。
一般而言,对于用R进制表示的数N(R为任意正整数),可以按权展开为:
N=Kn×Rn+Kn-1×Rn-1+…+K1×R1+K0×R0+K-1×R-1+…+K-m×R-m (公式A)
例:828.8 = 8×102+2×101+8×100+8×10-1,这里必须要注意的是任何进制中个位数的权值都是1,从右往左权值越来越大。
常用进制
在计算机中,常用的进制有四种:2进制(代号B),8进制(代号O),16进制(代号H)和10进制(代号D),其中16进制所用的数码为0-9和A-F(A代表10,F代表15)。这里之所以加入了8进制和16进制,是因为用2进制表达数值需要的位数往往很大,不便于书写和阅读。
不同的进位计数制之间需要进行转换,而且以10进制与2进制之间的转换为主,需要熟练掌握。另外为了今后的计算方便,最好能够熟练掌握0-15之间的各进制的表示,这会大大方便今后的学习。
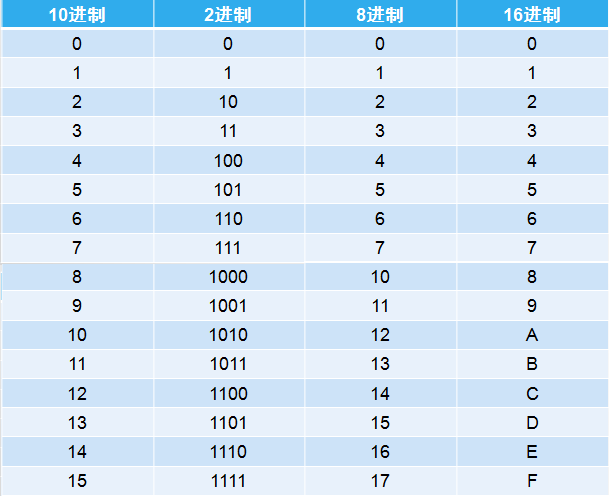
进制转换
1、任意进制转换为10进制:任意R进制数转换成十进制数比较简单,只需按权展开然后相加,其和便是相应的十进制数。这种方法称为按权相加法。
这里还是需要提醒一下,计算权值的时候需要从个位开始数起,往左递增,往右递减。
例:求与(11011.01)2等值的十进数
(11011.01)2=1×24+1×23+0×22+1×21+1×20+0×2-1+1×2-2=16+8+0+1+0+0.25=(27.25)10
(35B)16=3×162+5×161+11×160=768+80+11=(859)10
2、10进制整数转换为其他进制:这里主要用的是除基取余法。
由上面的公式A容易得知:将N除以R之后,K0这一项就成为了本次除法的余数,然后继续重复该过程,就依次取得了K1,K2直至Kn,当数变成0的时候过程结束。
注意这里是倒序的过程,首先取得的数反而是在最后面。
例:将10进制的18转换为2进制,推演过程如下。

所以(18)10=(10010)2
将10进制的数转换为其他进制的方法是雷同的。
例:100除以16余数为4商为6,因此K0=4;6除以16余数为6商为0,因此K1=6,所以(100)10=(64)16。
3、2进制与8进制、16进制间的转换
二进制数转换成八进制数的方法可以概括为“三位并一位”,八进制数转换成二进制数的方法可以概括为“一位拆三位”;
二进制数转换成十六进制数的方法可以概括为“四位并一位”,十六进制数转换成二进制数的方法可以概括为“一位拆四位”
例: 将 (11101.1101)2转换成八进制数。
解: 0 1 1 1 0 1 . 1 1 0 1 0 0
3 5 6 4
所以 (11101.1101)2=(35.64)8
这里特别要注意的是,如果位数不正好是3或4的倍数的话,需要在整数位的最前方和小数位的最后方补0,这样才不会改变原有数的值。
解: 2 5 . C 4
0010 0101 1100 0100
所以 (25.C4)16=(100101.110001)2
另外,任意进制间的小数转换比较复杂且很可能会得到无限循环的小数,这里就不展开了。
总结与提示
1、掌握和了解不同的进制是学习计算机编程的必备环节,特别是2进制的内容和计算,必须熟练掌握。
2、将10进制转换为2进制,用除基取余法显得有些笨重,而且运算次数过多。在下一个专题中,将介绍一种相对简便快捷的方法。
3、8,16进制和2进制的转换,需要注意必须从个位数开始进行数数。如(11111)2=(37)8,而不是(76)8,补0只能补在最前或者最后,不能补在中间。