paviaU光谱数据集降维与分类
基于高光谱数据集PaviaU的数据降维与分类
一、项目问题来源
高光谱图像分类是高光谱遥感对地观测技术的一项重要内容,在军事及民用领域都有着重要的应用。然而,高光谱图像的高维特性、波段间高度相关性、光谱混合等使高光谱图像分类面临巨大挑战。一方面高光谱图像相邻波段之间相关性较大,存在较高的信息冗余。另一方面,对高光谱图像蕴含的丰富的谱信息直接进行处理所需计算量巨大,高光谱图像中存在异物同谱及同谱异物问题,导致数据结构呈高度非线性,极大增加了分类的难度。在早期的高光谱图像分类技术中,仅利用丰富的光谱信息,没有更深入挖掘数据内在信息,例如距离分类器、K近邻分类器、最大似然分类器等,这些方法大多会受到Hughes现象的影响,在训练集有限情况下,分类的精度会随着数据维度的增大而大幅度下降。
图1:Hughes 现象
针对这一个问题,研究者们提出一些特征提取的方法,例如主成分分析、线性判断分析、独立成分分析等,将高维数据映射到一个低维空间,同时保留类别信息。
本篇博客的目的在于,通过对高光谱数据集paviaU进行降维与分类,学习熟悉数据降维方法PCA、KPCA、LDA与分类方法例如KNN、SVM以及CNN等,并用Matlab实现便于比较分析。同时对高光谱图像分类有一个初步的认识。
二、高光谱数据集选择
如上图所示为高光谱图像分类常用数据集,综合考虑已标记的样本量、波段数、空间分辨率、数据大小等因素,在网上可以下载到相应资源的前提下,选取Pavia University 高光谱数据集作为本次project的实验对象。
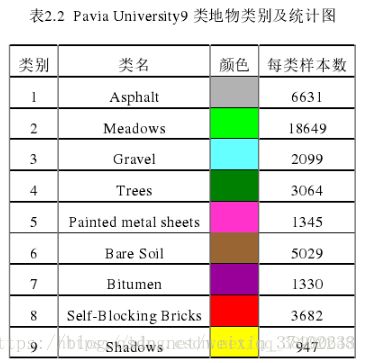
Pavia University 数据是由德国的机载反射光学光谱成像仪(Reflective Optics Spectrographic Imaging System,ROSIS-03)在 2003 年对意大利的帕维亚城所成的像的一部分高光谱数据。该光谱成像仪对 0.43-0.86μm 波长范围内的 115 个波段连续成像,所成图像的空间分辨率为 1.3m。其中 12 个波段由于受噪声影响被剔除,因此一般使用的是剩下 103 个光谱波段所成的图像。该数据的尺寸为 610×340,因此共包含2207400 个像素,但是其中包含大量的背景像素,包含地物的像素总共只有 42776 个,这些像素中共包含 9 类地物,包括树、沥青道路(Asphalt)、砖块(Bricks)、牧场(Meadows)等。
图2:PaviaU数据类地物类别及统计图 图3:可视化图
图4:PaviaU场景光谱响应曲线
我在每类样本选取200个作为训练集,100个作为测试集,共计1800个训练样本与900个测试样本。
三、数据分类算法
3.1 K最近邻分类算法 KNN
3.1.1 KNN简介
KNN(K-Nearest Neighbor)算法即K最邻近算法,是实现分类器中比较简单易懂的一种分类算法。即人们在观察事物,对事物进行分类的时候,人们最容易想到的就是谁离那一类最近谁就属于哪一类,即俗话常说的“近朱者赤,近墨者黑”,人们自然而然地把这种观察方式延伸到数据分类处理领域。K-NN算法就是基于欧几里得距离推断事物类别的一种实现方法。
3.1.2 KNN Matlab实现
KNN可以按如下步骤利用Matlab实现,其函数代码就用六行即可实现。
①计算测试数据与各个训练数据之间的距离;
②按照距离的递增关系进行排序;
③选取距离最小的K个点;
④确定前K个点所在类别的出现频率;
⑤返回前K个点中出现频率最高的类别作为测试数据的预测分类。
3.1.3关于K值的选取
KNN简单易懂,其算法关键在于K值的选取,在本次project中,我通过KNN对Pavia原始数据集进行分类,改变K值的大小并观察KNN分类准确度的变化,发现在K=8时,在测试集上分类准确度最高,为93.56%。
![]()
图5:K值的选取与分类准确度的关系示意图
k值选择过小,得到的近邻数过少,会降低分类精度,同时也会放大噪声数据的干扰;而如果k值选择过大,并且待分类样本属于训练集中包含数据数较少的类,那么在选择k个近邻的时候,实际上并不相似的数据亦被包含进来,造成噪声增加而导致分类效果的降低。如何选取恰当的K值也成为KNN的研究热点。k值通常是采用交叉检验来确定(以k=1为基准)。经验规则是k一般低于训练样本数的平方根。
3.2 SVM支持向量机
3.2.1 SVM简介
在机器学习中,支持向量机(support vector machine,常简称为SVM,又名支持向量网络)是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。SVM的工作原理是将数据映射到高维特征空间,这样即使数据不是线性可分,也可以对该数据点进行分类。
3.2.2 SVM参数设置
由于SVM是二分分类模型,而PaviaU数据集中共有9个类别,所以在libsvm中,采用one- versus-one法进行多分类。其做法是在任意两类样本之间设计一个SVM,因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。Libsvm中的多类分类就是根据这个方法实现的。
在libsvm中,对于分类问题,我们可以选择C-SVC模型与nu-SVC模型。C-SVC中c的范围是1到正无穷。nu-SVC中nu的范围是0到1,代表错分样本所占比例的上界,支持向量所占比列的下界。核函数有线性核函数、多项式核函数、高斯核函数、sigmoid核函数四种可以选择,在简单设置相应的参数后,对比比较利用各种分类模型与核函数对PaviaU数据集进行分类,在测试集上得到的分类结果精确度如下表所示:
| 分类模型 |
核函数 |
测试集准确度 |
| C-SVC模型 |
线性核函数 |
92.5556% |
| 多项式核函数 |
97.4444% |
|
| 高斯核函数 |
89.3333% |
|
| sigmoid核函数 |
74.1111% |
|
| nu-SVC模型 |
线性核函数 |
89.8889% |
| 多项式核函数 |
82.2222% |
|
| 高斯核函数 |
85.7778% |
|
| sigmoid核函数 |
85.8889% |
SVM引入核函数有两个方面的原因,一是为了更好的拟合数据,另一个重要的原因是实现数据的线性可分。吴恩达老师在coursera中提到,如果特征数量与样本数量差不多,可以选择LR/线性核;如果特征数量小,样本数量正常,则选择高斯核;如果特征数量小,样本数量大,则可以手动添加一些特征。考虑到上述实验结果,并且PaviaU数据集中特征维数为103,每个样本的训练集数量为200,所以在接下来实验中选择C-SVC模型+多项式核函数的方法,其可以轻松达到97.4444%的分类精度。
3.3 卷积神经网络CNN
3.3.1CNN简介
卷积神经网络是近年发展起来,并引起广泛重视的一种高效识别方法。一般地,CNN的基本结构包括两层,其一为特征提取层,每个神经元的输入与前一层的局部接受域相连,并提取该局部的特征。一旦该局部特征被提取后,它与其它特征间的位置关系也随之确定下来;其二是特征映射层,网络的每个计算层由多个特征映射组成,每个特征映射是一个平面,平面上所有神经元的权值相等。
与图像处理中使用的二维卷积不同,在本次PaviaU数据集中所使用的是在光谱维度上的一维卷积,因为PaviaU数据集是以每个像素点作为一个样本。所搭建的卷积神经网络主要由卷积层与池化层构成。
3.3.2CNN网络调参过程
由于卷积层与池化层的设置以及各种初始化参数都会对最后的精度产生影响,因此,在这里记录调参的过程,使训练后的CNN卷积神经网络在测试集的精确度尽可能达到最大。主要考虑的参数如下:学习率、训练集大小、迭代次数、样本批量、卷积神经网络深度、每一个卷积层神经元个数。初始化参数如下,此时在测试集上获得的准确度是94.556%
|
初始化网络结构 (i-6c-3s-12c-6s-o)
Batchsize=5 Learningrate=1 Iteration=200 Trainingsize=200 |
输入层i |
Inputmaps=1 |
|
卷积层c |
Outputmaps=6 |
|
| Kernelsize=5 |
||
| 池化层s |
Scale=3 |
|
|
卷积层c |
Outputmaps=12 |
|
| Kernelsize=6 |
||
| 池化层s |
Scale=4 |
|
| 输出层o |
Outputmaps=9 |
首先从四个初始化参数进行更改,观察在测试集上的准确度。
| 参数 |
初始值 |
更新值 |
参数更新后准确率 |
初始准确率 |
| Batchsize |
5 |
8 |
94.444% |
94.556% |
| Learningrate |
1 |
1.2 |
94.667% |
|
| Iteration |
200 |
500 |
94.778% |
|
| Trainingsize |
200 |
500 |
90.044% |
如上表所示,调整学习率、训练集大小、迭代次数、样本批量的初始化值对最后准确率的影响并不大,在调整训练集的大小后,甚至出现测试集准确率急剧变小的迹象,这可能与CNN模型过拟合有关,有待于进一步的研究。而微调学习率与迭代次数可以一定程度上提升准确度,但是效果不太明显。
于是我们可以改变网络结构,首先改变网络结构,增加卷积层神经元的个数。
| 网络结构 |
准确率 |
| i-6c-3s-12c-6s-o |
94.556% |
| i-6c-3s-15c-6s-o |
95.333% |
如图所示,在增加第二层网络的神经元个数后,准确度有了明显的提升。
然后可以尝试,增大网络的深度。
| 网络结构 |
准确率 |
| i-6c-3s-12c-6s-o |
94.556% |
| i-6c-3s-8c-3s-12c-3s-o |
92.667% |
| i-6c-2s-8c-2s-12c-2s-o |
93.667% |
| i-6c-2s-9c-2s-15c-2s-o |
94.556% |
| i-8c-2s-12c-2s-16c-2s-o |
95.000% |
如上表所示,首先增加了一层卷积层与池化层,准确度有一定程度下降。然后调整了池化层Scale大小,另外再增加每层网络神经元个数,准确度得到一定 程度的提升。综上实验,减小池化层Scale大小并且增加卷积层神经元个数提升测试集准确度效果较好。所以采用i-6c-3s-15c-6s-o的网络结构,其网络层数少,训练时间较短,并且准确度最高。
四、数据降维方法
4.1 主成分分析PCA
4.1.1 PCA原理简介
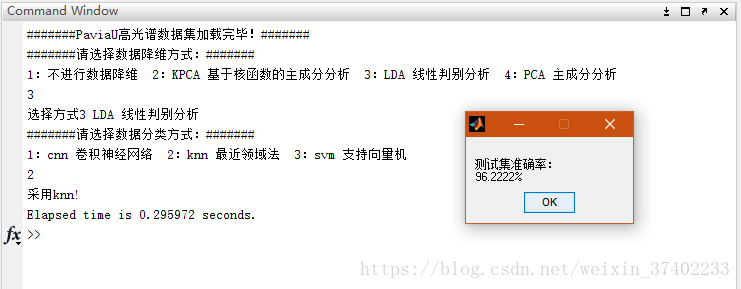
PCA的思想是将n维特征映射到k维空间上k 4.1.2PCA matlab实现步骤 ①对输入数据initialize_mat每一个特征维度求均值,然后在每个特征维度减去均值得meanmat ②对meanmat'*meanmat求特征向量与特征值 ③找出最大的特征值与特征向量,计算投影矩阵project_mat=meanmat*max_v/sqrt(sigma) (为了使投影矩阵归一化) ④计算降维后的矩阵 p_d_mat=project_mat'*meanmat ⑤p_d_mat L2归一化 4.1.3关于降维后特征数个数的选取 PCA降维后特征数目保留多少是我们所关心的问题。我利用高光谱数据集PaviaU做了一个测试,利用PCA将103个光谱特征降维至1~102,然后观察在测试集上svm分类的准确度。可以发现,当pca降维至15个特征左右时,训练集与测试集已经达到较高的准确度。之后几乎维持不变。所以我们选取pca降维之后的特征数量为15。 图6:pca降维后的特征数与svm分类准确度的关系 4.1.4关于投影矩阵归一化与p_d_mat L2归一化 在本次matlab编程实现过程中加入了投影矩阵归一化为单位向量并且对最后输出矩阵进行了L2归一化。我们可以比较归一化与未归一化两种情况。进行归一化后,准确度与降维后特征数目关系曲线变化抖动较小,变化趋势更加稳定。 图7:归一化结果 图8:未归一化的结果 4.2 基于核函数的主成分分析 KPCA 4.2.1 KPCA简介 PCA是利用特征的协方差矩阵判断变量间的方差一致性,寻找出变量之间的最佳的线性组合,来代替特征,从而达到降维的目的,但从其定义和计算方式中就可以看出,这是一种线性降维的方法,如果特征之间的关系是非线性的,用线性关系去刻画他们就会显得低效,KPCA正是应此而生,KPCA利用核化的思想,将样本的空间映射到更高维度的空间,再利用这个更高的维度空间进行线性降维。 KPCA可以挖掘到数据集中蕴含的非线性信息。 4.2.2 KPCA的matlab实现步骤 ①利用核函数方程计算矩阵K ②对核矩阵K进行中心化 K_n = K - unit*K - K*unit + unit*K*unit; ③对矩阵K进行特征值分解,得到矩阵K的特征值evaltures_1与特征向量evectors_1 ④除以特征值的根号sqrt(evectors(:,i)))并选取主成分 ⑤evecs是单位化后的特征矩阵,K_n是训练数据的中心化核矩阵 将训练数据进行映射 train_kpca=K_n * evecs(:,1:index(1)); 说明:核矩阵K进行中心化的目的是为了使核映射后均值为零。在本次实验中我所采用的核函数是高斯核函数。 4.3线性判断分析LDA 4.3.1 LDA简介 LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。 4.3.2 LDA的matlab实现步骤 ①计算类内散度矩阵Sw ②计算类间散度矩阵Sb ③计算矩阵inv(Sw)Sb ④求inv(Sw)Sb矩阵最大的d个特征值和对应的d个特征向量(w1,w2,…,wd) ⑤对样本内每一个样本特征xi转化成新的样本zi=W*xi 五、降维方法比较分析 5.1 PCA与LDA比较 共同点 降维时均使用了矩阵特征分解的思想 两者都假设数据符合高斯分布 不同点 PCA 无监督 无维数限制 LDA 有监督 最后降维至类别数k-1的维度 除了用于降维,还可以用于分类 另外,LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向,如下图所示。 5.2 PCA与KPCA比较 KPCA与PCA具有本质上的区别:PCA是基于指标的,而KPCA是基于样本的。KPCA不仅适合于解决非线性特征提取问题,而且它还能比PCA提供更多的特征数目和更多的特征质量,因为前者可提供的特征数目与输入样本的数目是相等的,而后者的特征数目仅为输入样本的维数。KPCA的优势是可以最大限度地抽取指标的信息;但是KPCA抽取指标的实际意义不是很明确,计算也比PCA复杂。 六、实验测试结果 我在分别实现每一个算法之后,最后进行了综合,将三种数据降维方法pca、kpca、lda与三种分类方法svm、knn、cnn编写在一个程序中,以便于比较分析各自组合的速度与准确率。程序采用matlab命令行选择数据降维方式与分类方式。具体操作如下图所示: 图10:maltab命令行使用示例 得到的测试结果如下表所示: 数据降维方式 数据分类方式 分类所用时间(s) 测试集准确度 不进行数据降维 CNN 0.127945 95.889% KNN 0.742317 93.556% SVM 0.158921 97.444% LDA KNN 0.187326 96.222% SVM 0.034417 96.000% KPCA KNN 1.574710 92.778% SVM 0.673148 94.889% PCA KNN 0.183935 91.333% SVM 0.077221 96.444% 七、总结 如上表所示,展示了在不同数据降维方式以及分类方法下所需要的时间以及相应测试集的准确度。分类所用时间是统计对900个测试样本总共所需要的时间。可以发现KNN在三种分类分类方式中,计算时间最长,同时其分类效果也是最差的。通过选取合适的降维方法并设置合适的参数,可以大大加快分类速度,并且保持较高的测试集准确度。在上表所展示的方法中,LDA+SVM拥有最快的分类速度,并且保持着较高的分类准确度。PCA+SVM也有着较为出色的表现。相对而言,卷积神经网络CNN在经过反复调参之后,其测试集准确度仍不如SVM,分类算法中SVM在高光谱数据集Paviau分类中有着优秀的表现,而数据降维算法LDA相比于与PCA与KPCA而言,对Paviau降维效果更好。本文主要通过对Paviau高光谱数据集进行分类学习了pca、kpca、lda三种数据降维方法以及svm、knn、cnn三种数据分类算法。通过matlab编程熟悉了解了算法的实现以及原理。 八、代码下载 https://download.csdn.net/download/weixin_37402233/10599005
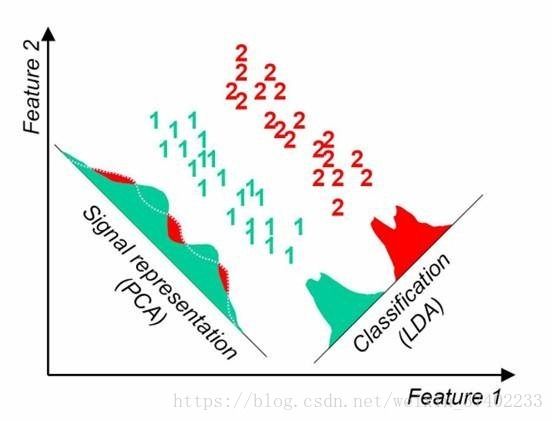
图9:PCA与LDA比较