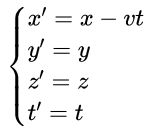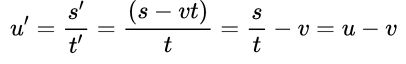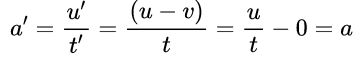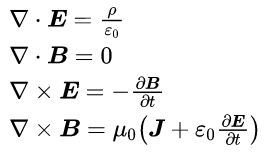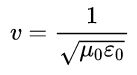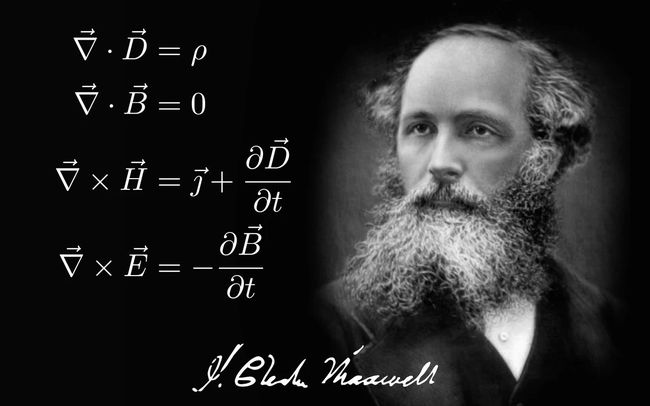为了给狭义相对论作铺垫,我专门写了三篇麦克斯韦方程组的文章,为了让中小学生能更好理解麦克斯韦方程组,我又补了一篇微积分,现在终于可以正式谈狭义相对论了。
为什么讲狭义相对论要先讲电磁理论呢?
爱因斯坦发表狭义相对论的论文叫《论动体的电动力学》,一般电动力学教材的最后一章也会讲狭义相对论。这一来一去,你就知道它们的关系不一般了。
那这跟牛顿又有什么关系呢?
牛顿建立了上知天文下知地理的力学体系,日月星辰、潮起潮落都遵循他的定律,这是第一次工业革命的基石;麦克斯韦方程组则包含了一切经典电磁学的东西,还发现了电磁波,这是第二次工业革命的基础。
牛顿和麦克斯韦的理论在各自领域都获得了巨大的成功,是经典物理学的两座丰碑。但是,如果你试图把它们融合在一起,用统一的目光看待它们,立马就会出现不可调和的矛盾。
为了解决这些矛盾,爱因斯坦进行了艰苦卓绝的探索,并最终创立了狭义相对论。
这种处境,很像现在的广义相对论和量子力学。
当我们使用广义相对论处理引力,处理恒星和宇宙的演化时非常好用(可以忽略量子效应),当我们使用量子力学处理电磁力、强力、弱力时也非常好用(引力太弱,可以忽略)。
但是,当我们碰到那些又重又小的东西,无法忽略引力和量子效应中的任何一个的时候(比如黑洞和宇宙初期的奇点),就必须结合广义相对论和量子力学,这一结合就出大问题了。
广义相对论和量子力学的不兼容是当今物理学一等一的大事,这种情况跟百年前牛顿力学与麦克斯韦电磁学的不兼容很相似。两种理论能够在各自领域工作良好,就证明它们至少包含了某种正确性,而一结合就出问题,说明我们还是忽略了某些关键的东西。
那么,牛顿力学和麦克斯韦电磁学之间的矛盾是什么?为什么它们无法兼容?有什么关键的东西被忽略了,爱因斯坦又是如何发现的?为什么是年轻的爱因斯坦先发现了这个,而那些大物理学家们却老是差那么一点?
类似的,广义相对论和量子力学之间的矛盾又是什么?它们之间被忽略的关键东西又是啥?爱因斯坦统一牛顿力学和麦克斯韦电磁学的工作对我们统一广义相对论和量子力学又有什么启发?
学习历史是为了更好地把握未来,科学也一样。在下面的文章里,我会把尽力历史说清楚,现在和未来的问题,就交给你来慢慢琢磨了~
好,下面进入正题。
01日心说的困境
为了让大家更清楚地了解牛顿和麦克斯韦这两位大神的战争,我们先把时间往前推两千年。没错,又来到了古希腊。
提到日心说,绝大部分人立马就会想到哥白尼,甚至直接把日心说和哥白尼画上等号。但是,如果你去翻翻历史,就会发现早在公元前3世纪,一个叫阿利斯塔克的人就提出了日心说,这比哥白尼早了足足一千八百年。
阿利斯塔克被称为古希腊第一个著名的天文学家,他用数学计算出太阳的半径比地球大很多(虽然不够精确)。所以,他认为是太阳在宇宙中心,地球围着太阳转,地球自转一圈为一天,地球围着太阳公转一圈为一年。
这是一个很强的论证,如果太阳真的比地球大很多,我们当然更倾向于认为是小地球围着大太阳转。此外,他还发明了一些方法去测量太阳、月亮和地球之间距离的比值。
虽然受限于条件,他当时没法测得很准,但是随着时间的推移,这些数据肯定是会越来越精确的,那得到的结果也应该越来越支持阿利斯塔克的日心说。
但是,后面的结果我们都知道了。400年后,古代欧洲最伟大的天文学家托勒密在构建他的天文体系时采用的是地心说,而不是日心说,为什么?
抛开教会支持地心说不谈,托勒密作为一位杰出的科学家,他为什么最终选择了地心说,而不是看起来很合理的日心说呢?
具体的原因有很多,但其中有一条影响非常大,绝对不容忽视,甚至可以说是击中了当时日心说死穴的原因:如果地球真的在高速转动,那为什么我们跳起来后会落回原地,而没有被甩出去?为什么天上的云不会被吹向一边?
这个问题放到现在当然很简单,一个初中生都可以自豪地甩出“惯性”送给你。但是在当时,或者说在伽利略以前,这都是巨大的科学难题。
当我们在说惯性的时候,我们其实已经默认了伽利略-牛顿的运动观,认为“力是改变物体运动的原因,而不是维持运动的原因”。
但伽利略之前的人并不知道这些,他们认为运动是需要力来维持的。你跳起来之后没有力了,但是依然能落回原地,那就只能说明地球是静止的。
于是,托勒密就理所当然地拒绝了日心说!
02相对性原理
解决这个问题的人是伽利略。
伽利略想,这里的核心问题就是要解释“为什么地球在动,但是我却感觉不到地球在动?”。这个问题并不难,地球太大了不好说,我们先来看看我们熟悉的船。
假设在一个平静的湖面上有一艘匀速直线行驶的大船。我把所有的窗户都关上,让乘客看不到外面的景象。那么,乘客能根据船舱里的情况分辨出这艘船是静止还是匀速直线运动的么?
答案是不能!
你可以在船舱里做各种实验:你可以跳起来,然后发现自己会落回原地;你去看鱼缸的鱼,发现鱼依然均匀地分布在鱼缸的各个部分,并不会挤向船尾的方向;你可以跟朋友正常地玩篮球,而不用担心篮球会往后窜。
总之,大家可以想象,你在这个匀速行驶(一定要是匀速,加速的话就能明显感觉到不一样了)的船舱里做的一切力学实验,都应该跟在静止的船舱里没有任何区别。
也就是说,我们根本无法通过力学实验区分这艘船是静止的还是匀速直线运动的,这就是伽利略的相对性原理。
相对性原理告诉我们,一个静止和匀速直线运动的参考系是完全等价的。我们无法通过力学实验区分二者,这也非常符合我们的生活经验。
飞机在天上平稳飞行的时候,你可以在飞机里看书、写作,就像在家里一样。如果不看窗外的景象,你也很难区分飞机是在飞行途中还是静止在机场。一座在匀速上升或者下降的电梯,你会感觉它跟没动一样,只有电梯在加速减速的时候,你会发现明显的不同。
其它例子我就不多举了,相信大家只要稍微想一想,就会明白相对性原理其实是非常自然的。
有了相对性原理,日心说的困境就迎刃而解了,为什么?
因为我完全可以认为地球就是这样一艘大船(大飞机),它非常均匀的运动。所以,你根本就不能通过“跳起来会落回原地”这个事实来证明地球是静止还是运动。静止的地球会有这样的结果,匀速运动的地球一样会有这样的结果。因此,就算我支持日心说,认为地球在高速转动,这个事实也不会跟日心说发生冲突了。
于是,攻击日心说最锋利的武器瞬间就变成了一堆废铁。有了伽利略的这波神助攻,哥白尼的日心说才没有在这里翻车。
03惯性系
好,现在我们知道了:静止和匀速直线运动的参考系等价的,或者说惯性系都是等价的。
什么是惯性系?
惯性系的定义是个比较麻烦的问题,有些书用“满足牛顿第一定律的参考系”来定义惯性系。也就是说,如果一个物体在不受外力(或者合外力为零)的情况下能保持静止或者匀速直线运动,那它所在的参考系就是惯性系。因此,牛顿第一定律又叫惯性定律。
但是,如果深究一下,你就会发现这里出现了循环定义,因为什么叫不受外力?你想来想去,最后只能用“在惯性系里保持静止或者匀速直线运动”来定义不受外力。
这样,你定义惯性系需要依赖不受外力这个概念,定义不受外力又要依赖惯性系,这就是典型的循环定义了,这在逻辑上是不允许的。
不过,虽然逻辑上有点问题,但日常使用起来还是很方便的。你把一个篮球放在地面上,这个篮球静止不动,所以地面系就可以看作一个惯性系;你把这个篮球放在一辆加速的汽车上,篮球会向车尾滚动,所以加速的汽车系不是惯性系。
关于惯性系的定义,这里就不做深入讨论了。如果大家感兴趣,后面我可以专门写文章讨论这个麻烦的问题。
在这里,我们只要知道地面系可以近似看作惯性系,而且,如果一个参考系相对某个惯性系做匀速直线运动(比如一辆匀速运动的火车),那么这个参考系也是惯性系就行了。
有了惯性系的概念,伽利略的相对性原理就可以简单的说成“力学实验对所有的惯性系都平权”,或者说“我们无法通过任何力学实验来区分两个惯性系”,就不用老是重复说静止和匀速直线运动了。
毕竟,你在地面上觉得地面静止,火车在匀速运动;你在火车上,又会觉得火车静止,地面上的东西在匀速运动。静止和运动是个相对的概念,它取决于你如何选择参考系。
所以,执着于区分静止和匀速直线运动是没啥意义的,我们只要把握住它们(地面系和火车系)都是惯性系,而力学实验无法区分惯性系就行了。
好,我们现在知道了相对性原理要求力学实验对所有的惯性系都平权,而力学实验是由对应的力学定律来描述的。那么,相对性原理会对这些力学定律做出什么样的要求呢?
想找到答案,我们需要对相对性原理做更深层次的剖析。
04从实验到定律
假设现在有地面系和火车系两个惯性系,火车相对地面作匀速直线运动。
当我们说力学实验无法区分地面系和火车系的时候,我们是在说:我在火车里抛球也好,跳远也好,做的各种力学实验跟在地面上的感觉都是一样的。
你在地面上能跳多远,在火车上就能跳多远;你在地面上从1米高的地方放一个小球,这个小球经过多长时间着地,在火车上小球也会经过同样的时间着地。
你觉得不管在地面还是火车,1米高的小球都会经过相同的时间落地,所以我无法通过这个区分地面系和火车系。但是,这个下落时间,我们是可以通过力学定律精确算出来的。
比如,我们使用牛顿力学(当然你也可以用其它的理论,比如广义相对论)的自由落体运动公式,很快就能算出这个下落时间大概是0.45秒。
也就是说,你在地面系使用牛顿运动定律计算小球下落,得到的时间是0.45秒;在火车系依然使用这个公式计算,得到的结果依然还是0.45秒。
正因为你在地面系和火车系计算的时间都一样(废话,一样的公式,一样的已知条件,结果不一样才见鬼了~),你才会无法区分这两个惯性系。
不过,不知道你意识到了没有,你在这个过程中使用了一个可能连你自己都没有意识到的假定。正是这个假定,保证了你在地面系和火车系的计算结果都一样,保证了你无法区分这两个惯性系,保证了相对性原理。
这个假定就是:你默认牛顿运动定律不管在地面系还是火车系都是长这样的,你用来计算小球下落的数学公式,不管在地面系还是火车系都一样。
正因为你在地面和火车使用的都是这个公式(H=gt²/2),所以算出来的时间才会一样。你想想,如果你在地面系用H=gt²/2去算,在火车系用H=gt²/3去算,那结果还能一样么?
我知道,肯定有些人觉得我这是废话。牛顿运动定律只此一家,别无分店,怎么可能一个公式在地面系长这样,在火车系长那样呢?
我们学习自由落体运动的时候,老师也只讲了这一个公式,不管地面系还是火车系,你用得用它,不用还得用它,因为你压根就没有别的选择。
对对对,你说的都对,所以我才说很多人平常都不会意识到这个事情。
但是,你不得不承认这个问题确实是存在的。而且,正因为牛顿运动定律在地面系和火车系的数学形式一样,你才无法区分地面系和火车系,才会符合相对性原理。更重要的是,这并不是一件多么理所当然的事。
你觉得物理定律的数学形式在不同的惯性系里就必须长一样么?不不不,你有严格地证明么?你只不过觉得应该是这样的,然后就默认这样用了,而牛顿力学刚好满足这个条件罢了。
我完全可以认为某些定律只能在某些特殊的惯性系里使用,在其它的惯性系里使用就是错误的。这样,在不同的惯性系里使用定律的数学形式就不一样了,那么你就能区分这两个惯性系了,这也就意味着相对性原理不再成立。
所以,物理定律的数学形式在不同惯性系里是否一样,要看它是否满足相对性原理。这绝不是理所当然,天生就成立的。
也就是说,从实验的角度来看,相对性原理要求力学实验对所有的惯性系平权。你不管在哪个惯性系里做力学实验,你的感觉应该都是一样的,这样才无法区分这两个惯性系,它们才平权。
从定律的角度来看,相对性原理要求力学定律在所有惯性系的数学形式都一样。因为只有定律的数学形式一样,它在不同惯性系计算的结果才一样,这样才能“欺骗”你的感觉,让你无法分辨出在哪个惯性系,这样惯性系才平权。
从实验到定律,这两种表述是等价的,都是相对性原理的体现。
那么,牛顿力学是否满足相对性原理呢?应该是满足的。不然你在火车、飞机上使用了这么久的牛顿运动定律怎么一直没有出错呢?那要如何证明?如何证明牛顿运动定律的数学形式在所有的惯性系里都一样?
以前我们可能不知道有这回事,拿着牛顿的定律在地面系、火车系、飞机系随便就用。现在知道了,那就肯定要找一找这么做的合法性依据在哪,不能再继续这样耍流氓下去了。
以牛顿第二定律F=ma为例,假设它在地面系是这样的,那我要怎么证明它在火车系还是这样的呢?
你会发现我们需要一个桥梁,一个沟通地面系和火车系的桥梁,一个能把牛顿第二定律从地面系变换到火车系的桥梁。看看我们把F=ma变换到火车系之后,它的数学形式到底还是不是这样。
那地面系和火车系之间有没有桥梁呢?当然有,因为它们本身就有关系。
火车在地面上以一定的速度匀速运动,同一个事件,地面系把它的信息记录了一份,火车系也把它的信息记录了一份,这两者肯定是有某种关系的。
我们要做的,就是把这种变换关系找出来,把这两个惯性系之间的关系找出来,然后再看看牛顿力学的定律在这种变换下的数学形式是否发生改变。
那么,这到底是什么样的一种变换呢?
05伽利略变换
牛顿力学非常符合常识,所以这种变换应该也是符合常识的,我们不妨先来猜一猜。
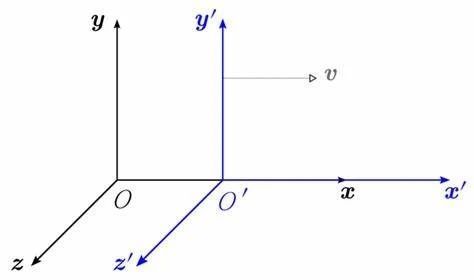
假设我们在地面系S建立一个坐标系(x,y,z,t),有一辆火车以速度v(沿x轴正方向)匀速运动,我们在火车系S’里也建一个坐标系(x’,y’,z’,t’)。为了简化问题,我们让这两个坐标系一开始是重合的。
对于任何发生的事件,地面系和火车系都会记录下事件发时空信息(x,y,z记录空间信息,t记录时间信息)。我们想要知道的就是:这两套坐标系记录的时空信息之间有什么关系?
先看时间。
假如火车上有一个小球开始下落,火车上的时钟记录的时间为八点,那地面上的时钟会觉得是几点呢?不要笑,我不是在逗你玩,我是在讨论一件很严肃的事情~
你可能会觉得这还需要讨论么?
火车上的时钟记录的时间是早上八点,地面的钟只要没坏,不考虑什么时区的问题,它当然也是早上八点。
不仅如此,所有的钟记录的时间应该都是一样的,这是生活常识。我们宣布奥运会什么时候举行,只需要对外公布一个时间。不会说北京时间什么时候,上海时间什么时候,更不会说高铁时间什么时候,因为我们默认大家都共用一个时间:同一个世界,同一个时间。
没错,这种认为是非常有道理的,也非常符合我们的常识。
我不会说你这种想法是对还是错,我只能说这代表了你对时空的一种看法,这是你的一种时空观。在这种时空观下,时间是绝对的,独一无二的,所有人都共用同一个时间。
也就是说,如果你认同这种绝对的时间观,那么火车系测量时间t’和地面系测量时间t就应该永远都是相等的,即t’=t。
到后面我们会发现,这个问题绝不是你想象的这么简单,它背后大有学问。越是符合常识,越是平凡的东西,想要发现它的不平凡就越不容易。
好,接下来看空间。
地面系和火车系的三个空间坐标x,y,z应该满足什么关系呢?因为火车只沿着x轴运动,所以,你在地面系和火车系测量的y和z的值应该也是一样的(即y’=y,z’=z),唯一不同的就是x了。
这个关系也不难,大家琢磨一下就能得到这个结果:x'=x-vt。
也就是说,如果地面系测量的横坐标是x,你用这个x减去vt(火车的速度v乘以时间t),就能得到火车系下测量的横坐标x’。
你可以自己比划一下,假如你在火车系的原点处放一个小球,那么这个小球在火车系的横坐标x’就永远等于0(x’=0)。火车的速度乘以时间vt刚好就是地面系测量的它的位移x,这代入(0=x-vt)进去刚刚好。
如果小球不在原点,不难验证它们的横坐标依然满足这个关系。于是,我们就找到了两个惯性系之间的坐标变换关系:
如果我在地面系S观测到一个事件的时空坐标为(x,y,z,t),通过上面的坐标变换公式就能求出它在速度为v的火车系S’上的坐标(x’,y’,z’,t’),这样我们就找到了联系两个惯性系之间的一座桥梁。
回想一下,这种变换之所以能成立,是因为我们假设时间是绝对的(t’=t,它在所有参考系里都是一样的),空间像一个坚固的大盒子,无法被压缩。在这种绝对的时空观下,我们推出了两个惯性系之间的坐标变换关系,这个变换就叫伽利略变换。
06牛顿力学与伽利略变换
而牛顿力学也是绝对的时空观,牛顿在《自然哲学的数学原理》的一开头就写到:绝对的、真实的、数学的时间,由其特性决定,自身均匀的流逝,与一切外在事物无关;绝对空间自身的特性与一切外在事物无关,处处均匀,永不移动。
既然牛顿力学是绝对的时空观,而我们从绝对时空观里又自然地推导出了伽利略变换。那么,不难想象,在牛顿力学里联系两个惯性系的坐标变换应该就是伽利略变换。
也就是说,如果牛顿力学满足相对性原理,那么牛顿力学的所有定律就应该在伽利略变换下保持数学形式不变。
如果一个定律在地面系是A=BC,这几个量经过伽利略变换后变成了火车系的A’、B’和C’,那么它们还应该满足A’=B’C’,这样才叫数学形式没变。
我们说牛顿力学的定律形式不变,并不是说它什么都不变。物理量A、B、C经过伽利略变换之后变成了A’、B’、C’,那肯定跟以前的量不一样了。但是,你一个量变了,大家协同着一起变,最后总的数学形式依然保持A’=B’C’这个样子,这才是牛顿力学的所有定律在伽利略变换下保持形式不变的真正意思。
因此,我们也可以说牛顿运动定律具有伽利略协变性,或者伽利略不变性(在伽利略变换下所有物理量都协同变换,但是总的形式保持不变),用协变性、不变性大家可能更容易理解一些。
这段逻辑大家一定要好好理清楚,只有把这段彻底搞清楚了,才算真正明白了相对性原理。
为了让大家更深刻地理解“牛顿运动定律具有伽利略不变性”,我们来看一个具体的例子,看看大名鼎鼎的牛顿第二定律(F=ma)是如何具有伽利略不变性的。
07牛顿第二定律
牛顿第二定律说一个物体受到的合外力F等于这个物体的质量m乘以加速度a(F=ma),那我们就来分别考察一下这三个量在地面系和火车系的情况。
先说质量m,质量是一个不变量。不变量就说它是不随参考系的变化而变化的,你在地面系测的值是多少,在火车系就还是多少。
这个比较容易理解,质量是物体的一个内在属性,它怎么可能随着参考系的变化而变化呢?比如你去查电子的质量,那就是一个具体的数字(9.10956×10^-31kg千克),白纸黑字地写在那里,是不会随参考系的变化而变化的。
在牛顿力学里,除了质量m,力F也是一个不变量。这就是说,对地面系和火车系来说有m’=m,F’=F,那问题的关键就是看加速度a’和a了。
地面系和火车系的加速度有什么关系呢?
我们可以这样看,加速度是单位时间内速度的变化,速度是单位时间内位移的变化,而火车系S’和地面系S的位移关系是伽利略变换直接给出的(x’=x-vt)。那么,我们把位移关系的两边同时除以两次单位时间,不就能得到加速度a’和a的关系了么(用微积分说就是对时间求两次导数)?
好,火车系的速度是u’=s‘/t’,地面系的速度是u=s/t,我们把x’=x-vt的两边都除以时间(因为伽利略变换里t=t’,所以两边可以分别除),然后对应的速度关系就简单了(因为火车只沿x轴方向的运动,所以x和位移s是相等的,写成s’=s-vt也没问题):
推导很简单,得到的结果u’=u-v就是我们熟悉的速度合成法则,也就是说这两个惯性系测量的速度相差一个速度v,符合题意,没毛病。
好,有了速度关系u’=u-v,我们两边再同时除以一次单位时间,就能得到加速度a’和a的关系:
因为速度v是参考系的相对速度,是一个不随时间变化的常数,所以它在单位时间的变化量就是0,于是就对加速度就没有影响了。所以,我们就得到了a’=a,也就是说火车系的加速度a’等于地面系的加速度a。
这样,我们就发现地面系和火车系的力F、质量m和加速度a都是相等的(F’=F,m’=m, a’=a)。那么,如果牛顿第二定律在地面系长F=ma这样,经过伽利略变换之后的F’、m’、a’就依然可以满足F’=m’a’。
这就意味着牛顿第二定律的数学形式在伽利略变换前后保持不变,因此它具有伽利略不变性,证毕。
当然,不只是牛顿第二定律,牛顿力学的所有定律都具有伽利略不变性,你可以仿照我这个思路去验证一下。
08绝对时空观
好,到了这里,我帮大家把前面的思路理一下:伽利略为了给日心说做辩护,从生活经验和实验中提炼出来了相对性原理。
它告诉我们,无法通过力学实验区分静止和匀速直线运动的参考系,所有的惯性系都是平权的,没有谁更特殊。
力学实验由对应的力学定律(比如牛顿运动定律)来描述,如果一套理论满足相对性原理,那么它的数学形式就应该在所有的惯性系里保持一样。
为了验证一个定律在不同的惯性系的数学形式是否一样,我们就需要找到联系两个惯性系的桥梁,这就是坐标变换。而变换并不是天然存在的,不同惯性系下的物理量之间有什么关系,这严重依赖于你的时空观。
比如,你觉得所有惯性系测量的时间都是一样的吗?如果你回答是,那就说明你认为时间是绝对的,认为全世界的观察者都共用一个时钟。你觉得空间是像一个坚固的大房子,还是像一块可以被压缩拉伸的海绵?不同的回答就意味着对空间的不同理解。
不难想象,对时间和空间的不同理解,必然会导致不同的变换。
牛顿力学是绝对的时空观,它认为时间均匀流逝,与一切外在事物无关;空间处处均匀,永不移动。这种绝对时空观对应的变换就是伽利略变换,而牛顿力学的所有定律在伽利略变换下能够保持数学形式不变,所以牛顿力学满足相对性原理。
在绝对时空的大背景下,牛顿力学和伽利略变换配合得天衣无缝。它们能解释苹果下落,气球上升,能解释潮起潮落,也能解释日月星辰的轨道。力学取得了空前的成功,牛顿直接封神。
后来,人们把这种力学思想运用到热现象里去,把宏观的热现象还原成了微观分子间的相互作用,建立了热力学,一样获得了巨大的成功。
但是,当人们把研究对象转向电磁领域的时候,上帝的天平不再偏向牛顿和伽利略,电磁定律把他们组建的世界冲得七零八落。
大家都知道经典电磁领域的集大成者是麦克斯韦方程组,为了给这篇文章做准备,我前面专门写了三篇麦克斯韦方程组的入门文章(积分篇、微分篇和电磁波篇),这里就不再详述了。
电磁理论,或者说麦克斯韦方程组有什么问题呢?
09电磁理论的挑战
用一句话说就是:电磁定律不再满足伽利略变换,麦克斯韦方程组不具有伽利略不变性。
也就是说,麦克斯韦方程组长这样:
如果我们用伽利略变换把方程组的各个物理量都映射到另一个惯性系S’里,那么,在S’系下的新物理量将不再满足上面这种关系。
这跟牛顿第二定律完全不一样。上面我们已经验证了,我们把牛顿第二定律F=ma用伽利略变换从一个惯性系映射到另一个惯性系,新系下的F’、m’、a’依然能组成牛顿第二定律F’=m’a’,而麦克斯韦方程组办不到。
麦克斯韦方程组不具有伽利略不变性,这个事情既不需要实验验证,也不需要什么额外的假设。因为方程组就长这样,伽利略变换也是明确给出的,你判断麦克斯韦方程组是否具有伽利略不变性,这是一个纯粹的数学问题。你一通计算之后,它满足就满足,不满足就是不满足,没有讨价还价的余地。
所以,面对麦克斯韦方程组不具有伽利略不变性这个既定事实,我们要考虑的是:为什么会这样?
牛顿力学满足相对性原理,它用代表绝对时空观的伽利略变换与之适配。
现在麦克斯韦方程组跟伽利略变换不适配,那么就应该有两种可能:第一,麦克斯韦方程组根本就不满足相对性原理;第二,麦克斯韦方程组虽然满足相对性原理,但是与之适配的变换并不是伽利略变换。
那么到底是哪一种情况呢?我们来逐一分析下这两种可能性。
10第一种可能
如果是第一种,也就是认为麦克斯韦方程组不满足相对性原理,那是什么意思呢?
不满足相对性原理,就是说麦克斯韦方程组的数学形式并不是在所有的惯性系里都一样,它可能只在某个惯性系长这样,在其它的惯性系里就不是这样的了。假如麦克斯韦方程组在地面系是这样的,那么你可以在地面用它处理电磁现象,在火车系就不行了。
你可能觉得这太荒谬了,怎么可能我在火车上就不能使用麦克斯韦方程组了呢?难道火车上的电磁现象就不满足这些规律?如果法拉第在火车上做实验,会得出与实验室里完全不一样的电磁定律出来么?
荒谬归荒谬,但是如果你认为麦克斯韦方程组不满足相对性原理,结果就是这样。
当然,如果你认为麦克斯韦方程组在火车系不能用,那么我们也没有理由认为它在地面系就能用。因为地球只不过是宇宙里极其平常的一个星球,如果麦克斯韦方程组只在一个参考系中成立,那凭什么是地面系?太阳系可不可以?火星系可不可以?
所以,如果你非要认为麦克斯韦方程组不满足相对性原理,它只在一个参考系适用。那么,我们就只能选择一个在宇宙范围内看起来非常特殊的参考系,那这个参考系是什么呢?
很容易想到,如果我们秉持牛顿-伽利略的绝对时空观,把整个空间都看作一个坚固的大房子,那么这个房子本身所在的参考系毫无疑问就是那个最特殊的参考系。
另一方面,麦克斯韦方程组认为光是一种电磁波,传统的波动说认为只要是波那就一定有介质,没有介质波怎么传播呢?水波的介质就是水,声波的介质就是空气,没有水自然就没有水波,在真空里也听不到声音。
而光是一种电磁波,那么我们自然也需要一种能够传递电磁波的介质。
于是,我们会发现,要让假设成立,我们需要一个空间这个大房子本身所在的特殊参考系,这个参考系还要能够作为传播电磁波的介质。由于光可以在真空中传播,我们在宇宙的各个方向都能看到光,所以这种介质还应该遍布宇宙。
所以,大家就假设有一种铺满宇宙的东西,它既是那个最特殊的参考系,也是电磁波的介质,它的名字就叫以太。
大家可以发现,如果我们假设麦克斯韦方程组不满足相对性原理,那以太的出现几乎就是必然的,而且还跟我们熟悉的绝对时空观不冲突,多好!
这样处理的代价似乎是最小的,麦克斯韦本人接受的也是这样的观念。
也就是认为宇宙中充满了轻盈的以太,光通过以太传播,麦克斯韦方程组只能在以太系中成立,在其他参考系里不成立,所以它不满足伽利略变换也是说得过去的。
那么,为什么我们在地球上使用麦克斯韦方程组却没有出错呢?难道这么巧,地球所在的参考系刚好就是以太系?或者说,地球因为某种原因带着以太一起运动?不能够吧,这也太巧了,比你在1998年去杭州跟一个叫马云的人拜了把子的概率还小。
所以,物理学家们就只能拼了命的去寻找以太。如果地球真的“浸泡”在以太池里,那么地球自转的时候多多少少会产生一些“以太风”,只要实验设计得足够精巧,我们理论上是能找到它的。
然而,实验并没有找到任何以太风,事情就这样尴尬地僵住了。
11第二种可能
这样,第一种情况就分析完了,我们再来看看第二种情况。
也就是我们认为麦克斯韦方程组依然满足相对性原理,只不过,与之适配的变换并不是伽利略变换。
为什么我们要考虑第二种情况呢?是因为第一种情况会导致以太,但是大家死活都找不到以太,所以转向第二种么?
是,也不是!
大家找不到以太,当然会慢慢降低第一种可能性的威信,于是转而考虑第二种是可以理解的。但是,这个原因并没有那么重要,因为你找不到以太,大家还可以给你解释为什么你找不到以太(参见洛伦兹的操作,他用长度收缩来解释为什么我们观测不到以太风),不会轻易放弃,转而“投敌”的。
为什么要考虑第二种情况,因为第二种情况本身就很值得考虑。
相对性原理是个多么美妙的原理啊,伽利略当年就是凭着它给日心说翻盘的。牛顿力学的大获成功,就已经证明了相对性原理在力学领域是非常正确的,那凭什么到了电磁领域就不正确了呢?
在一个匀速直线运动的船舱里,我无法通过力学实验分辨出这艘船到底是静止还是匀速运动,难道通过电磁实验就能够区分了?
难道在匀速直线运动的船舱里,我们的电磁定律都不一样,那么我们使用的各种电气电子设备岂不是都要出问题了?如果我们的手机在运动的火车里不能用,你觉得这可能吗?
如果你坚持认为电磁定律不满足相对性原理,那么,上帝除了要制造一个特殊的以太参考系,还要让有的定律(力学定律)满足相对性原理,有的定律(电磁定律)不满足相对性原理,他不嫌麻烦么?他制造了这样一个又复杂又不美的体系,他妈妈知道么?
很多物理学家对物理定律的简单和美都有一种执着的追求,爱因斯坦、狄拉克、杨振宁都是这样,而相对性原理就是这样一条又简单又美的原理。
所以,不管是从美学考虑,还是从哲学考虑,让电磁定律放弃相对性原理都是让人很难接受的一件事。更何况,你根本没有任何实验证据,那就更可疑了。
近代物理学的发展,就是一部人类特权的消亡史。最开始你认为地球是宇宙中心,结果发现地球只不过是太阳系的一颗普通行星;你以为太阳是中心,结果发现银河系里有无数个太阳系;当你准备站银河系的时候,大量河外星系被发现了。当你准备退一万步,说起码这个宇宙是唯一的吧,结果很多理论都指向了各种版本的平行宇宙。
你以为你很特殊,结果物理学一次次告诉你:你一点也不特殊,上帝好像也没有倒腾什么特殊的东西。
既然这样,既然上帝这么公平公正,为什么我们要相信他预设了一个特殊的参考系呢?为什么他会对电磁定律开特殊的后门呢?相对性原理说大家都绝对公平,所有的惯性系都一样,这很符合近代物理的精神啊。
所以,我们也有充分的理由认为麦克斯韦方程组也是服从相对性原理的。
如果麦克斯韦方程组服从相对性原理,而它却不具有伽利略不变性,那我们就只能认为跟麦克斯韦方程组适配的变换并不是伽利略变换了,这又意味着什么呢?
12新的时空观
前面我也说了,伽利略变换是绝对时空观的体现,只要你假设大家都共用一个时间,认为空间就像坚固的大房子那样,那么惯性系之间的变换关系就是伽利略变换。
如果你认为麦克斯韦方程组不满足伽利略变换,那这就是在挑战绝对的时空观,这就是翻天的大事了。
所以,一般人根本就不敢往这方面想。虽然大家都认为相对性原理很美妙,觉得如果电磁理论也满足相对性原理,那当然是非常不错的事情。
但是,当他们继续往前走,发现这会跟绝对时空观发生冲突时,他们就立马起身告辞,表示下次一定支持相对性原理,然后就继续寻找以太去了。
为什么当相对性原理跟时空观发生冲突时,绝大部分人都立马抛弃了看起来很美的相对性原理,而选择坚守时空观呢?
这个其实也很容易理解。首先,很多人压根就没意识到有时空观这个问题。当他们发现如果让麦克斯韦方程组满足相对性原理,就会出现一些“荒谬”结论的时候,他们就觉得这是一条死路,这是方向错了,不予考虑。
然后,有极少数非常优秀的科学家会意识到这个问题。他们会隐隐约约地感觉到:“麦克斯韦方程组没问题,相对性原理也没问题,那是不是牛顿-伽利略的绝对时空观有什么问题?时间和空间是不是有可能并不是这样的?”
但是,光怀疑是不够的,你说绝对时空观可能不对,那么正确的时空观是什么?如何在全新的时空观里建立全新的物理学?摧毁旧世界是容易的,难的是如何建立新世界。
最后,只有一个年轻的科学家敢于完全抛弃绝对的时空观,并且在全新的时空观下建立了全新的物理学,彻底跟旧世界决裂。
因为他年轻,没有思想包袱,所以在旧世界里陷得不深,所以敢直接放弃旧的时空观。
因为从小就读康德、休谟、马赫、庞加莱等哲学大师的著作,所以不论是从哲学还是美学考虑,他都无比钟爱相对性原理。
因为他思考问题思考得很深,所以能找到让麦克斯韦方程组和相对性原理共存的办法。
因为他生活在钟表大国瑞士,供职于专利局,每天都要审查非常多跟时间钟表相关的专利,所以他对时间问题特别敏感,并最终从时间这里找到了关键的突破口。
这个人是谁,我相信你们都知道,他就是爱因斯坦。
只要把麦克斯韦方程组和相对性原理之间的冲突解决了,狭义相对论的诞生就是水到渠成的事了。
至于爱因斯坦是如何着手解决这个问题,他又是如何发现问题的关键,解开了别人眼里的死结从而创狭义相对论的,我下一篇文章再细说。
这里,我再带大家看一个具体的例子。看看如果坚持麦克斯韦方程组和相对性原理,到底会出现什么“大逆不道”的结论,以至于把那么多科学家都直接吓跑了。
13电磁波的疑难
在我的麦克斯韦方程组的第三篇文章《见证奇迹的时刻:如何从麦克斯韦方程组推出电磁波?》里,我带着大家一步步从麦克斯韦方程组推出了电磁波的波动方程,并给出了电磁波的速度公式:
因为μ0、ε0都是常数,代入进去我们就会发现电磁波的速度等于光速,从而发现“光是一种电磁波”。
对于能看到这里的朋友,我相信对这个结论已经不会奇怪了,那么真正奇怪的地方在哪里呢?
大家再去看看电磁波的推导过程,你会发现一件奇怪的事情:我是直接从麦克斯韦方程组出发,一顿数学操作之后得到的电磁波速度公式。整个过程我没有预设任何物理上的东西,没有预设任何参考系!
可能你还没有意识到这件事情的怪异之处,那我们再来回忆一下。初中刚学物理的时候,老师就一定跟你强调过:速度是相对的,你在说一个物体的速度的时候,一定要指定参考系,否则你说的速度就是没有意义的。
你坐在家里觉得自己没动,但是你相对太阳就在高速运动;你觉得地面的树没动,但是火车上的人就会觉得树在高速运动。这些很好理解,大家也很容易接受“凡谈论速度,必先指定参考系”。
但是,你在计算电磁波速度的时候,你指定参考系了么?你选定了哪个特定的参考系了么?
没有,都没有!
你做的事情就是拿起麦克斯韦方程组,一顿操作猛如虎,一通纯数学计算之后得到了那个电磁波的速度公式。
你在没有指定任何物理情景,没有指定任何参考系的情况下算出来了一个电磁波速度,那么这个速度算谁的?
地球系的?火车系的?太阳系的?显然都没有道理!
但是我们就是凭空算出一个速度c来了,虽然我不知道这是相对哪个参考系的,就像石头缝里凭空冒出一个孙猴子一样。
遇到这样棘手的问题,你会怎么考虑?
很显然,你没有任何理由认为这个速度是相对哪个具体参考系的,地球不行,火车不行,太阳也不行。
那么,要么你就认为存在一个特殊的参考系,比如我们在第一种可能里说的以太,认为这个速度是相对以太的。这其实就是认为麦克斯韦方程组不满足相对性原理。
要么,你就认为这个速度对所有的惯性系都成立,也就是认为电磁波在所有惯性系下的速度都是c。这其实就是认为麦克斯韦方程组满足相对性原理,认为它在所有的惯性系下都是正确的,这就是前面讨论的第二种可能。
从这里也可以看出,即便我们不从相对性原理本身考虑,麦克斯韦方程组推出的这个电磁波速度也逼着你不得不二选一。麦克斯韦方程组是否满足相对性原理,这是一个必须回答的问题。
此外,很多科普文章说,因为麦克斯韦方程组推出电磁波的速度(也就是光速)是一个常数,所以我们可以从麦克斯韦方程组推出狭义相对论的光速不变原理,这是不对的。
14光速不变原理
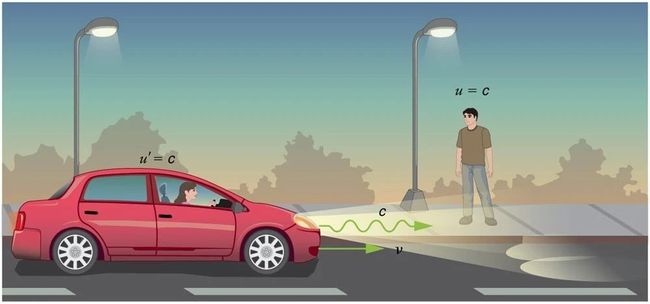
光速不变原理不是说光在真空中的速度是一个定值(我声波在空气中的速度还是一个定值呢),而是说你不管在哪个惯性系里测量真空中的光速,它都是一个定值。
它的重点是强调真空光速在所有的惯性系里都一样,也就是说真空光速对所有惯性系都平权。
大家能看到这里来,这句话已经听熟了吧?所有的惯性系都平权,这不就是相对性原理的核心思想么?
所以,你单从麦克斯韦方程组推出的电磁波速度,是无法推出光速不变原理的,因为这个速度根本就没有提及任何参考系。我完全可以说麦克斯韦方程组推出的光速只在以太系里成立,在其它系里不成立,这样你还能说光速不变么?
但是,如果你同时坚持麦克斯韦方程组和相对性原理,认为方程组在所有的惯性系里都成立。那么,你就可以在所有的惯性系里推出电磁波的速度,这样你就可以说真空光速在所有的惯性系里都是不变的,这才是光速不变原理。
也就是说,单独的麦克斯韦方程组推不出光速不变原理,但是麦克斯韦方程组+相对性原理就能推出光速不变原理。
所以,问题的核心还是你要不要坚持相对性原理。
而“真空光速在所有惯性系里都不变”这样一个结论对牛顿力学,对绝对时空观有多么“大逆不道”,大家应该能感觉到吧。
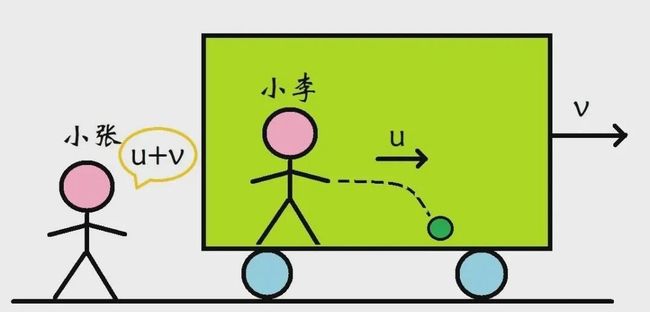
它直接颠覆了我们熟知的速度合成法则。我在地面观测火车上物体的运动速度,那肯定是要把火车的速度和物体的运动速度叠加起来考虑的,怎么可能我在火车上观察这个物体是这个速度,在地面上观察还是这个速度呢?
举个例子,在时速300km/h的高铁上,有一个列车员以5km/h的速度朝车头走去。火车上的人觉得列车员的速度的5km/h,地面上的人自然觉得列车员的速度是300+5=305km/h。
这时候如果有个人跳出来说,不对,我在地面看到这个列车员的速度跟在火车上看到的一样,都是5km/h,那估计大家要送你去精神病院了。
但是,当我们把这个列车员换成了一束光,结论就变成这样了。火车和地面的人竟然都觉得这束光的速度是c,你说这结果可怕不可怕?
而我们所做的,仅仅是假设麦克斯韦方程组满足相对性原理,然后光速就被吓得不敢变了!这种“大逆不道”的结论,牛顿和伽利略当然要不起,这基本上是要掀他们的桌子了。
所以,我们再来看看这个直击灵魂的问题:麦克斯韦方程组到底满不满足相对性原理?
15结语
至此,狭义相对论诞生前夜的各种素材,我都已经帮你准备好了。牛顿力学、麦克斯韦方程组、相对性原理、伽利略变换、绝对时空观之间的关系,我也基本上给你理清了。
有的朋友可能还会有点疑问:别的书籍文章在讲狭义相对论之前,都要大讲特讲迈克尔逊-莫雷实验,然后从这个实验出发讲光速不变,怎么你这里一句都没提?
你去翻一翻爱因斯坦的论文《论动体的电动力学》(后台回复“狭义相对论论文”),里面一样一句没提迈克尔逊-莫雷实验。
爱因斯坦是从电磁学出发建立的狭义相对论,因为他的叔叔是电气工程师,他们家又开了一个电气工厂,所以爱因斯坦从小就对电磁学非常感兴趣。
至于光速不变,我们上面已经分析了。只要坚持麦克斯韦方程组和相对性原理,光速不变就是一个自然而然的结论,并不是非要有实验才敢这样想。也就是说,有没有迈克尔逊-莫雷实验,爱因斯坦都能创立狭义相对论,我们不必过分夸大这个实验的作用。
所以,现在就是这样的局面,牌都在这里,你要怎么打?牛顿力学和麦克斯韦电磁学的核心冲突,牛顿和麦克斯韦这两尊大神之间的战争,你要怎么去化解?
我希望你能好好想一想,自己琢磨琢磨。谁都知道解决方案就是狭义相对论,但是只知道答案对你并没有太大的用处,我希望你自己能合乎逻辑地把正确答案推导出来。你也知道在试卷里只写一个答案但没有任何过程的后果吧?
这是科学史上难得一见场面,也是新手村的绝佳试炼基地。
以前的科学发展,大多是科学家在这个领域做了很多实验,总结了很多实验定律。最后再来个厉害人物对这些定律进行大综合,力学和电磁学的发展皆是如此。
但是,像狭义相对论这样,主要的发展动力来自两套在各自领域都工作良好,一结合就出矛盾的理论的情况是非常少见的。然而,我们现在又一次遇到了这种情况:广义相对论和量子力学在各自领域都工作良好,但是它们一结合就会出现无尽的灾难。
我们应该如何去协调广义相对论和量子力学呢?从这个角度来看,爱因斯坦成功协调牛顿力学和麦克斯韦电磁学的这次经验,是不是就更加显得弥足珍贵了呢?
我也很想知道,如果年轻的爱因斯坦在现在,他会如何看待广义相对论和量子力学之间的矛盾。科学家为了调和两者,提出的超弦理论、圈量子理论等有没有忽略什么关键性的东西?为什么引力没法量子化?我们对时空本性的认识,是不是又要发生一次大的变革?
这些问题有着无尽的吸引力,为了让我自己能尽早看到这些问题的答案,我现在竭尽全力给你们写科普。
所以,我不能只是简单地告诉你们答案,我得尽力把爱因斯坦的学习方式、思考方式、研究方式都写出来。让你们领会爱因斯坦的科学精神,然后让你们去思考这些大问题~
牛顿和麦克斯韦的战争就写到这里,至于爱因斯坦是如何化解这个矛盾的,我下一篇文章再细说。怕错过的,盯着我的公众号就行了。
当然,如果你能在这之前通过这篇文章的线索自己把问题解决了,自己独立地提出狭义相对论,那就再好不过了,那我简直要给你发一朵小红花。如果你有思路,但是在有的地方又卡壳了,可以来我的社群(后台回复“社群”)跟大家一起讨论,我相信这种方式对你的成长会大有裨益。
神探爱因斯坦,我们下篇文章见~
------------------------------------------
相关文章:
《最美的公式:你也能懂的麦克斯韦方程组(积分篇)》
《最美的公式:你也能懂的麦克斯韦方程组(微分篇)》
《见证奇迹的时刻:如何从麦克斯韦方程组推出电磁波?》
《闵氏几何是什么?它是如何统一时空并极大简化狭义相对论的?》
《你也能懂的微积分》
我是【长尾科技】,我正在尝试把专业的物理、数学内容用中小学生都能听懂的方式写出来,培养学生的科学思维,毕竟少年强则国强。喜欢就来关注我的公众号【长尾科技】~