详解生成对抗网络（GAN)

详解生成对抗网络（GAN)

本篇博文从以下几个结构介绍GAN模型

1. 概述

2. 模型优化训练

3. GAN的一些经典变种

   ---

   1 概述

GAN是由Ian Goodfellow于2014年首次提出，学习GAN的初衷，即生成不存在于真实世界的数据。类似于AI具有创造力和想象力。

GAN有两大护法G和D:

G是generator，生成器: 负责凭空捏造数据出来

D是discriminator，判别器: 负责判断数据是不是真数据

这样可以简单看作是两个网络的博弈过程。在原始的GAN论文里面，G和D都是两个多层感知机网络。GAN操作的数据不一定非是图像数据，在此用图像数据为例解释以下GAN：

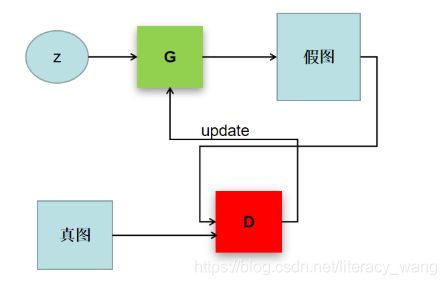
上图中，z是随机噪声（随机生成的一些数，也是GAN生成图像的源头）。D通过真图和假图的数据，进行一个二分类神经网络训练。G根据一串随机数就可以捏造出一个"假图像"出来，用这些假图去欺骗D，D负责辨别这是真图还是假图，会给出一个score。比如，G生成了一张图，在D这里评分很高，说明G生成能力是很成功的；若D给出的评分不高，可以有效区分真假图，则G的效果还不太好，需要调整参数。

---

2 模型优化训练

• ##### 通过图像解释：

GAN的训练过程，根据GAN的训练算法，如下图：

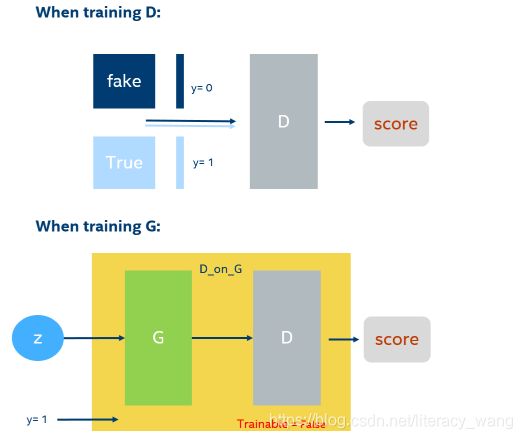
GAN的训练在同一轮梯度反转的过程中可以细分为2步：(1)先训练D；(2)再训练G。注意，不是等所有的D训练好了才开始训练G，因为D的训练也需要上一轮梯度反转中的G的输出值作为输入。

当训练D的时候：上一轮G产生的图片和真实图片，直接拼接在一起作为x。然后按顺序摆放成0和1，假图对应0，真图对应1。然后就可以通过D，x输入生成一个score（从0到1之间的数），通过score和y组成的损失函数，就可以进行梯度反传了。（我在图片上举的例子是batch = 1，len(y)=2*batch，训练时通常可以取较大的batch）

当训练G的时候：需要把G和D当作一个整体，这里取名叫做’D_on_G’。这个整体(简称DG系统)的输出仍然是score。输入一组随机向量z，就可以在G生成一张图，通过D对生成的这张图进行打分得到score，这就是DG系统的前向过程。score=1就是DG系统需要优化的目标，score和y=1之间的差异可以组成损失函数，然后可以采用反向传播梯度。注意，这里的D的参数是不可训练的。这样就能保证G的训练是符合D的打分标准的。这就好比：如果你参加考试，你别指望能改变老师的评分标准。

• ##### 通过公式解释

在训练过程中，生成网络的目标就是尽量生成真实的图片去欺骗判别网络D。而网络D的目标就是尽量把网络G生成的图片和真实的图片分别开来。这样，G和D构成了一个动态的“博弈过程”。这个博弈过程具体是怎么样的呢？

先了解下纳什均衡，纳什均衡是指博弈中这样的局面，对于每个参与者来说，只要其他人不改变策略，他就无法改善自己的状况。对应的，对于GAN，情况就是生成模型 G 恢复了训练数据的分布（造出了和真实数据一模一样的样本），判别模型再也判别不出来结果，准确率为 50%，约等于乱猜。这是双方网路都得到利益最大化，不再改变自己的策略，也就是不再更新自己的权重。

GAN模型的目标函数如下：

在这里，训练网络D使得最大概率地分对训练样本的标签（最大化log D(x)和log(1—D(G(z))))，训练网络G最小化log(1-D(G(z))），即最大化D的损失。而训练过程中固定一方，更新另一个网络的参数，交替迭代，使得对方的错误最大化，最终，G 能估测出样本数据的分布，也就是生成的样本更加的真实。

或者我们可以直接理解G网络的loss是log(1—D(G(z)))，

D的loss是 —(log D(x))+log(1—D(G(z))）

然后从式子中解释对抗，我们知道G网络的训练是希望D(G(z))趋近于1，也就是正类，这样G的loss就会最小。而D网络的训练就是一个2分类，目标是分清楚真实数据和生成数据，也就是希望真实数据的D输出趋近于1，而生成数据的输出即D(G(z))趋近于0，或是负类。这里就是体现了对抗的思想。

然后，这样对抗训练之后，效果可能有几个过程，原论文画出的图如下：

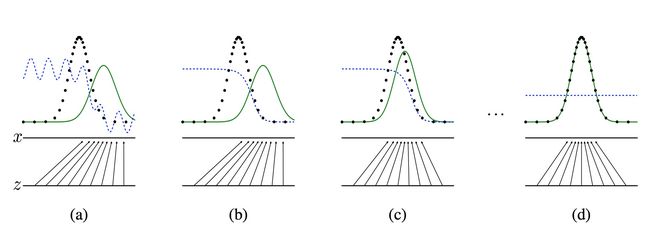
​ 黑色的线表示数据x的实际分布，绿色的线表示数据的生成分布，蓝色的线表示生成的数据对应在判别器中的分布效果

对于图a，D还刚开始训练，本身分类的能力还很有限，有波动，但是初步区分实际数据和生成数据还是可以的。图b，D训练得比较好了，可以很明显的区分出生成数据。然后对于图c：绿色的线与黑色的线的偏移，蓝色的线下降了，也就是生成数据的概率下降了。那么，由于绿色的线的目标是提升概率，因此就会往蓝色线高的方向移动。那么随着训练的持续，由于G网络的提升，G也反过来影响D的分布。假设固定G网络不动，训练D，那么训练到最优，

因此，随着p_g(x)趋近于p_data(x)，D_{g}^{*}会趋近于0.5，也就是到图d。而我们的目标就是希望绿色的线能够趋近于黑色的线，也就是让生成的数据分布与实际分布相同。

图d符合我们最终想要的训练结果。到这里，G网络和D网络就处于纳什均衡状态，无法再进一步更新了。

当然，这里说明只是图示，对于详细证明为什么最终会收敛到p_g(x)趋近于p_data(x)，就要看原论文了

然后看下原论文的整体算法：

简单理解：对于辨别器，如果得到的是生成图片辨别器应该输出 0，如果是真实的图片应该输出 1，得到误差梯度反向传播来更新参数。对于生成器，首先由生成器生成一张图片，然后输入给判别器判别并的到相应的误差梯度，然后反向传播这些图片梯度成为组成生成器的权重。直观上来说就是：辨别器不得不告诉生成器如何调整从而使它生成的图片变得更加真实。

---

3 GAN的一些经典变种

DCGAN:

DCGAN是继GAN之后比较好的改进，其主要的改进主要是在网络结构上，到目前为止，DCGAN的网络结构还是被广泛的使用，DCGAN极大的提升了GAN训练的稳定性以及生成结果质量。

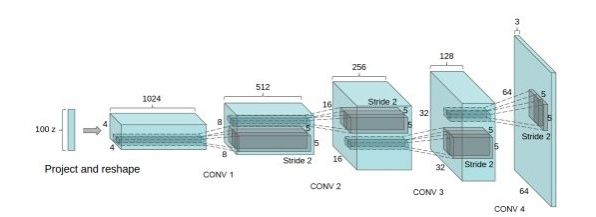
​ DCGAN中的G网络示意，相等于普通CNN的逆过程

DCGAN把上述的G和D用了两个卷积神经网络（CNN）。同时对卷积神经网络的结构做了一些改变，以提高样本的质量和收敛的速度，这些改变有：

• 取消所有pooling层。G网络中使用转置卷积（transposed convolutional layer）进行上采样，D网络中用加入stride的卷积代替pooling。

• 在D和G中均使用batch normalization

• 去掉FC层，使网络变为全卷积网络

• G网络中使用ReLU作为激活函数，最后一层使用tanh

• D网络中使用LeakyReLU作为激活函数

  DCGAN原文：Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks

WGAN和WGAN-GP

WGAN也是一篇经典，WGAN主要从损失函数的角度对GAN做了改进，损失函数改进之后的WGAN即使在全链接层上也能得到很好的表现结果，具体的来说，WGAN对GAN的改进有：

• 判别器最后一层去掉sigmoid

• 生成器和判别器的loss不取log

• 对更新后的权重强制截断到一定范围内，比如[-0.01，0.01]，以满足论文中提到的lipschitz连续性条件。

• 论文中也推荐使用SGD， RMSprop等优化器，不要基于使用动量的优化算法，比如adam。

  对于W-GAN的解释有很多，比如看穿机器学习(W-GAN模型)的黑箱。再比如令人拍案叫绝的Wasserstein GAN，有兴趣都可以看下，这篇论文实在经典。
  原文：[1701.07875] Wasserstein GAN

之前的WGAN虽然理论上有极大贡献，但在实验中却发现依然存在着训练困难、收敛速度慢的问题，这个时候WGAN-GP就出来了，它的贡献是：

• 提出了一种新的lipschitz连续性限制手法—梯度惩罚，解决了训练梯度消失梯度爆炸的问题。
• 比标准WGAN拥有更快的收敛速度，并能生成更高质量的样本
• 提供稳定的GAN训练方式，几乎不需要怎么调参，成功训练多种针对图片生成和语言模型的GAN架构

Conditional GAN

因为原始的GAN过于自由，训练会很容易失去方向，从而导致不稳定又效果差。而Conditional GAN就是在原来的GAN模型中加入一些先验条件，使得GAN变得更加的可控制。具体的来说，我们可以在生成模型G和判别模型D中同时加入条件约束y来引导数据的生成过程。条件可以是任何补充的信息，如类标签，其它模态的数据等。然后这样的做法应用也很多，比如图像标注，利用text生成图片等等。

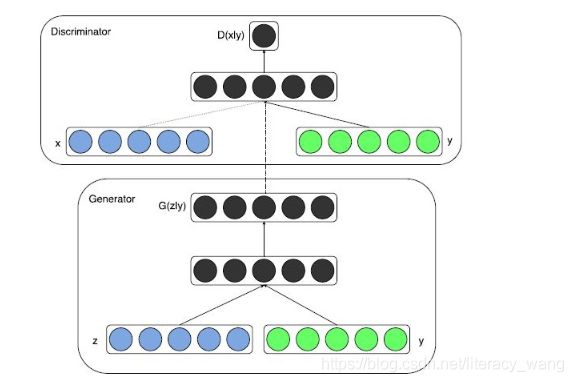
比之前的目标函数，Conditional GAN的目标函数其实差不多：

就是多了把噪声z和条件y作为输入同时送进生成器火热把数据x和条件y作为输入同时送进判别器（如上整体架构图）。这样在外加限制条件的情况下生成图片。