陆陆续续越来越多iOS开发者,进入到2020年求职跳槽高峰期. 2020年面试3大主流:iOS底层,算法数据结构, 音视频开发. 占了主要战场.
数据结构与算法面试,特别是图这一块成为了大多数iOS开发的败北一线大厂的主要原因. 今天给大家分享一个阿里的算法面试题.
题目(阿里面试算法真题):
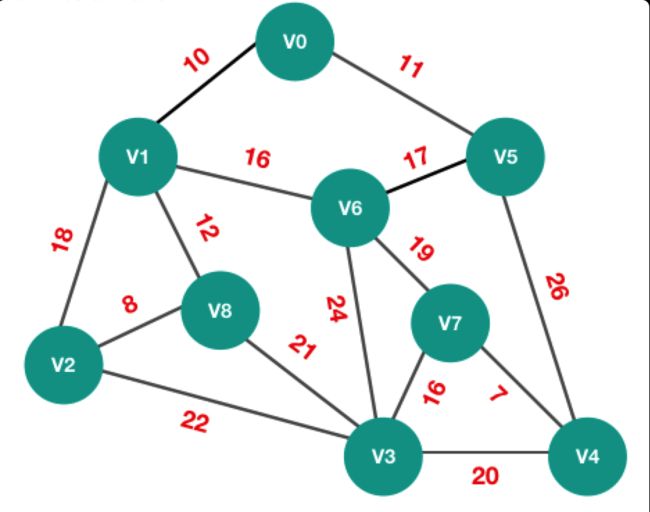
假设目前有N个顶点, 每个顶点连接的路径不一样,请设计一个算法,快速找到能覆盖所有顶点的路径;[可使用任何编程语言实现]
提示: 这个问题并不是求解图中2点间最短路径,而是设计一个路线,能够覆盖所有顶点的最优路径;
一. 题目解析
大多数开发者,拿到这个问题; 很容易想到求解图中2点间最短路径, 但其实并不是如此. 仔细阅读,会发现题目要求是设计一个路线能够覆盖所有的顶点; 这个用专业词汇,就是求解图中最小生成树;
最小生成树这个名词,出自数据结构. @如果对此不熟悉的,可以阅读 严蔚敏 所著《数据结构(C语言版)》
二. 解法
1:解法①
思路:
定义2个数组; adjvex 用来保存相关顶点下标; lowcost 保存顶点之间的权值
初始化2个数组, 从v0开始寻找最小生成树, 默认v0是最小生成树上第一个顶点
循环lowcost 数组,根据权值,找到顶点 k
更新lowcost 数组
循环所有顶点,找到与顶点k 有关系的顶点. 并更新lowcost 数组与adjvex 数组
动效图:
代码实现:
/* Prim算法生成最小生成树 */
void MiniSpanTree_Prim(MGraph G)
{
int min, i, j, k;
int sum = 0;
/* 保存相关顶点下标 */
int adjvex[MAXVEX];
/* 保存相关顶点间边的权值 */
int lowcost[MAXVEX];
/* 初始化第一个权值为0,即v0加入生成树 */
/* lowcost的值为0,在这里就是此下标的顶点已经加入生成树 */
lowcost[0] = 0;
/* 初始化第一个顶点下标为0 */
adjvex[0] = 0;
//1. 初始化
for(i = 1; i < G.numVertexes; i++) /* 循环除下标为0外的全部顶点 */
{
lowcost[i] = G.arc[0][i]; /* 将v0顶点与之有边的权值存入数组 */
adjvex[i] = 0; /* 初始化都为v0的下标 */
}
//2. 循环除了下标为0以外的全部顶点, 找到lowcost数组中最小的顶点k
for(i = 1; i < G.numVertexes; i++)
{
/* 初始化最小权值为∞, */
/* 通常设置为不可能的大数字如32767、65535等 */
min = INFINITYC;
j = 1;k = 0;
while(j < G.numVertexes) /* 循环全部顶点 */
{
/* 如果权值不为0且权值小于min */
if(lowcost[j]!=0 && lowcost[j] < min)
{
/* 则让当前权值成为最小值,更新min */
min = lowcost[j];
/* 将当前最小值的下标存入k */
k = j;
}
j++;
}
/* 打印当前顶点边中权值最小的边 */
printf("(V%d, V%d)=%d\n", adjvex[k], k ,G.arc[adjvex[k]][k]);
sum+=G.arc[adjvex[k]][k];
/* 3.将当前顶点的权值设置为0,表示此顶点已经完成任务 */
lowcost[k] = 0;
/* 循环所有顶点,找到与顶点k 相连接的顶点
1. 与顶点k 之间连接;
2. 该结点没有被加入到生成树;
3. 顶点k 与 顶点j 之间的权值 < 顶点j 与其他顶点的权值,则更新lowcost 数组;
*/
for(j = 1; j < G.numVertexes; j++)
{
/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j])
{
/* 将较小的权值存入lowcost相应位置 */
lowcost[j] = G.arc[k][j];
/* 将下标为k的顶点存入adjvex */
adjvex[j] = k;
}
}
}
printf("sum = %d\n",sum);
}
1:解法②
思路:
将邻接矩阵 转化成 边表数组;
对边表数组根据权值按照从小到大的顺序排序;
遍历所有的边, 通过 parent 数组找到边的连接信息; 避免闭环问题;
如果不存在闭环问题,则加入到最小生成树中. 并且修改 parent 数组
动效图:
代码实现:
/* 生成最小生成树 */
void MiniSpanTree_Kruskal(MGraph G)
{
int i, j, n, m;
int sum = 0;
int k = 0;
/* 定义一数组用来判断边与边是否形成环路
用来记录顶点间的连接关系. 通过它来防止最小生成树产生闭环;*/
int parent[MAXVEX];
/* 定义边集数组,edge的结构为begin,end,weight,均为整型 */
Edge edges[MAXEDGE];
/*1. 用来构建边集数组*/
for ( i = 0; i < G.numVertexes-1; i++)
{
for (j = i + 1; j < G.numVertexes; j++)
{
//如果当前路径权值 != ∞
if (G.arc[i][j]三. 总结
这个2个算法实现的出发点完全不一样; 第一种实现的策略是一边寻找一边标记; 而第二种思路则是先把所有的目标点进行排序.在进行查找标记;
推荐文集:
iOS面试题大全(上)
iOS面试题大全(下)
原文作者:才华美貌集于一身的CC
原文地址:HelloCode开发者学习平台