深度学习与围棋:为围棋数据设计神经网络
本文主要内容
- 构建一个深度学习应用,可以根据数据预测围棋的下一步动作。
- 介绍Keras深度学习框架。
- 了解卷积神经网络。
- 构建能够分析围棋空间数据的神经网络。
在第5章中,我们已经初步了解了神经网络的基本原理,并从零开始实现了一个前馈神经网络。在本章中,我们将把注意力转回围棋游戏,并解决如何使用深度学习技术来预测围棋游戏中任意给定棋局的下一步动作的问题。特别地,我们将使用第4章开发的树搜索技术来生成围棋游戏数据,然后用它们来训练神经网络。图6-1是我们将在本章中构建的应用的概览。
如图6-1所示,要利用好第5章中介绍的神经网络知识,必须先解决以下几个关键步骤。
图6-1 如何使用深度学习预测围棋游戏中的下一步动作
(1)在第3章中,我们专注于如何教计算机学会围棋规则,并在棋盘上实现对弈逻辑。第4章使用这些数据结构进行树搜索。在第5章中我们看到,神经网络需要的是数值输入,具体到我们所实现的前馈网络架构,它需要的是向量。
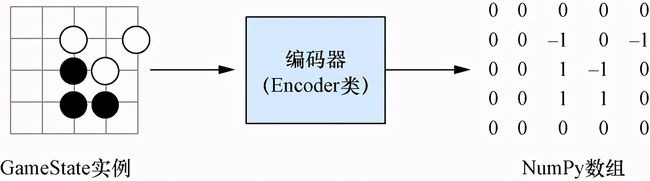
(2)为了能够输送到神经网络中,需要将围棋的棋局转换为输入向量。我们必须先创建一个编码器(encoder)来完成这个转换工作。图6-1绘制的是一个简单的编码器,我们将在6.1节中实现它。这个编码器可以将棋盘编码成相同尺寸的矩阵,其中白子表示为−1,黑子表示为1,空点表示为0。和前面章节中提到的MNIST数据类似,把这个矩阵展平就可以变换成一个向量。虽然这种表达方式过于简单,无法提供良好的动作预测结果,但它朝着正确方向迈出了第一步。第7章将介绍更复杂、更有效的棋盘编码方法。
(3)要训练神经网络来预测落子动作,首先必须准备好用于输入网络的数据。在6.2节中,我们将学习如何利用第4章中的技巧来生成棋谱。每一个讨论过的棋局都要进行编码,并转换为神经网络的训练特征,而棋盘的下一步动作,则作为训练标签使用。
(4)虽然像第5章那样自己实现神经网络很有用,但本章我们将引入更成熟的深度学习库以得到更快的速度和更高的可靠性。6.3节将介绍Keras,它是一个流行的Python深度学习库。我们将使用Keras建立神经网络模型,并预测落子动作。
(5)此时读者可能会觉得奇怪,为什么要把棋盘矩阵展平成向量,完全丢弃围棋棋盘的空间结构呢?在6.4节中,我们将了解一种称为卷积层(convolutional layer)的新网络层类型,它更适合围棋的应用场景。我们将使用卷积层来构建一种称为卷积神经网络(Convolutional Neural Network,CNN)的新网络架构。
(6)在本章的最后部分,我们将了解更多现代深度学习的关键概念,它们能帮助我们进一步提高预测落子动作的准确性。例如,6.5节会使用softmax更有效地预测概率;6.6节会用一种称为线性整流单元(Rectified Linear Unit,ReLU)的有趣函数作为激活函数,来构建更深层次的深度神经网络。
6.1 为神经网络编码围棋棋局
在第3章中我们构建了一个Python类库,它包含了围棋游戏中的所有实体:Player、Board、GameState等。现在我们想要把机器学习应用到围棋问题中,但神经网络这类数学模型无法像GameState类那样直接处理高级抽象对象,而只能处理向量或矩阵之类的数学对象。在本节中我们将创建一个Encoder类,它可以将围棋游戏对象转换为某种数学形式。之后,我们就能够把这种数学表示形式的数据输送给机器学习工具了。
要构建一个深度学习模型来预测围棋落子动作,第一步要加载能够输送给神经网络的数据。要实现这一点,可以给围棋棋盘定义一个简单的编码器,如图6-1所示。编码器是一种以适当的方式转换第3章中实现的围棋棋盘的方法。前面介绍过,多层感知机的输入形式是向量,而在6.4节中我们将看到另一种运行在更高维数据上的网络架构。图6-2展示了如何定义这类编码器的思路。
图6-2 编码器Encoder类的图示。它接收GameState类实例并将其转换为数学形式,即一个NumPy数组
编码器的核心在于如何编码完整的游戏状态。特别地,它应当定义如何编码棋盘上的单个点。有时候,与编码相反的过程也很有意思:如果已经用神经网络预测出下一手落子动作,而这个动作是已编码的,就需要把它转换回棋盘上的实际落子动作。这个反向操作称为解码,它是应用预测动作不可或缺的过程。
厘清了思路,现在就可以定义Encoder类了。这个类是本章和第7章里创建的各种编码器的通用接口。我们将在dlgo中定义一个名为encoders的新模块,以及一个空的__init__.py初始化文件,并在模块中放入文件base.py。然后,在这个文件中输入代码清单6-1所示的定义。
代码清单6-1 用于编码围棋游戏状态的抽象Encoder类
class Encoder:
def name(self): ⇽--- 让我们把模型正在使用的编码器名称输出到日志中或存储下来
raise NotImplementedError()
def encode(self, game_state): ⇽--- 将围棋棋盘转换为数值数据
raise NotImplementedError()
def encode_point(self, point): ⇽--- 将棋盘上的一个交叉点转换为一个整数索引
raise NotImplementedError()
def decode_point_index(self, index): ⇽--- 将整数索引转换回围棋棋盘上的交叉点
raise NotImplementedError()
def num_points(self): ⇽--- 棋盘上交叉点的总数,即棋盘宽度乘以棋盘高度
raise NotImplementedError()
def shape(self): ⇽--- 棋盘结构编码后的形状
raise NotImplementedError()编码器的定义很简单,但我们还想在base.py文件中添加一个便利功能:一个根据名称字符串来创建编码器的函数(如代码清单6-2所示)。这样就不需要显式地创建编码器对象了。把这个get_encoder_by_name函数附加在编码器定义的后面。
代码清单6-2 按名称创建围棋棋盘编码器
import importlib
def get_encoder_by_name(name, board_size): ⇽--- 可以根据编码器的名称来创建它的实例
if isinstance(board_size, int):
board_size = (board_size, board_size) ⇽--- 如果board_size是一个整数,则依据这个尺寸创建一个正方形棋盘
module = importlib.import_module('dlgo.encoders.' + name)
constructor = getattr(module, 'create') ⇽--- 每个编码器的实现类都必须提供一个“create”函数来创建新实例
return constructor(board_size)现在我们已经对编码器有了初步了解,也知道了如何创建编码器,接着就可以去实现图6-2中的想法,制作第一个编码器:黑白双方一方表示为1,另一方表示为−1,而空点表示为0。为了做出准确的预测,这个模型还需要知道下一回合的执子方。因此,我们用1来表示下一回合的执子方、−1表示其对手方,而不是固定用1表示黑方、−1表示白方。由于我们将围棋棋盘编码为与棋盘尺寸相同的单个矩阵(即一个特征平面),因此可以将这个编码器称为OnePlaneEncoder。在第7章中,我们还会看到具有多个特征平面(feature plane)的编码器,例如我们将实现一个具有3个平面的编码器,它用一个平面来表示黑方的棋盘布局,用另一个平面来表示白方的棋盘布局,还有一个平面表示劫争。本章我们暂时沿用简单的单平面思路,在oneplane.py文件中加以实现。代码清单6-3展示了实现的第一部分。
代码清单6-3 使用简单的单平面围棋棋盘编码器对游戏状态进行编码
import numpy as np
from dlgo.encoders.base import Encoder
from dlgo.goboard import Point
class OnePlaneEncoder(Encoder):
def __init__(self, board_size):
self.board_width, self.board_height = board_size
self.num_planes = 1
def name(self): ⇽--- 可以用名称“oneplane”来指代这个编码器
return 'oneplane'
def encode(self, game_state): ⇽--- 编码逻辑:对于棋盘上每一个交叉点,如果该点落下的是当前执子方的棋子,则在矩阵中填充1;如果是对手方的棋子,则填充−1;如果该点为空点,则填充0
board_matrix = np.zeros(self.shape())
next_player = game_state.next_player
for r in range(self.board_height):
for c in range(self.board_width):
p = Point(row=r + 1, col=c + 1)
go_string = game_state.board.get_go_string(p)
if go_string is None:
continue
if go_string.color == next_player:
board_matrix[0, r, c] = 1
else:
board_matrix[0, r, c] = -1
return board_matrix接着是定义的第二部分,将完成对棋盘上的单个交叉点进行编码和解码的工作。如代码清单6-4所示,编码过程将棋盘上的交叉点映射到尺寸为棋盘宽度乘以高度的向量,而解码过程则是从这个向量回溯棋盘交叉点坐标。
代码清单6-4 使用单平面围棋棋盘编码器对交叉点进行编码和解码
def encode_point(self, point): ⇽--- 将棋盘交叉点转换为整数索引
return self.board_width * (point.row - 1) + (point.col - 1)
def decode_point_index(self, index): ⇽--- 将整数索引转换为棋盘交叉点
row = index // self.board_width
col = index % self.board_width
return Point(row=row + 1, col=col + 1)
def num_points(self):
return self.board_width * self.board_height
def shape(self):
return self.num_planes, self.board_height, self.board_width关于围棋棋盘编码器的部分到此结束。接下来我们将生成能够编码并输送给神经网络的数据。
6.2 生成树搜索游戏用作网络训练数据
将机器学习应用于围棋比赛之前,我们需要准备一个训练数据集。幸运的是,各种公共围棋服务器上一直都有强大的棋手在进行对弈。我们会在第7章中介绍如何查找和处理这种棋谱并创建训练数据。现在我们可以先生成棋谱。本节介绍如何使用第4章创建的树搜索机器人来生成棋谱。在后面几节中,我们可以用这些机器人生成的棋谱作为训练数据来进行深度学习试验。
使用机器学习模仿经典算法看上去是不是有点傻?但如果传统算法非常慢,那就不一样了。在这里,对于速度慢的树搜索算法,我们希望用机器学习来迅速得到它的近似值。这一点正是AlphaGo Zero的关键概念。我们会在第14章介绍AlphaGo Zero的工作原理。
接下来,在dlgo模块之外创建一个名为generate_mcts_games.py的文件。从文件名就可以看出,这段代码的功能是用MCTS算法生成棋局。之后,我们会把每一局的每一回合都用6.1节中的OnePlaneEncoder进行编码,并存储在numpy数组中以备将来使用。我们需要先将代码清单6-5中的import语句放在这个文件的顶部。
代码清单6-5 用于生成蒙特卡洛树搜索棋局编码数据的模块的导入语句
import argparse
import numpy as np
from dlgo.encoders import get_encoder_by_name
from dlgo import goboard_fast as goboard
from dlgo import mcts
from dlgo.utils import print_board, print_move从这些导入语句中可以看到这个任务所需要的工具:mcts模块、第3章中的goboard实现以及6.1节刚定义的encoders模块。接下来编写生成游戏数据的函数generate_game,如代码清单6-6所示。在这个函数中,我们先用第4章的MCTSAgent实例来进行自我对弈(注意,可以利用第4章介绍的MCTS机器人的温度参数来调节树搜索的活跃度)。对于每一个动作,在落子之前对棋盘状态进行编码,然后将这个动作编码为一个独热向量,最后将它应用到棋盘上。
代码清单6-6 为本章生成MCTS棋局
def generate_game(board_size, rounds, max_moves, temperature):
boards, moves = [], [] ⇽--- 在boards变量中存储编码后的棋盘状态;而moves变量用于存放编码后的落子动作
encoder = get_encoder_by_name('oneplane', board_size) ⇽--- 用给定的棋盘尺寸、按名称初始化一个OnePlaneEncoder实例
game = goboard.GameState.new_game(board_size) ⇽--- 一个尺寸为board_size的新棋局被实例化好了
bot = mcts.MCTSAgent(rounds, temperature) ⇽--- 指定推演回合数与温度参数,创建一个蒙特卡洛树搜索代理作为我们的机器人
num_moves = 0
while not game.is_over():
print_board(game.board)
move = bot.select_move(game) ⇽--- 机器人选择下一步动作
if move.is_play:
boards.append(encoder.encode(game)) ⇽--- 把编码的棋盘状态添加到boards数组中
move_one_hot = np.zeros(encoder.num_points())
move_one_hot[encoder.encode_point(move.point)] = 1
moves.append(move_one_hot) ⇽--- 把下一步动作进行独热编码,并添加到moves数组中
print_move(game.next_player, move)
game = game.apply_move(move) ⇽--- 之后把机器人的下一步动作执行到棋盘上
num_moves += 1
if num_moves > max_moves: ⇽--- 继续下一步动作,直至达到最大动作数量限制
break
return np.array(boards), np.array(moves)现在我们就可以使用蒙特卡洛树搜索来创建和编码棋局数据了,接下来定义一个main方法来运行几盘棋,并保存它们,如代码清单6-7所示。这段代码也可以放在generate_mcts_games.py文件中。
代码清单6-7 为本章生成MCTS棋局的主函数
def main():
parser = argparse.ArgumentParser()
parser.add_argument('--board-size', '-b', type=int, default=9)
parser.add_argument('--rounds', '-r', type=int, default=1000)
parser.add_argument('--temperature', '-t', type=float, default=0.8)
parser.add_argument('--max-moves', '-m', type=int, default=60,
help='Max moves per game.')
parser.add_argument('--num-games', '-n', type=int, default=10)
parser.add_argument('--board-out')
parser.add_argument('--move-out')
args = parser.parse_args() ⇽--- 这个应用允许用命令行参数进行自定义设置
xs = []
ys = []
for i in range(args.num_games):
print('Generating game %d/%d...' % (i + 1, args.num_games))
x, y = generate_game(args.board_size, args.rounds, args.max_moves,
➥ args.temperature) ⇽--- 根据给定棋局数量来生成相应的棋局数据
xs.append(x)
ys.append(y)
x = np.concatenate(xs) ⇽--- 当所有棋局都生成之后,为棋局添加相应的特征与标签
y = np.concatenate(ys)
np.save(args.board_out, x) ⇽--- 根据命令行参数所指定的选项,将特征与标签数据存放到不同的文件中
np.save(args.move_out, y)
if __name__ == '__main__':
main()有了这个实用工具程序,我们就可以轻松地生成棋局数据了。例如,假设我们想生成20局9×9围棋的棋局数据,并将特征存放在features.npy文件中,将标签存放在labels.npy文件中,那么可以执行下面的命令:
python generate_mcts_games.py -n 20 --board-out features.npy
➥ --move-out labels.npy注意,生成这样的棋局数据可能会相当缓慢,因此需要等待一段时间才能够生成大量的游戏。我们可以选择减少MCTS的轮数,但这也会相应降低机器人的棋力段位。因此,我们已经事先生成了一些棋局数据,可以在本书GitHub代码库中的generated_games目录中找到。对应的棋局输出文件为features-40k.npy和labels-40k.npy。这些数据包含了大约40 000个回合,相当于几百局棋。这些棋局数据在生成时设置为每回合进行5 000轮MCTS。在这种条件下,MCTS引擎大多数情况下都能够合理发挥,因此我们也可以期望神经网络能够学会如何模仿它。
至此我们已经完成了预处理的全部工作,下一步就可以将神经网络应用于生成的数据了。我们可以直接用第5章中的网络实现来做到这一点,而这么做也不失为一个很好的练习。但展望未来,我们需要一个更强大的工具来满足日益复杂的深度神经网络需求。下一节将介绍Keras深度学习库。
6.3 使用Keras深度学习库
随着许多强大的、封装了底层抽象的深度学习库的出现,神经网络的梯度和反向传递的计算正渐渐变为失传的技艺。在第5章中,我们从零开始实现了一个神经网络,这么做益处颇多,现在是时候转向结构更成熟、特性更丰富的软件了。
Keras深度学习库是一个用Python编写的结构优雅、广泛流行的深度学习工具。这个开源项目创建于2015年,并迅速积累了巨大的用户群。它的代码托管在GitHub上,并在官方网站上提供了优秀的文档。
6.3.1 了解Keras的设计原理
Keras的主要优势之一,就是它的API非常直观,因此很容易上手,并能帮助开发者实现快速原型设计和快速实验周期。这使Keras成为许多数据科学竞赛的热门选择。Keras吸收了其他深度学习工具(如Torch)的理念,并采用了模块化的构建块形式。它的另一大优势是可扩展性,让我们可以很直观地添加新的自定义层,或者扩展现有功能。
还有一个原因让Keras很容易上手,那就是它的功能非常齐全。例如,很多流行的类似MNIST数据集都可在Keras中直接加载,并且在GitHub代码库中还可以找到很多优秀的示例。最重要的是,GitHub上记录了Keras的完整生态体系,包括各种Keras扩展和独立项目,并由开源社区建设维护。
此外,Keras还有一个与众不同的“后端”概念:这个库可以用几个不同的强大引擎来运行,而且可以根据需求切换后端引擎。我们可以把Keras看作是深度学习体系的“前端”:它提供一系列方便的高级抽象和功能库来运行算法模型,而后台繁重的工作则可以选择一个后端服务来负责运行。截至编写本书时,Keras的官方后端有3个:TensorFlow、Theano和Microsoft Cognitive Toolkit。在本书中我们将使用谷歌的TensorFlow库作为默认后端,它同时也是Keras的默认后端。如果读者对其他后端有所偏好,由于Keras处理好了大部分的差异细节,切换起来也不费劲。
在本节中,我们将先学习如何安装Keras,然后通过运行第5章中的手写数字识别示例代码来了解其API,最后继续完成围棋落子动作预测的任务。
6.3.2 安装Keras深度学习库
要开始使用Keras,需要先安装一个后端服务。我们可以先选用TensorFlow。安装它最便捷的途径是用pip命令,如下所示:
pip install tensorflow如果你的计算机配有NVIDIA GPU,并安装了最新的CUDA驱动程序,那么可以尝试安装GPU加速版TensorFlow:
pip install tensorflow-gpu如果tensorflow-gpu与你的硬件和驱动程序相互兼容,就会有巨大的速度提升。
Keras还有几个可选的依赖库,如有助于模型序列化与可视化的组件。不过我们暂时先跳过它们,直接继续安装Keras深度学习库本身:
pip install Keras6.3.3 热身运动:在Keras中运行一个熟悉的示例
本节中我们将看到用来定义和运行Keras模型所需要遵循的4步工作流程。
(1)数据预处理——加载并准备将要输送到神经网络的数据集。
(2)模型定义——将模型实例化,并根据需要向其添加具体层。
(3)模型编译——使用优化器、损失函数以及一系列评估指标(可选)来编译先前定义的模型。
(4)模型训练与评估——在数据上训练深度学习模型,并进行评估。
为了尽快上手Keras,我们将引导你完成第5章中所展示的用例:使用MNIST数据集来预测手写数字。后面我们将看到,第5章中的简单模型定义已经和Keras语法相当接近了,因此换用Keras应该更加轻松。
在Keras中可以定义两种类型的模型:顺序模型和更通用的非顺序模型。本章中我们仅使用顺序模型。两种模型的类定义都可以在keras.models中找到。要定义顺序模型,必须向它添加具体的层,这一点和第5章的实现一样。Keras层可在keras.layers模块获得。用Keras加载MNIST数据集也很简单,这个数据集可以在keras.datasets模块中找到。开始定义这个应用解决方案之前,我们先导入它的全部依赖,如代码清单6-8所示。
代码清单6-8 从Keras导入模型、层和数据集
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense下一步是加载并预处理MNIST数据。在Keras中,这个步骤只需几行代码即可实现。加载完成之后,将60 000个训练样本和10 000个测试样本数据展平,再转换为float类型,然后除以255,将输入数据进行归一化处理。这样做是由于数据集中的像素值变化范围是0~255,因此把它们归一化为[0, 1]的范围之后可以使神经网络的训练更方便。此外,和第5章中一样,标签必须采用独热编码。代码清单6-9展示了如何用Keras执行上述操作。
代码清单6-9 使用Keras加载和预处理MNIST数据
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)数据准备好之后,现在可以继续定义神经网络了。在Keras中初始化一个Sequential模型,然后逐个添加多个层,如代码清单6-10所示。为第一层提供参数input_shape来指明输入数据的形状。在我们的例子里,输入数据是一个维度为784的向量,因此应当提供参数input_shape = (784,)。Keras中的Dense层在创建时可以提供关键字参数activation,以指定这个稠密层的激活函数。我们选择sigmoid激活函数,这也是目前唯一介绍过的激活函数。Keras里还有很多激活函数,我们会在后续章节中深入讨论。
代码清单6-10 用Keras构建一个简单的顺序模型
model = Sequential()
model.add(Dense(392, activation='sigmoid', input_shape=(784,)))
model.add(Dense(196, activation='sigmoid'))
model.add(Dense(10, activation='sigmoid'))
model.summary()创建Keras模型的下一步是用一个损失函数和优化器来编译(compile)模型,如代码清单6-11所示。可以用名称字符串来指定这两个参数:损失函数选择mean_squared_error(均方误差),优化器则选择sgd(随机梯度下降)。同样地,Keras还有很多损失函数和优化器可供选择,但作为上手示例,我们可以先用第5章中已经介绍过的这两个即可。另外,Keras模型的编译步骤中还可额外提供一个参数metrics来指定多个评估指标。对我们的第一个应用来说,使用accuracy(准确率)这一个指标就够了。accuracy指标用来度量模型得分最高的预测输出与数据的真实标签之间匹配的频率。
代码清单6-11 编译Keras深度学习模型
model.compile(loss='mean_squared_error',
optimizer='sgd',
metrics=['accuracy'])最后一步是执行网络的训练步骤,然后用测试数据对它进行评估,如代码清单6-12所示。我们可以在model上调用fit函数来完成这一步。调用时指定的参数包括训练数据集、小批量尺寸以及运行的迭代周期数。
代码清单6-12 训练和评估Keras模型
model.fit(x_train, y_train,
batch_size=128,
epochs=20)
score = model.evaluate(x_test, y_test)
print('Test loss:', score[0])
print('Test accuracy:', score[1])总结一下,构建和运行Keras模型分为4个步骤:数据预处理、模型定义、模型编译以及模型训练与评估。Keras的核心优势之一是可以快速完成这个4步循环,从而实现快速实验周期。这一点非常重要。因为通常情况下,初始的模型定义仅通过调整参数就可以得到很大的改进。
6.3.4 使用Keras中的前馈神经网络进行动作预测
现在读者应当已经对Keras顺序神经网络的API有所了解,让我们回到围棋动作预测的应用场景。图6-3展示了训练过程中的这个步骤。首先需要加载6.2节生成的围棋棋谱数据,如代码清单6-13所示。注意与之前的MNIST数据一样,围棋棋盘数据需要展平为向量。
图6-3 神经网络可以用来预测围棋落子动作。如果已经将游戏状态编码为矩阵,就可以把这个输送给动作预测模型了。模型的输出是一个代表各个可能动作概率的向量
代码清单6-13 加载并预处理先前存储的围棋棋谱数据
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
np.random.seed(123) ⇽--- 设置一个固定的随机种子,以确保这个脚本可以严格重现
X = np.load('../generated_games/features-40k.npy') ⇽--- 将样本数据加载到NumPy数组中
Y = np.load('../generated_games/labels-40k.npy')
samples = X.shape[0]
board_size = 9 * 9
X = X.reshape(samples, board_size) ⇽--- 将输入数据由9×9的矩阵转换为维度为81的向量
Y = Y.reshape(samples, board_size)
train_samples = int(0.9 * samples) ⇽--- 预留数据集的10%作为测试集;其他的90%用于训练
X_train, X_test = X[:train_samples], X[train_samples:]
Y_train, Y_test = Y[:train_samples], Y[train_samples:]接下来我们用上面定义的特征X和标签Y来定义一个用于预测围棋动作的模型,并运行它。9×9棋盘有81种可能的落子动作,因此网络需要预测81个分类。我们先讨论一下最简单的情形,假设我们闭上眼睛,随意指出棋盘上的一个位置,这样就有1/81的机会纯粹依靠运气就能选对下一回合动作,即准确率为1.2%。因此,我们希望做出来的模型的准确率能够显著超过1.2%。
定义一个简单Keras多层感知机,包含3个Dense(稠密层),激活函数均为sigmoid,并采用均方误差作为损失函数、随机梯度下降作为优化器进行编译。之后用这个网络进行15个迭代周期的训练,并使用测试数据进行评估,如代码清单6-14所示。
代码清单6-14 在生成的围棋棋谱数据上运行Keras多层感知机
model = Sequential()
model.add(Dense(1000, activation='sigmoid', input_shape=(board_size,)))
model.add(Dense(500, activation='sigmoid'))
model.add(Dense(board_size, activation='sigmoid'))
model.summary()
model.compile(loss='mean_squared_error',
optimizer='sgd',
metrics=['accuracy'])
model.fit(X_train, Y_train,
batch_size=64,
epochs=15,
verbose=1,
validation_data=(X_test, Y_test))
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])执行这段代码,可以在控制台看到输出的模型摘要和评估指标:
__________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 1000) 82000
__________________________________________________
dense_2 (Dense) (None, 500) 500500
__________________________________________________
dense_3 (Dense) (None, 81) 40581
=================================================================
Total params: 623,081
Trainable params: 623,081
Non-trainable params: 0
__________________________________________________
...
Test loss: 0.0129547887068
Test accuracy: 0.0236486486486注意输出中的Tranable params: 623,081这一行,它表示训练过程中维护了超过60万个独立权重。这是模型计算强度的一个粗略的指标,它还可以粗略地估计模型的容量(capacity),即它学习复杂关系的能力。当比较不同的网络架构时,参数总数可以用来近似地比较模型的体量。
从输出可以看到,实验的预测准确率仅为 2.3%左右,这并不能令人满意。但请注意,前面讲的随机猜测动作的基础实现,准确率是 1.2%。也就是说,尽管模型表现得不是很好,但它确实学到了一些东西,预测动作的效果比随机猜测好。
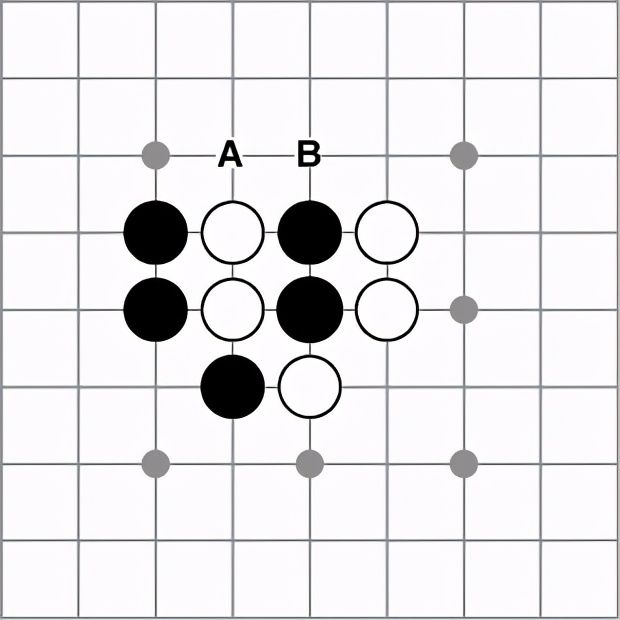
我们可以向模型输入特定的棋局来查看它的大致情况。图6-4展示了我们设计的一个棋局状态,它的正确落子动作显而易见。下一回合执子方可以在A点或B点落子来吃掉对方两颗子。另外,这个棋局并不在我们的训练集中。
图6-4 用于测试模型的示例棋局。在这个棋局中,黑方可以通过在A点落子来吃掉白方两颗子,而白方也可以在B点落子来吃掉黑方两颗子。在这里,先落子的一方会占握巨大的优势
现在,可以将这个棋局输入训练模型中,并输出它的预测结果,如代码清单6-15所示。
代码清单6-15 用已知的棋局来评估模型
test_board = np.array([[
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, -1, 1, -1, 0, 0, 0, 0,
0, 1, -1, 1, -1, 0, 0, 0, 0,
0, 0, 1, -1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0,
]])
move_probs = model.predict(test_board)[0]
i = 0
for row in range(9):
row_formatted = []
for col in range(9):
row_formatted.append('{:.3f}'.format(move_probs[i]))
i += 1
print(' '.join(row_formatted))输出如下所示:
0.037 0.037 0.038 0.037 0.040 0.038 0.039 0.038 0.036
0.036 0.040 0.040 0.043 0.043 0.041 0.042 0.039 0.037
0.039 0.042 0.034 0.046 0.042 0.044 0.039 0.041 0.038
0.039 0.041 0.044 0.046 0.046 0.044 0.042 0.041 0.038
0.042 0.044 0.047 0.041 0.045 0.042 0.045 0.042 0.040
0.038 0.042 0.045 0.045 0.045 0.042 0.045 0.041 0.039
0.036 0.040 0.037 0.045 0.042 0.045 0.037 0.040 0.037
0.039 0.040 0.041 0.041 0.043 0.043 0.041 0.038 0.037
0.036 0.037 0.038 0.037 0.040 0.039 0.037 0.039 0.037这个矩阵与9×9的棋盘一一映射:每个数字代表模型在棋盘这个点上下一回合落子的置信度。模型输出的结果并不太好:它甚至连不能在被棋子占据的地方落子都没有学会。但请注意,棋盘边缘的得分始终低于靠近中心的得分。而根据围棋传统,除终盘或者其他特殊情况之外,应该尽量避免在棋盘边缘落子。这样看来,我们的模型已经学会了一个围棋相关的合理概念。它并没有依靠对围棋策略或者落子效率的理解,而是简单地模仿我们的MCTS机器人所做的事情。这个模型也许不能预测很多强力的落子动作,但它至少已经学会了避免一整类非常糟糕的动作。
这已经可以算是真正的进步了,但我们还可以做得更好。第一次实验中所展现出来的几个问题,将在本章后面几节分别得到处理,围棋落子动作的预测准确率也会逐渐提高。我们需要解决下面几个问题。
- 这个预测模型使用的数据是由树搜索算法生成的,而这个算法的随机性很高。有时候MCTS引擎会产生很奇怪的动作,尤其在遥遥领先或远远落后的局面下。在第7章中我们将利用人工棋谱数据创建一个深度学习模型。当然,人类的策略也有出乎意料的时候,但他们至少不会下一些毫无道理的废棋。
- 本章使用的神经网络架构还有很大的改进空间。在多层感知机中,因为必须将二维的棋盘数据展平为一维向量,从而丢失了棋盘相关的全部空间信息,所以它其实并不太适合用来处理围棋棋盘数据。6.4节将介绍一种新型的神经网络,它可以更好地捕获围棋棋盘的结构。
- 到目前为止,在所有网络中我们都只用过sigmoid这一个激活函数。6.5节和6.6节将介绍两种新的激活函数,它们通常可以产生更好的结果。
- 到目前为止,我们只用过MSE这一个损失函数。它很直观,但并不太适合我们的使用场景。6.5节我们将采用为分类任务量身定制的损失函数。
在本章的结尾,上述问题大多得到解决之后,我们就能够构建出一个比首次尝试更加优秀的模型,能够更好地预测动作。在第7章中我们还会学习构建更加强大的机器人的关键技术。
注意,我们的最终目标不是尽量准确地预测落子动作,而是要创建一个更强的围棋机器人。因此,虽然深层神经网络永远也无法在历史棋局的下一步动作预测上做得更好,但深度学习的强大之处在于它们仍然能隐式地捕获棋局的结构,并找到合理的甚至非常优秀的落子动作。
本文截选自《深度学习与围棋》
1.本书是一本人工智能的实践性入门教程,成功地把AlphaGo这个人工智能领域中最激动人心的里程碑之一,转化为一门优秀的入门课程;
2.采用Keras深度学习框架,用Python来实现代码;
3.内容全面,层次划分细致,基本上将AlphaGo背后所有的理论知识都覆盖了;
4.提供配套源代码。
围棋这个古老的策略游戏是AI研究的特别适用的案例。2016年,一个基于深度学习的系统战胜了围棋世界冠军,震惊了整个围棋界。不久之后,这个系统的升级版AlphaGo Zero利用深度强化学习掌握了围棋技艺,轻松击败了其原始版本。读者可以通过阅读本书来学习潜藏在它们背后的深度学习技术,并构建属于自己的围棋机器人!
本书通过教读者构建一个围棋机器人来介绍深度学习技术。随着阅读的深入,读者可以通过Python深度学习库Keras采用更复杂的训练方法和策略。读者可以欣赏自己的机器人掌握围棋技艺,并找出将学到的深度学习技术应用到其他广泛的场景中的方法。