2021年 第12届 蓝桥杯 第3次模拟赛真题详解及小结【Java版】

• 蓝桥杯 Java B组 省赛决赛 真题详解及小结汇总【2013年(第4届)~2021年(第12届)】
• 第11届 蓝桥杯-第1、2次模拟(软件类)真题-(2020年3月、4月)-官方讲解视频

---

• 说明：大部分题解思路及程序代码 源自 蓝桥杯 官网视频(Java B组历年真题解析) —— 郑未老师。

1. 2013年 第04届 蓝桥杯 Java B组 省赛真题详解及小结
2. 2014年 第05届 蓝桥杯 Java B组 省赛真题详解及小结
3. 2015年 第06届 蓝桥杯 Java B组 省赛真题详解及小结
4. 2016年 第07届 蓝桥杯 Java B组 省赛真题详解及小结
5. 2017年 第08届 蓝桥杯 Java B组 省赛真题详解及小结
6. 2018年 第09届 蓝桥杯 Java B组 省赛真题详解及小结
7. 2019年 第10届 蓝桥杯 Java B组 省赛真题详解及小结
8. 2020年 第11届 蓝桥杯 第1次模拟赛真题详解及小结【Java版】（校内模拟）// 官方讲解视频
9. 2020年 第11届 蓝桥杯 第2次模拟赛真题详解及小结【Java版】// 官方讲解视频
10. 2020年 第11届 蓝桥杯 C/C++ B组 省赛真题详解及小结【第1场省赛 2020.07.05】【Java版】
11. 2020年 第11届 蓝桥杯 Java B组 省赛真题详解及小结【第1场省赛 2020.07.05】
12. 2020年 第11届 蓝桥杯 Java C组 省赛真题详解及小结【第1场省赛 2020.07.05】
13. 2020年 第11届 蓝桥杯 Java B组 省赛真题详解及小结【第2场省赛 2020.10.17】
14. 2021年 第12届 蓝桥杯 第1次模拟赛真题详解及小结【Java版】
15. 2021年 第12届 蓝桥杯 第2次模拟赛真题详解及小结【Java版】
16. 2021年 第12届 蓝桥杯 第3次模拟赛真题详解及小结【Java版】
17. 2021年 第12届 蓝桥杯 第4次模拟赛真题详解及小结【Java版】
18. 2021年 第12届 蓝桥杯【备赛 直播 公开课 —— 软件类（本科组、高职高专组）】
19. 2021年 第12届 蓝桥杯 Java B组 省赛真题详解及小结【第1场省赛 2021.04.18】
20. 2021年 第12届 蓝桥杯 Java B组 省赛真题详解及小结【第2场省赛 2021.05.09】

---

1. 2015年 第06届 蓝桥杯 Java B组 决赛真题详解及小结
2. 2016年 第07届 蓝桥杯 Java B组 决赛真题详解及小结
3. 2017年 第08届 蓝桥杯 Java B组 决赛真题详解及小结
4. 2018年 第09届 蓝桥杯 Java B组 决赛真题详解及小结
5. 2019年 第10届 蓝桥杯 Java B组 决赛真题详解及小结
6. 2020年 第11届 蓝桥杯 Java B组 决赛真题详解及小结【2020.11.14】
7. 2021年 第12届 蓝桥杯 Java B组 决赛真题详解及小结

目录

模拟赛网页截图

一、试题A——答案：800

解法一：循环+gcd()

二、试题B——答案：81

解法一

三、试题C——答案：12

解法一

解法二

四、试题D——答案：1001

解法一：概念计算

解法二

五、试题E——答案：BYS

解法一：手工计算

解法二

解法三：Excel列计算（通用版）

六、试题F

解法一

七、试题G

解法一【错误解法】

解法二

八、试题H

解法一

九、试题I

解法一

九、试题I（2）

解法一

十、试题J

解法一

小结

---

仅供参考，欢迎指正！以下均为个人想法和解题思路，如有错误或不足，欢迎指正。

模拟赛网页截图

 

一、试题A——答案：800

问题描述

　　请问在 1 到 2020 中，有多少个数与 2020 互质，即有多少个数与 2020 的最大公约数为 1。

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

解法一：循环+gcd()

【答案】：800

package simulationMatch_12_2021_3;

public class _01A {
	public static void main(String[] args) {
		int answer = 0;
		for (int i = 1; i <= 2020; i++) {
			if (gcd(2020, i) == 1) { // 若两数最大公约数是1，则answer++
				answer++;
				System.out.print(i + "、");
			}
		}
		System.out.println("\n" + answer);
	}

	/**
	 * 返回最大公约数
	 * 
	 * @param a
	 * @param b
	 * @return
	 */
	public static int gcd(int a, int b) {
		return b == 0 ? a : gcd(b, a % b);
	}
}

二、试题B——答案：81

问题描述

　　ASCII 码将每个字符对应到一个数值（编码），用于信息的表示和传输。在 ASCII 码中，英文字母是按从小到大的顺序依次编码的，例如：字母 A 编码是 65, 字母 B 编码是 66，字母 C 编码是 67，请问字母 Q 编码是多少？

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

解法一

【答案】：81

package simulationMatch_12_2021_3;

public class _02B {
	public static void main(String[] args) {
		System.out.println('A' - 0); // 65
		System.out.println('B' - 0); // 66
		System.out.println('C' - 0); // 67
		System.out.println('Q' - 0); // 81
		System.out.println('Q' + 0); // 81
		System.out.println('Z' - 0); // 90
	}
}

三、试题C——答案：12

问题描述

　　对于整数 v 和 p，定义 Pierce 序列为：
　　a[1] = v
　　a[i] = p % a[i-1]
　　例如，当 v = 8, p = 21 时，对应的 Pierce 序列为
　　a[1] = 8
　　a[2] = 5
　　a[3] = 1
　　再往后计算，值变为 0，不在我们考虑的范围内。因此当 v = 8, p = 21 时， Pierce 序列的长度为 3。
　　当 p 一定时，对于不同的 v 值，Pierce 序列的长度可能不同。当 p = 8 时，若 1<=v 　　当 p=2021 时，最长的 Pierce 序列出现在 v=1160 时，请问这个序列有多长？

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

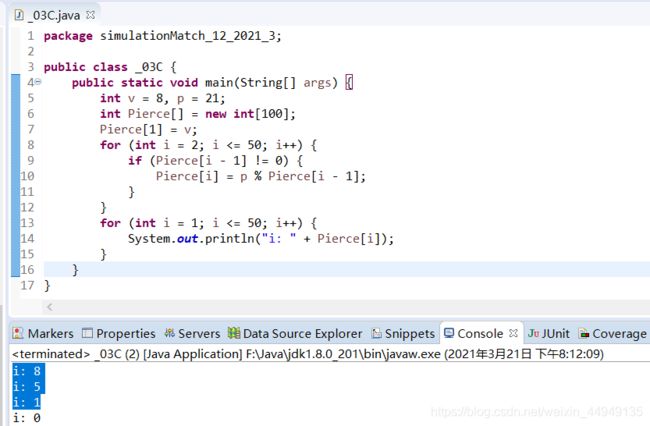
解法一

【答案】：12

package simulationMatch_12_2021_3;

public class _03C {
	public static void main(String[] args) {
		function(8, 21);
		System.out.println("--------------");
		function(13, 8);
		System.out.println("--------------");
		function(1160, 2021);
	}

	public static void function(int v, int p) {
		// int v = 8, p = 21;
		// int v = 13, p = 8;
		// int v = 1160, p = 2021;
		int Pierce[] = new int[100];
		Pierce[1] = v;
		for (int i = 2; i <= 50; i++) {
			if (Pierce[i - 1] != 0) {
				Pierce[i] = p % Pierce[i - 1];
			}
		}
		for (int i = 1; i <= 50; i++) {
			if (Pierce[i] != 0) {
				System.out.println(i + ": " + Pierce[i]);
			}
		}
	}
}

解法二

原文链接：1.0219——2021年第十二届蓝桥杯第三场校模拟赛

package simulationMatch_12_2021_3;

public class _03C2 {
	public static void main(String[] args) {
		int v = 1160, p = 2021, ans = 1;
		while (p % v != 0) {
			v = p % v;
			++ans;
		}
		System.out.println(ans);
	}
}

四、试题D——答案：1001

问题描述

　　有一棵二叉树，一个由2021个结点，其中有1000个结点有两个子结点，其他的结点有一个或者0个子结点。
　　请问，这棵二叉树有多少个叶结点？

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

解法一：概念计算

【答案】：1001

• 非空二叉树上的叶子结点数（度为0的节点，称为“叶子结点”）等于度为2的结点数加1，即  。
• 设度为0、1、2的结点个数分别为、、，二叉树的节点总数  。

n = n2 + n1 + n0 = 2021，n2 = 1000，n0 = n2 + 1 = 1000 + 1 = 1001 。

解法二

【答案】：1001

package simulationMatch_12_2021_3;

public class _04D {
	public static void main(String[] args) {
		System.out.println((int) (Math.pow(2, 10 - 1) - 23) * 2 + 23);
	}
}

五、试题E——答案：BYS

问题描述

　　在 Excel 中，第 1 列到第 26 列的列名依次为 A 到 Z，从第 27 列开始，列名有两个字母组成，第 27 列到第 702 列的列名依次为 AA 到 ZZ。
　　之后的列再用 3 个字母、4 个字母表示。
　　请问，第 2021 列的列名是什么？

答案提交

　　这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个有大写字母组成的字符串，在提交答案时只填写这个字符串，填写多余的内容将无法得分。

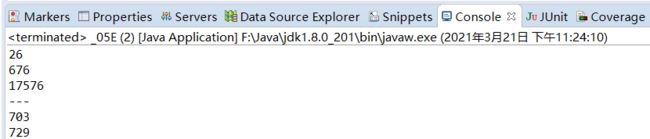
解法一：手工计算

【答案】：BYS

package simulationMatch_12_2021_3;

public class _05E {
	public static void main(String[] args) {
		System.out.println(26); // 26【A-Z】
		System.out.println(26 * 26); // 676【AA-ZZ】676+26=702
		System.out.println(26 * 26 * 26); // 17576【AAA-ZZZ】
		System.out.println("---");
		for (int i = 703; i <= 2021; i += 26) {
			System.out.println(i);
		}
	}
}

解法二

原文链接：1.0219——2021年第十二届蓝桥杯第三场校模拟赛

package simulationMatch_12_2021_3;

public class _05E2 {

	public static void main(String[] args) {
		int n = 2021;
		StringBuilder stb = new StringBuilder("");
		while (n != 0) {
			stb.append((char) (((n - 1) % 26) + 'A'));
			n = (n - 1) / 26;
		}
		System.out.println(stb.reverse().toString()); // BYS
	}

}

解法三：Excel列计算（通用版）

原文链接：LuckyCCat——【蓝桥杯2017Java】Excel地址

package simulationMatch_12_2021_3;

import java.util.Scanner;

public class _05E3 {
	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int target = input.nextInt();
		char[] ans = new char[1000000];
		int index = 0;
		while (target > 0) {
			int temp = target % 26;
			if (temp == 0) { // 特殊情况，能除尽的情况下，26作为余数
				ans[index++] = 'Z';
				target = target / 26 - 1;
			} else { // 不需要进位
				ans[index++] = (char) ('A' + temp - 1); // 记录余数
				target = target / 26; // 把商作为新的被除数
			}
		}
		for (int i = index - 1; i >= 0; i--) {
			System.out.print(ans[i]);
		}
	}
}

六、试题F

问题描述

　　在书写一个较大的整数时，为了方便看清数位，通常会在数位之间加上逗号来分割数位，具体的，从右向左，每三位分成一段，相邻的段之间加一个逗号。
　　例如，1234567 写成 1,234,567。
　　例如，17179869184 写成 17,179,869,184。
　　给定一个整数，请将这个整数增加分割符后输出。

输入格式

　　输入一行包含一个整数 v。

输出格式

　　输出增加分割符后的整数。

样例输入

1234567

样例输出

1,234,567

样例输入

17179869184

样例输出

17,179,869,184

数据规模和约定

　　对于 50% 的评测用例，0 <= v < 10^9 (10的9次方)。
　　对于所有评测用例，0 <= v < 10^18 (10的18次方)。

解法一

原文链接：1.0219——2021年第十二届蓝桥杯第三场校模拟赛

package simulationMatch_12_2021_3;

import java.util.Scanner;

public class _06F {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		long v = sc.nextLong();
		char[] ch = new String(v + "").toCharArray();
		if (ch.length <= 3) {
			System.out.println(v);
		} else if (ch.length % 3 == 0) {
			System.out.print("" + ch[0] + ch[1] + ch[2]);
			for (int i = 3; i < ch.length; i += 3)
				System.out.print("," + ch[i] + ch[i + 1] + ch[i + 2]);
		} else {
			for (int i = 0; i < ch.length % 3; ++i)
				System.out.print(ch[i]);
			for (int i = ch.length % 3; i < ch.length; i += 3)
				System.out.print("," + ch[i] + ch[i + 1] + ch[i + 2]);
		}
	}
}

七、试题G

问题描述

　　斐波那契数列是这样一个数列：它的第一项和第二项都是1，从第三项开始每一项都是前两项的和。
　　根据以上定义，我们容易计算出斐波那契数列的前几项依次是：1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ……
　　现在请你计算斐波那契数列第N项是奇数还是偶数？

输入格式

　　输入的包含一个整数N。

输出格式

　　如果是奇数输出1，是偶数输出0。

样例输入

10

样例输出

1

提示

　　找规律。

数据规模和约定

　　对于所有评测用例，1 <= N <= 1000000000。

解法一【错误解法】

package simulationMatch_12_2021_3;

import java.math.BigInteger;
import java.util.Scanner;

public class _07G {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		BigInteger fib[] = new BigInteger[10001];
		fib[1] = new BigInteger("1");
		fib[2] = new BigInteger("1");
		for (int i = 3; i <= 1000; i++) {
			fib[i] = fib[i - 1].add(fib[i - 2]);
			System.out.println(i + ": " + fib[i]);
		}
		if (fib[n].mod(new BigInteger("2")) != null) {
			System.out.println(1);
		} else {
			System.out.println(0);
		}
	}
//	public static void testLong() {
//		// System.out.println(Integer.MAX_VALUE);//2 147 483 647
//		Scanner sc = new Scanner(System.in);
//		int n = sc.nextInt();// 1 <= N <= 1 000 000 000
//		long fib[] = new long[1000];
//		fib[1] = 1l;
//		fib[2] = 1l;
//		for (int i = 3; i <= 100; i++) {
//			fib[i] = fib[i - 1] + fib[i - 2];
//			System.out.println(i + ": " + fib[i]);
//		}
//
//		if (fib[n] % 2 == 0) {
//			System.out.println(1);
//		} else {
//			System.out.println(0);
//		}
//	}
}

解法二

原文链接：1.0219——2021年第十二届蓝桥杯第三场校模拟赛

package simulationMatch_12_2021_3;

import java.util.Scanner;

public class _07G2 {
	public static void main(String[] args) {
		// 对于 50% 的评测用例，0 <= v < 10^9 (10的9次方)。
		// 对于所有评测用例， 0 <= v < 10^18 (10的18次方)。
		Scanner sc = new Scanner(System.in);
//		String str = sc.nextLine();
//		System.out.println(str);
		int n = sc.nextInt();
		if (n % 3 == 0) {
			System.out.println(0);
		} else {
			System.out.println(1);
		}
	}
}

八、试题H

问题描述

　　给定一个矩阵 M，由 n 行 m 列组成，第 i 行第 j 列值为 M[i][j]。
　　定义矩阵 M 的重量为矩阵中所有元素的和，几位weight(M)
　　请找到矩阵左上角的一个子矩阵S（矩阵的前 r 行中的前 c 列组成），使得这个子矩阵的重量的两倍最接近矩阵 M 重量。即 |2 weight(S)-weight(M)| 最小。
　　如果有多个子矩阵满足条件，请找出面积 r * c 最小的一个。
　　如果仍然有多个子矩阵满足条件，请找出其中 r 最小的一个。

输入格式

　　输入第一行包含两个整数 n, m，表示矩阵的大小。
　　接下来 n 行，每行 m 个整数，表示给定的矩阵M。

输出格式

　　输出一行，包含两个整数 r, c，表示子矩阵为矩阵 M 的前 r 行中的前 c 列。

样例输入

3 4
3 0 1 1
1 0 1 1
1 1 -2 4

样例输出

2 3

数据规模和约定

　　对于 30% 的评测用例，1 <= n, m <= 20, -10 <= M[i][j] <= 10。
　　对于 50% 的评测用例，1 <= n, m <= 100, -100 <= M[i][j] <= 100。
　　对于所有评测用例，1 <= n, m <= 1000, -1000 <= M[i][j] <= 1000。

解法一

原文链接：1.0219——2021年第十二届蓝桥杯第三场校模拟赛

package simulationMatch_12_2021_3;

import java.util.Scanner;

public class _08H {
	static int total = 0, n, m;
	static int[][] v;
	static int r = 0, c = 0, d = Integer.MAX_VALUE;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		m = sc.nextInt();
		v = new int[n][m];
		for (int i = 0; i < n; ++i) {
			for (int j = 0; j < m; ++j) {
				v[i][j] = sc.nextInt();
				total += v[i][j];
			}
		}
		int[][] dp = new int[n + 1][m + 1];
		for (int i = 1; i <= n; ++i) {
			for (int j = 1; j <= m; ++j) {
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + v[i - 1][j - 1];
				check(dp[i][j], i, j);
			}
		}
		System.out.println(r + " " + c);
	}

	public static void check(int x, int i, int j) {
		if (Math.abs(2 * x - total) < d || Math.abs(2 * x - total) == d && i * j < r * c) {
			r = i;
			c = j;
			d = Math.abs(2 * x - total);
		}
	}
}

九、试题I

问题描述

　　给定一张图片，由 n 行 m 列像素组成，每个像素由一个范围在 0 到 255 的整数表示。
　　例如，下面是一张 4 行 7 列的图片。
　　8 232 229 23 21 10 247
　　25 252 238 17 241 9 245
　　1 243 251 32 236 31 253
　　13 5 255 8 13 24 11
　　对于每个像素，请找出以这个像素为中心的3行3列中最亮（数值最大）的像素值。
　　例如，第 2 行第 2 列像素值为 252，而它周围 8 个像素都没有它亮，因此第 2 行第 2 列对应的值为 252。
　　第 3 行第 2 列对应的值为255。
　　第 1 行第 1 列为中心不足 3 行 3 列，最大值为 252。
　　将每个像素对应的值写成上面图片的样子，得到：
　　252 252 252 241 241 247 247
　　252 252 252 251 241 253 253
　　252 255 255 255 241 253 253
　　243 255 255 255 236 253 253

输入格式

　　输入第一行包含两个整数 n, m，分别表示图片的行数和列数。
　　接下来 n 行，每行 m 个整数，表示一个像素。

输出格式

　　输出 n 行，每行 m 个整数，表示以每个像素为中心的3行3列中最亮的像素值。

样例输入

4 7
8 232 229 23 21 10 247
25 252 238 17 241 9 245
1 243 251 32 236 31 253
13 5 255 8 13 24 11

样例输出

252 252 252 241 241 247 247
252 252 252 251 241 253 253
252 255 255 255 241 253 253
243 255 255 255 236 253 253

数据规模和约定

　　对于所有评测用例，图片的行数和列数均不超过 100，每个像素的值为 0 到 255 之间的整数。

解法一

求巨佬支招！

九、试题I（2）

时间限制: 3.0s 内存限制: 512.0MB 本题总分：25 分

【问题描述】
杂货铺老板一共有N件物品，每件物品具有ABC三种属性中的一种或多种。从杂货铺老板处购得一件物品需要支付相应的代价。
现在你需要计算出如何购买物品，可以使得ABC三种属性中的每一种都在至少一件购买的物品中出现，并且支付的总代价最小。

【输入格式】
输入第一行包含一个整数N。
以下N行，每行包含一个整数C和一个只包含"ABC"的字符串，代表购得该物品的代价和其具有的属性。

【输出格式】
输出一个整数，代表最小的代价。如果无论如何凑不齐ABC三种属性，输出-1。

【样例输入】
5
10 A
9 BC
11 CA
4 A
5 B

【样例输出】
13

【评测用例规模与约定】
对于50%的评测用例，1 <= N <= 20
对于所有评测用例，1 <= N <= 1000， 1 <= C <= 100000

解法一

原文链接：1.0219——2021年第十二届蓝桥杯第三场校模拟赛

package simulationMatch_12_2021_3;

//这种写法更简单同时效率更高
import java.util.Arrays;
import java.util.Scanner;

public class _09I2 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int[] dp = new int[7 + 1]; // 模拟二进制，三种属性C、B、A，让它们分别代表4、2、1，即1<<2、1<<1、1<<0（注1<

十、试题J

问题描述

　　给定一个序列 (a_1, a_2, ..., a_n), 它的一个上升子序列是指从序列中取出一些元素，按照原来的顺序排列后，是单调递增的序列。
　　例如，对于序列 (3, 2, 7, 6, 7)，取出下标为 2, 4, 5 的元素 a_2, a_4, a_5，即 2, 6, 7，是一个上升子序列。
　　在这个序列中，有 7 个长度为 2 的上升子序列，例如
　　1. 下标 1, 3 对应的 3, 7；
　　2. 下标 1, 4 对应的 3, 6；
　　3. 下标 1, 5 对应的 3, 7；
　　4. 下标 2, 3 对应的 2, 7；
　　5. 下标 2, 4 对应的 2, 6；
　　6. 下标 2, 5 对应的 2, 7；
　　7. 下标 4, 5 对应的 6, 7。
　　注意，可能有下标不同但对应数值相同的上升子序列，他们应当算成不同的上升子序列。
　　给定序列，请问序列中一共有多少个长度为 k 的上升子序列。

输入格式

　　输入第一行包含两个整数 n, k，表示序列的长度和上升子序列的长度。
　　第二行包含 n 个整数 a_1, a_2, ..., a_n，表示给定的序列。

输出格式

　　输出一行，包含一个整数，表示长度为 k 的上升子序列的数量，答案可能很大，请输出答案除以 1000007 的余数。

样例输入

5 2
3 2 7 6 7

样例输出

7

数据规模和约定

　　对于 30% 的评测用例，1 <= n <= 20, 0 <= a_i <= 100。
　　对于 50% 的评测用例，1 <= n <= 100, 0 <= a_i <= 1000。
　　对于所有评测用例，1 <= n <= 1000, 1 <= k <= 10, 0 <= a_i <= 10000。

解法一

原文链接：1.0219——2021年第十二届蓝桥杯第三场校模拟赛

package simulationMatch_12_2021_3;

import java.util.Scanner;
import java.util.Arrays;

public class _10J {
	static int n, k, MOD = 1000007;
	static int[] r;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt();
		k = sc.nextInt();
		r = new int[n];
		for (int i = 0; i < n; ++i) {
			r[i] = sc.nextInt();
		}
		int[][] dp = new int[n][k + 1];
		for (int i = 0; i < n; ++i) {
			dp[i][1] = 1;
		}
		for (int i = 1; i < n; ++i) {
			for (int j = 0; j < i; ++j) {
				if (r[i] > r[j]) {
					for (int t = 1; t <= k; ++t) {
						if (dp[j][t - 1] != 0) {
							dp[i][t] = (dp[i][t] + dp[j][t - 1]) % MOD;
						}
					}
				}
			}
		}
		int ans = 0;
		for (int i = 0; i < n; ++i) {
			ans = (ans + dp[i][k]) % MOD;
		}
		System.out.println(ans);
	}
}

小结

难！