【聚类分析】基于matlab GUI K-means聚类分析【含Matlab源码 791期】
一、简介
1 聚类分析
聚类:
把相似数据并成一组(group)的方法。‘物以类聚,人以群分’
不需要类别标注的算法,直接从数据中学习模式
所以,聚类是一种 数据探索 的分析方法,他帮助我们在大量数据中探索和发现数据结构
1.1 相似度与距离度量
定义距离来度量表示相似度:
欧式距离,曼哈顿距离,闵氏距离
距离与变量量纲的关系
变量标准化方法:
0-1 标准化
区间缩放法 (a,b)=(0,1)
类别变量onehot
1.2 聚类算法及划分方法
常见的两类聚类算法:
层次聚类算法(Hierarchical)
基于划分的方法(Partitional)
基于密度 和 基于模型
基于划分的方法(Partitional):K-means(K均值)
1 随机选取K个数据点作为‘种子’
2 根据数据点与‘种子’的距离大小进行类分配
3 更新类中心点的位置,以新的类中心点作为‘种子’
4 按照新的‘种子’对数据归属的类进行重新分配
5 更新类中心点(–>3–>4),不断迭代,直到类中心点变得很小
2 聚类模型评估(优缺点)
优点: 算法原理简单,处理快
当聚类密集时,类与类之间区别明显,效果好
缺点: K是事先给定的,K值选定难确定
对孤立点、噪声敏感
结果不一定是全局最优,只能保证局部最优。
很难发现大小差别很大的簇及进行增量计算
结果不稳定,初始值选定对结果有一定的影响
计算量大
3 K-means 在 sklearn方法
sklearn.cluster.KMeans(
n_clusters = 8, #聚类个数,K值,默认8
init = 'k-means++',
n_init = 10,
max_iter = 300,
tol = 0.0001,
precompute_distances = 'auto',
verbose = 0,
random_state = None,
copy_x = True,
n_jobs = 1,
algorithm = 'auto'
)
一些重要的参数:
n_clusters = 8, #聚类个数,K值,默认8
init = 'k-means++', #初始化类中心点选择方法,可选:
{
'k-means++', #是一种优化选择方法,比较容易收敛
'random', #随机选择
an ndarray #可以通过输入ndarray数组手动指定中心点
}
max_iter: #最大迭代数
precompute_distances: #预计算距离,计算速度更快但占用更多内存。auto True
copy_x # True,原始数据不变,False直接在原始数据上做更改
4 确定K值–肘部法则–SSE
最合适的K值
肘部法则(Elbow method):找到随着K值变大,损失函数的拐点。
损失函数:各个类畸变程度(distortions)之和
SSE是每个属性的SSE之和:
1. 对于所有的簇,某变量的SSE都很低,都意味着什么?
2. 如果只对一个簇很低,意味着什么?
3. 如果只对一个簇很高,意味着什么?
4. 如果对所有簇都很高,意味着什么?
5. 如何使用每个变量的SSE信息改进聚类?
解答: 1. 说明该属性本质上为常量,不能作为聚类依据。
2. 那么该属性有助于该簇的定义
3. 那么该属性为噪声属性
4. 那么该属性 与 定义该属性提供的信息不一致,也意味着该属性不利于簇的定义。
5. 消除对于所有簇都是 低的SSE(高的SSE)的属性。因为这些属性对聚类没有帮助,
这些属性在SSE的总和计算中引入了噪声。
也可以对其中某些属性用加权概率来计算,使该属性有助于该簇的定义,
去除某些不利于该簇定义的影响因子(那些可能是噪声)。从而更有利于簇的聚类。
K-means 附加问题
1.处理空簇:如果数据量少,寻找替补质心,使SSE最小。如果数据量大,保留该空簇
2.离群点:不能删除。建议聚类之前离群检测。分析看能否删除
3.降低SSE :将大的分散的簇再次拆开;引入新的簇将之前的大簇拆分。
4.增量更新质心:再次在质心附近寻找测试点,看能否再次找到更优的质心。

5 模型评估指标–轮廓系数法–最近簇
聚类目的是让“组内数据尽量相似”,而“组间数据差异明显”,轮廓系数就是衡量方法。
针对每一条数据i
a(i)数据i与组内其它数据的平均距离
b(i)数据i与邻组的数据的平均距离
5.1 轮廓系数

5.2 最近簇定义—平均轮廓系数 [0,1]:
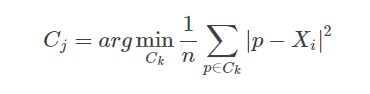
其中p是某个簇Ck中的样本。即,用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后,
选择离Xi最近的一个簇作为最近簇。
sklearn.metrics.silhouette_score
sklearn.metrics.silhouette_score(
X,
labels = 'euclidean',
sample_size = None,
random_state = None
)
一些重要的参数:
X: 聚类的输入特征数据
labels:类标签数组
metrics:
sample_size:是否抽样计算
5.3、Canopy算法配合初始聚类
1.聚类最耗费计算的地方是计算对象相似性的时候,Canopy聚类在第一阶段选择简单、
计算代价较低的方法计算对象相似性,将相似的对象放在一个子集中,这个子集被叫做Canopy ,
通过一系列计算得到若干Canopy,Canopy之间可以是重叠的,但不会存在某个对象不属于任何Canopy的情况,
可以把这一阶段看做数据预处理;
2.在各个Canopy 内使用传统的聚类方法(如K-means),不属于同一Canopy 的对象之间不进行相似性计算。
(即,根据Canopy算法产生的Canopies代替初始的K个聚类中心点,
由于已经将所有数据点进行Canopies有覆盖划分,
在计算数据离哪个k-center最近时,不必计算其到所有k-centers的距离,
只计算和它在同一个Canopy下的k-centers这样可以提高效率。
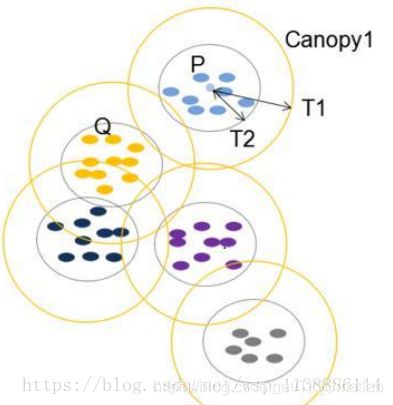
算法过程:
1,首先选择两个距离阈值:T1和T2,其中T1 > T2
2,从list中任取一点P,用低计算成本方法快速计算点P与所有Canopy之间的距(如果当前不存在Canopy,则把点P作为一个Canopy),如果点P与某个Canopy距离在T1以内,则将点P加入到这个Canopy
3,如果点P曾经与某个Canopy的距离在T2以内,则需要把点P从list中删除,这一步是认为点P此时与这个Canopy已经够近了,因此它不可以再做其它Canopy的中心了;
4,重复步骤2、3,直到list为空结束。
优缺点
1、Kmeans对噪声抗干扰较弱,通过Canopy对比,将较小的NumPoint的Cluster直接去掉有利于抗干扰。
2、Canopy选择出来的每个Canopy的centerPoint作为K会更精确。
3、只是针对每个Canopy的内做Kmeans聚类,减少相似计算的数量。
二、源代码
function KmeansMain
close all;clear;clc;
%随机生成随机数
mu = [0 0];
%协方差矩阵,对角为方差值0.3,0.35
var = [0.3 0; 0 0.35];
samNum = 200;
data = mvnrnd(mu, var, samNum);
a = figure;
plot(gca, data(:,1), data(:,2), '*', 'color', 'k');hold on;
classNum = [];%类数
iterNum = 0;%迭代次数
x = [];
centerPoint = [];
centerPointPathAarry = [];
h_plotCenterPoint = [];%中心点绘制handle
h_plotPath = [];%中心点路径绘制handle
%centerPointPathAarry结构
%第1次迭代|中心点1(x,y)|中心点2(x,y)|中心点3(x,y)|中心点n(x,y)
%第2次迭代|中心点1(x,y)|中心点2(x,y)|中心点3(x,y)|中心点n(x,y)
h_slider = uicontrol(a,'Style', 'slider',...
'SliderStep',[0.02 0.02],...
'Min',0,'Max',50,'Value',0,...
'Position', [400 20 100 20],...
'Callback', {
@classify,gca});
h_edit = uicontrol(a,'Style', 'edit',...
'String', '200',...
'Position', [80 20 40 20],...
'Callback', {
@paintRandomPoint,gca});
uicontrol('Style', 'popup',...
'String', '自定义|随机2点|随机3点|随机4点',...
'Position', [200 22 120 20],...
'Callback', {
@SpsfPoit,gca});
h_t1 = uicontrol('Style','text','String','迭代', ...
'Position', [355 20 40 20]);
h_textClassNum = uicontrol('Style','text','String','中心点', ...
'Position', [140 20 55 20]);
uicontrol('Style','text','String','样本点数:', ...
'Position', [25 20 50 20]);
h_textshow = uicontrol('Style','text','String','0','Position', [500 20 20 20]);
set(gca,'xtick',[],'ytick',[],...
'title',text('string','Kmeans演示脚本','color','k'));
xlim([-1.5 1.5]);ylim([-1.5 1.5]);
%%%%%%%%%%%%%%%%%%%%
function SpsfPoit(hObj,event,ax)
set(h_slider,'value',0); %清零滑动条,以实现从0迭代
cla;%清空axes
set(h_textshow,'string',0);%界面显示的迭代次数清零
%句柄赋值为空
h_plotCenterPoint = [];
h_plotPath = [];
centerPointPathAarry = [];%轨迹归零
plot(gca, data(:,1), data(:,2), '*', 'color', 'k');%样本点颜色初始化
val = get(hObj, 'Value');%获得popup menu的值
if val == 1
%选择任意若干点作为中心点
[x, y] = ginput;
centerPoint = [x y];
[classNum, ~] = size(centerPoint);
repaintBeginPoint(h_plotCenterPoint, classNum, centerPoint);
elseif val == 2
%选择任意2点作为中心点
centerPoint = rand(2, 2)*2-0.5;
[classNum, ~] = size(centerPoint);
repaintBeginPoint(h_plotCenterPoint, classNum, centerPoint);
elseif val == 3
%选择任意3点作为中心点
centerPoint = rand(3, 2)*2-0.5;
[classNum, ~] = size(centerPoint);
repaintBeginPoint(h_plotCenterPoint, classNum, centerPoint);
elseif val == 4
%选择任意4点作为中心点
centerPoint = rand(4,2)*2-0.5;
[classNum,~] = size(centerPoint);
repaintBeginPoint(h_plotCenterPoint, classNum, centerPoint);
end
[labelSample] = classifyAndShowAndLabel(classNum, centerPoint, data, samNum, gca);
centerPointPathAarry = [centerPointPathAarry; reshape(centerPoint', 1, classNum*2)];
set(h_textClassNum, 'string', [num2str(classNum) '个中心点']);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%迭代分类函数%%%%%%%%%%%%%%%%%%%%
function classify(hObj,event,ax)
iterNum = round(get(hObj, 'value'));
set(h_textshow, 'string', iterNum);
%根据起始点分类,并且为不同的类标记不同颜色,返回带标签样本数据
[labelSample] = classifyAndShowAndLabel(classNum, centerPoint, data, samNum, gca);
%重新获得起始点矩阵centerPoint(x|y)
[centerPoint] = recalClassCenter(labelSample, classNum);
centerPointPathAarry = [centerPointPathAarry; reshape(centerPoint', 1, classNum*2)];
%重新绘制起始点centerPoint(x|y)到axes上
repaintBeginPoint(h_plotCenterPoint, classNum, centerPoint);
disp('path:');
disp(centerPointPathAarry);%将中心点的轨迹显示出来
for i = 1:classNum
[selected_color] = colorMap(i, classNum);
h_plotPath(i)=plot(centerPointPathAarry(:, (i*2)-1), centerPointPathAarry(:,i*2), 'color', selected_color);
end
end
%%%%%%%%%%%%%%%函数部分%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%重新绘制起始点函数%%%%%%%%%
function repaintBeginPoint(handle_plo,classnum,R)
delete(h_plotCenterPoint);%清除绘制的中心点,并将句柄赋值为空
h_plotCenterPoint=[];
%重新绘制起始点,每个起始点的颜色不同
for i = 1:classnum
[selected_color] = colorMap(i, classnum);
h_plotCenterPoint(i) = plot(R(i,1), R(i,2), 'o', 'MarkerSize', 7, 'MarkerFaceColor', selected_color);
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%重新计算类重心%%%%%%%%%%%%%%%%%%%%%%
function [newCenterPoint]=recalClassCenter(labelSample,classNum)
%R为重新被计算的类中心
newCenterPoint=[];
%分类并且计算每个类的重心
for i=1:classNum
%取出所有标签为i类的所有行,即第i类的所有点
classs=labelSample(labelSample(:,3)==i,:);
%有用的只有第一列和第二列,去除标签列
classs=[classs(:,1),classs(:,2)];
%重新计算重心
classs_repoint=mean(classs);
newCenterPoint=[newCenterPoint;classs_repoint];
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%根据起始点分类,并且为不同的类标记不同颜色,返回带标签样本数据%%%%%%%%%
function [labelSample]=classifyAndShowAndLabel(classNum,centerPoint,data1,samNum,gca)
disArray=[];
for i=1:classNum
calproA=[centerPoint(i,:);data1(:,1),data1(:,2)];
Adist=pdist(calproA,'euclidean');
Adist=Adist(1:samNum)';
disArray=[disArray,Adist];
end
%拼接,得到距离矩阵,一列代表一个点到所有样本点的距离
%disArray=[Adist Bdist];
%disp(disArray);
%获取每一行最小值所在距离矩阵的列
%并和原样本矩阵拼接为labelSample
%labelSample 表示被标记的原始样本,每一行为一个样本
%每一行的最后一列为标记值,在这里标记是距离哪个样本点最近。
minn=min(disArray');
cols=[];
for i=1:length(minn)
[row,col] = find(disArray==minn(i));
cols(i)=col;
end
cols=cols';
labelSample=[data1(:,1),data1(:,2),cols];
%将不同类的点标上不同的颜色
for i=1:samNum
[selected_color]=colorMap(labelSample(i,3),classNum);
plot(gca,data1(i,1),data1(i,2),'*','color',selected_color);
end
end
三、运行结果
四、备注
完整代码或者代写添加QQ 1564658423