一、堆的定义
(1)堆树是一颗完全二叉树;
(2)堆树中某个节点的值总是不大于或不小于其孩子节点的值;
(3)堆树中每个节点的子树都是堆树。
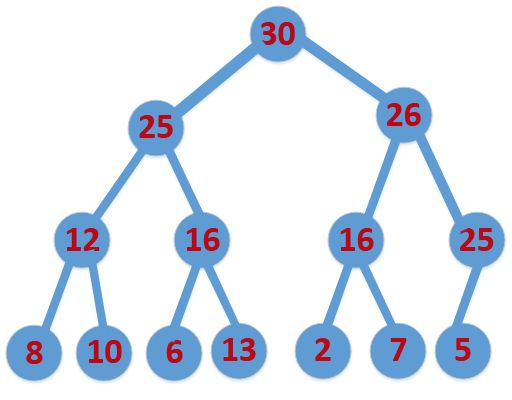
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。
当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。
最大堆和最小堆的用法类似,仅仅是把代码中的大于号换成小于号就可以完成转换。
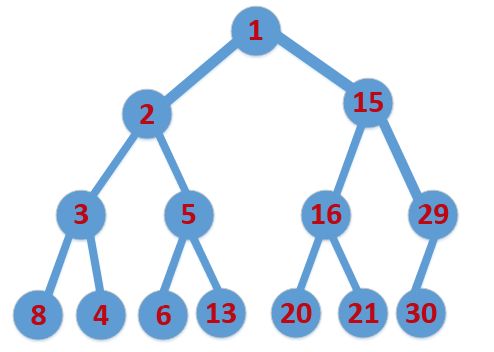
这里,我们以最小堆为例:
我们也可以把他放在一个数组中:
[0]=1 [1]=2 [2]=15 [3]=3 [4]=5 [5]=16 [6]=29 [7]=8 [8]=4 [9]=6 [10]=13 [11]=20 [12]=21 [13]=30
所以数组也是一颗完全二叉树。
二、构建堆
给定一个数组:int [] array = {8 ,3 ,20 ,2 ,5 ,15 ,29 ,1 ,4 ,6 ,13 ,16 ,21 ,30};
我们需要把他转换成一个堆,按照定义中的三点,数组已经符合了第一条
按照定义中的第二点,堆树中某个节点的值总是不大于或不小于其孩子节点的值,由于我们需要构建的是最小堆,所以某个点的值不大于其孩子的值,当不满足条件时,我们就交换节点和孩子的值。
代码实现:
//从根开始向下调整
public static void shiftDown(int index,int [] array,int len)
{
int tmpIndex = 0;
while (index <= (len - 2 -1)/2)
{
//左孩子和右孩子先比较,小的一个再和父节点比较,如果父节点大于孩子节点,那么父节点和孩子交换
tmpIndex = (array[2 * index + 1] > array[2 * index + 2]) ? (2 * index + 2) : (2 * index + 1);//找到左孩子、右孩子中值小的一个
if (array[tmpIndex] < array[index]) //孩子的值比根的值小
{
swap(tmpIndex,index,array);//交换两个值
index = tmpIndex;//把序号赋值后继续下一轮循环
}else {
break;
}
}
}
//交换两个值
private static void swap(int indexA,int indexB,int [] array)
{
int tmp = array[indexA];
array[indexA] = array[indexB];
array[indexB] = tmp;
}
按照堆定义的第三点,堆树中每个节点的子树都是堆树,所以我们可以依次从堆数的右下角开始调整个完全二叉树中的所有节点,那么整个完全二叉树就变成了堆。
代码实现:
//生成一个堆
public static void createHeap(int [] array)
{
int len = array.length;
for (int i = len / 2;i >= 0 ; i --)
{
shiftDown(i,array,len);
//System.out.print(i + ": ");
//printArray(array);
}
}
三、堆排序
按照堆的特新,在最小堆中,根就是最小值,那么我们先取出根,再调整整个堆,又取出最小堆中的根,那么依次取出的值就是排好序的了。
当然在实际生产中,我们是用根和堆最后一个数交换的
交换前:[0]=1 [1]=2 [2]=15 [3]=3 [4]=5 [5]=16 [6]=29 [7]=8 [8]=4 [9]=6 [10]=13 [11]=20 [12]=21 [13]=30
交换后:[0]=30 [1]=2 [2]=15 [3]=3 [4]=5 [5]=16 [6]=29 [7]=8 [8]=4 [9]=6 [10]=13 [11]=20 [12]=21 [13]=1
这个时候我们只需要调整0~12的元素就可以了,把它调整为最小堆,
调整后:[0]=2 [1]=3 [2]=15 [3]=4 [4]=5 [5]=16 [6]=29 [7]=8 [8]=30 [9]=6 [10]=13 [11]=20 [12]=21 [13]=1
交换一次需要调整的长度就减少1,一直调整到只剩下根节点的时候就不需要调整了。
代码实现:
public static void heapSort(int [] array)
{
createHeap(array);
for (int i = 0;i < array.length ; i++)
{
//arrar[0]项是最小的,第一项arrar[0]和最后一项arrar[array.length -1]交换,当前堆最小值就放到了数组末尾,也就是堆得右下角
//之前末尾的项背长度变成了之前长度减一,这时候堆顶的数值为之前arrar[array.length -1]中的值,需要调整的长度变成array.length -1,
//再用shiftDown方法调整使其为堆
//printArray(array);
swap(0,array.length - i -1,array);
shiftDown(0,array,array.length - 1- i);
}
}
完整代码:
public class HeapUtils {
//从根开始向下调整
public static void shiftDown(int index,int [] array,int len)
{
int tmpIndex = 0;
while (index <= (len - 2 -1)/2)
{
//左孩子和右孩子先比较,小的一个再和父节点比较,如果父节点大于孩子节点,那么父节点和孩子交换
tmpIndex = (array[2 * index + 1] > array[2 * index + 2]) ? (2 * index + 2) : (2 * index + 1);//找到左孩子、右孩子中值小的一个
if (array[tmpIndex] < array[index]) //孩子的值比根的值小
{
swap(tmpIndex,index,array);//交换两个值
index = tmpIndex;//把序号赋值后继续下一轮循环
}else {
break;
}
}
}
//从底部向上调整
public static void shiftUp(int index,int [] array,int len)
{
if (index == 0)//如果已经是第一个了就不需要继续向上调整
{
return;
}
while (index -2 >= 0)
{
//和孩子节点和父节点比较,如果父节点 大于 孩子 那么就交换
//(2 *k - 2)= index => k = (index - 2)/2
if ((array[(index - 2)/2] > array[index])){
swap((index - 2)/2,index,array);
index = (index - 2)/2;
}else {
break;
}
}
}
//交换两个值
private static void swap(int indexA,int indexB,int [] array)
{
int tmp = array[indexA];
array[indexA] = array[indexB];
array[indexB] = tmp;
}
//生成一个堆
public static void createHeap(int [] array)
{
int len = array.length;
for (int i = len / 2;i >= 0 ; i --)
{
shiftDown(i,array,len);
//System.out.print(i + ": ");
//printArray(array);
}
}
public static void createHeap1(int [] array)
{
int len = array.length;
for (int i = 0; i < len ; i++)
{
shiftUp(i,array,i + 1);
}
}
public static void printArray(int [] array)
{
System.out.print("数组:");
for (int i = 0 ; i < array.length ; i++)
{
System.out.print( "["+ i + "]=" + array[i] + " ");
}
System.out.println("");
}
public static void heapSort(int [] array)
{
createHeap(array);
for (int i = 0;i < array.length ; i++)
{
//arrar[0]项是最小的,第一项arrar[0]和最后一项arrar[array.length -1]交换,当前堆最小值就放到了数组末尾,也就是堆得右下角
//之前末尾的项背长度变成了之前长度减一,这时候堆顶的数值为之前arrar[array.length -1]中的值,需要调整的长度变成array.length -1,
//再用shiftDown方法调整使其为堆
//printArray(array);
swap(0,array.length - i -1,array);
shiftDown(0,array,array.length - 1- i);
}
}
}
public class HeapMain {
public static void main(String[] args) {
int [] array = {8 ,3 ,20 ,2 ,5 ,15 ,29 ,1 ,4 ,6 ,13 ,16 ,21 ,30};
HeapUtils.printArray(array);
HeapUtils.createHeap(array);
System.out.println("堆:");
HeapUtils.printArray(array);
System.out.println("排序后:");
HeapUtils.heapSort(array);
HeapUtils.printArray(array);
}
}
结果:
时间复杂度分析
初始化建堆
初始化建堆只需要对二叉树的非叶子节点调用shiftDown()函数,由下至上,由右至左选取非叶子节点来调用shiftDown()函数。那么倒数第二层的最右边的非叶子节点就是最后一个非叶子结点。
假设高度为k,则从倒数第二层右边的节点开始,这一层的节点都要执行子节点比较然后交换(如果顺序是对的就不用交换);倒数第三层呢,则会选择其子节点进行比较和交换,如果没交换就可以不用再执行下去了。如果交换了,那么又要选择一支子树进行比较和交换;高层也是这样逐渐递归。
那么总的时间计算为:s = 2^( i - 1 ) * ( k - i );其中 i 表示第几层,2^( i - 1) 表示该层上有多少个元素,( k - i) 表示子树上要下调比较的次数。
S = 2^(k-2) * 1 + 2(k-3)2…..+2(k-2)+2(0)*(k-1) ===> 因为叶子层不用交换,所以i从 k-1 开始到 1;
这个等式求解:等式左右乘上2,然后和原来的等式相减,就变成了:
S = 2^(k - 1) + 2^(k - 2) + 2^(k - 3) ..... + 2 - (k-1)
除最后一项外,就是一个等比数列了,直接用求和公式:
S = 2^k -k -1;又因为k为完全二叉树的深度,所以n = 2 ^k => log(n) =k,把此式带入
得到:S = n - log(n) -1,所以时间复杂度为:O(n)
排序重建堆
在取出堆顶点放到对应位置并把原堆的最后一个节点填充到堆顶点之后,需要对堆进行重建,只需要对堆的顶点调用adjustheap()函数。
每次重建意味着有一个节点出堆,所以需要将堆的容量减一。shiftDown()函数的时间复杂度k=log(n),k为堆的层数。所以在每次重建时,随着堆的容量的减小,层数会下降,函数时间复杂度会变化。重建堆一共需要n-1次循环,每次循环的比较次数为log(i),则相加为:log2+log3+…+log(n-1)+log(n)≈log(n!)。可以证明log(n!)和nlog(n)是同阶函数:
∵(n/2)n/2≤n!≤nn,∵(n/2)n/2≤n!≤nn,
∴n/4log(n)=n/2log(n1/2)≤n/2log(n/2)≤log(n!)≤nlog(n)∴n/4log(n)=n/2log(n1/2)≤n/2log(n/2)≤log(n!)≤nlog(n)
所以时间复杂度为O(nlogn)
空间复杂度
因为堆排序是就地排序,空间复杂度为常数:O(1)
算法稳定性
堆排序是一种不稳定的排序方法。因为在堆的调整过程中,关键字进行比较和交换所走的是该结点到叶子结点的一条路径,因此对于相同的关键字就可能出现排在后面的关键字被交换到前面来的情况。