机器学习 线性回归法（Linear Regression）与梯度下降法（Gradient Descent）

希望阅读本文可以从头开始看，博主自认为保持着逻辑连贯性
机器学习算法分为分类算法和回归算法，这一章节学习的是线性回归法，通过学习线性回归法可以对机器学习的过程有一个很好的认知，同时梯度下降法并不是一种机器学习方法，但结合线性回归法可以很好的理解。

1 线性回归理论推导

当我们拿到样本数据集时，线性回归法的任务就是寻找一条直线，最大程度的拟合样本特征和样本输出标记之间的关系，回归问题的输出标记要使用一个坐标轴。

这里我们从最简单的情况入手，假设样本只有一个样本特征时，这时称为简单回归算法。假设我们找到了最佳拟合的直线方程：$$y=ax+b$$则对于每个样本点$x^{(i)}$来说，根据我们的直线方程，预测值为：$${\hat{y}}^{(i)}=a{x}^{(i)}+b$$我们把样本$x^{(i)}$的真正的样本输出记作$y^{(i)}$，这时我们的问题可以换一种形式，即我们希望$y^{(i)}$和${\hat{y}}^{(i)}$的差距尽量小，这样我们就需要一种数学方式去表达$y^{(i)}$和${\hat{y}}^{(i)}$的差距，于是我们有了下面几种形式：$$y^{(i)}-{\hat{y}}^{(i)}$$$$|y^{(i)}-{\hat{y}}^{(i)}|$$$$(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$这里上面的三种方法看似都是合理的，实质上在往下计算上由很大的差距，第一个式子会产生结果正负无法求和的问题，第二个式子为绝对值函数，但绝对值函数并不是处处可导的，所以我们最后选择的是第三个式子，考虑到所有样本为：$$\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$这样我们就可以把问题化为一个数学目标，我们的目标是使下式尽可能的小：$$J(a,b)=\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-b{)}^2$$当上式足够小时的a和b就是我们寻找的目标。上面的函数$J(a,b)$被称为损失函数(loss function)相对还有效用函数(utility function)，通过上面简单的推导，你需要知道的是近乎所有的参数学习算法都是这样的套路，通过分析问题，确定问题的损失函数或效用函数，通过最优化损失函数或效用函数，获得机器学习的模型。 对于不同问题最优化损失函数和效用函数的求解不同问题有着不同的解法。

对于线性回归算法的损失函数来说，最优化是一个典型的最小二乘法问题：最小化误差的平方。下面就是我运用最小二乘法来推导出a,b的过程。$$J(a,b)=\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-b{)}^2$$$$令\frac{\partial J(a,b)}{\partial a}=0与\frac{\partial J(a,b)}{\partial b}=0$$这里b之前的系数为1比较简单，就先来计算b的偏导数：$$\frac{\partial J(a,b)}{\partial b}=\sum _{i=1}^{m}2(y^{(i)}-a{x}^{(i)}-b)(-1)=0$$上式化为$$\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-b)=0$$$$\sum _{i=1}^m{y}^{(i)}-a\sum _{i=1}^m{x}^{(i)}-\sum _{i=1}^{m}b=0$$$$\sum _{i=1}^m{y}^{(i)}-a\sum _{i=1}^m{x}^{(i)}-mb=0$$$$mb=\sum _{i=1}^m{y}^{(i)}-a\sum _{i=1}^m{x}^{(i)}$$可得到$$b=\overline{y}-a\overline{x}$$就此我们得到了b的值，下面计算a的偏导：$$\frac{\partial J(a,b)}{\partial a}=\sum _{i=1}^{m}2(y^{(i)}-a{x}^{(i)}-b)(-x^{(i)})=0$$$$\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-b)x^{(i)}=0$$这里我们把上面求出的b代入式中：$$\sum _{i=1}^m(y^{(i)}-a{x}^{(i)}-\overline{y}+a\overline{x})x^{(i)}=0$$$$\sum _{i=1}^m(x^{(i)}{y}^{(i)}-a(x^{(i)}{)}^2-x^{(i)}\overline{y}+a\overline{x}{x}^{(i)})=0$$$$\sum _{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})-a\sum _{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})=0$$可得到$$a=\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)})}$$如果推导到这里其实已经可以编程实现了，但对于计算机来说这还不是最简单的结果，下面就是体现数学的魅力的时候了，观察上式中分子中${\sum }_{i=1}^m{x}^{(i)}\overline{y}$，我们对其进行变形：$$\sum _{i=1}^m{x}^{(i)}\overline{y}=\overline{y}\sum _{i=1}^m{x}^{(i)}=m\overline{y}\cdot \overline{x}=\overline{x}\sum _{i=1}^m{y}^{(i)}=\sum _{i=1}^m\overline{y}\cdot \overline{x}$$这样我们对a的结果进一步化简：$$a=\frac{{\sum }_{i=1}^m(x^{(i)}{y}^{(i)}-x^{(i)}\overline{y}-\overline{x}{y}^{(i)}+\overline{x}\cdot \overline{y})}{{\sum }_{i=1}^m((x^{(i)}{)}^2-\overline{x}{x}^{(i)}-\overline{x}{x}^{(i)}+{\overline{x}}^2)}$$注意这里分子分母上下都用了上面的变形技巧添加了两项，之后a就可化为：$$a=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2}$$可能看到这个结果你会认为这个结果与上面没有化简之前的结果数量级是一样的，但如果你仔细观察这个结果你就会发现它是极易实现向量化的，使用向量化运算会比最开始的结果快50倍左右，下面小节中可以看到结果。现在我们有了a和b的值，我们可以自己去实现自己的线性回归模型啦！

2 简单线性回归的实现

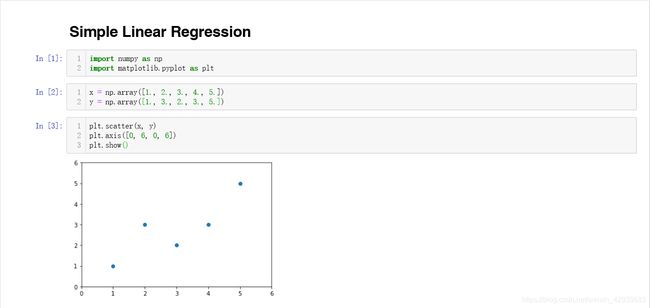
我们创建一组简单的数据来模拟回归的过程：

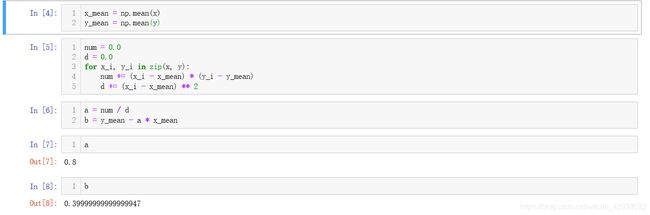
下面我们用上一小节推出的公式，来完成参数a和b的计算：

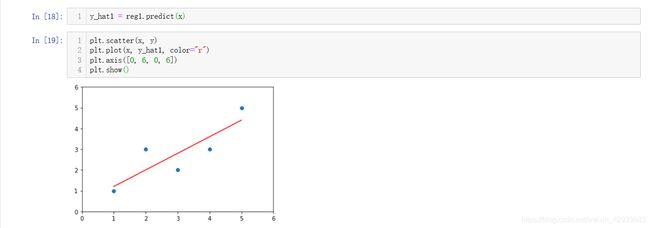
将我们的样本点和计算出的回归直线画出来：

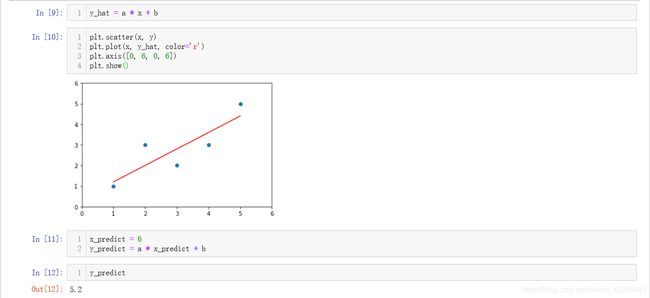
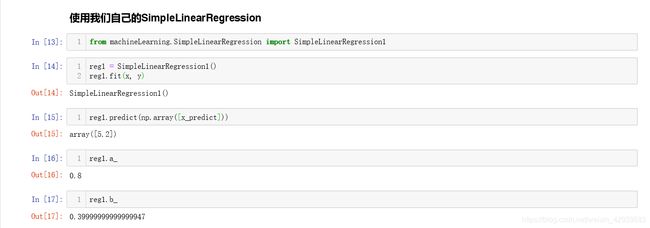
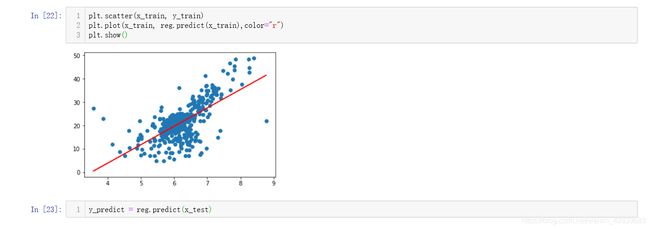
到这里就是简单线性回归的整个过程，我们使用如Scikit-learn中建模规则来创建属于我们自己的简单线性回归模型：

import numpy as np

class SimpleLinearRegression1:

    def __init__(self):
        """初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集训练Simple Linear Regression"""
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train."
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = 0.0
        d = 0.0
        for x,y in zip(x_train, y_train):
            num += (x - x_mean) * (y - y_mean)
            d += (x - x_mean) ** 2

        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集，返回结果向量"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data"
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single， 返回x_single的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression1()"

下面创建我们自己的模型：

整个过程上下得到的结果都没有改变，只不过希望大家可以明白调用Scikit-learn中模型的过程与其模型中的结构，包含init，fit，predict方法。在第一小节中有一个数学上对a的化简，当时我说的这个化简会对运算减少很多的时间，接下来这一小节让我们来看一下衡量线性回归的指标。

3 衡量线性回归的指标

在第一小节中我们把a化为了下面的形式：$$a=\frac{{\sum }_{i=1}^m(x^{(i)}-\overline{x})(y^{(i)}-\overline{y})}{{\sum }_{i=1}^m(x^{(i)}-\overline{x}{)}^2}$$对于上式来说，分子分母都是对应向量对应项相乘，所以我们就可以把它化为向量的形式：$$a=\frac{{\sum }_{i=1}^m{w}^{(i)}\cdot v^{(i)}}{{\sum }_{i=1}^m{w}^{\prime (i)}\cdot v^{\prime (i)}}=\frac{w\cdot v}{w^{\prime }\cdot v^{\prime }}$$这样从程序中实现会加快多少倍呢？

上一小节我们使用for循环创建SimpleLinearRegression1，这里我们用向量化创建SimpleLinearRegression2:

class SimpleLinearRegression2:

    def __init__(self):
        """初始化Simple Linear Regression 模型"""
        self.a_ = None
        self.b_ = None

    def fit(self, x_train, y_train):
        """根据训练数据集训练Simple Linear Regression"""
        assert x_train.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data."
        assert len(x_train) == len(y_train), \
            "the size of x_train must be equal to the size of y_train."
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)

        num = (x_train - x_mean).dot(y_train - y_mean)
        d = (x_train - x_mean).dot(x_train - x_mean )


        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean

        return self

    def predict(self, x_predict):
        """给定待预测数据集，返回结果向量"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only solve single feature training data"
        assert self.a_ is not None and self.b_ is not None, \
            "must fit before predict!"

        return np.array([self._predict(x) for x in x_predict])

    def _predict(self, x_single):
        """给定单个待预测数据x_single， 返回x_single的预测结果值"""
        return self.a_ * x_single + self.b_

    def __repr__(self):
        return "SimpleLinearRegression2()"

可以看到除了fit方法中代码改变其他都代码都没变化。下面我们来测试一下两种模型的效率：

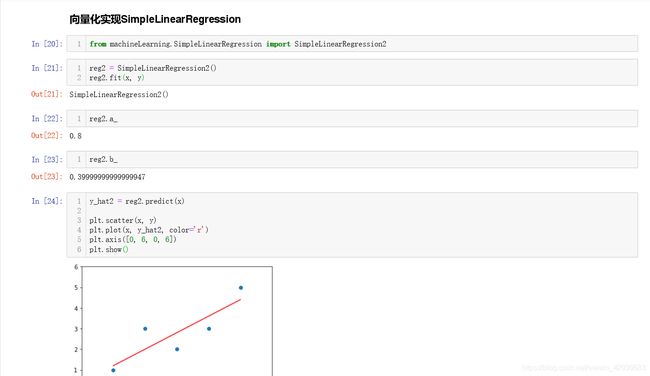
这里我们的向量化后的模型生成的数据与之前的模型参数都是没有差别的，下面我们来测试两种fit方法的效率，我们创建一个百万级数据去测试时间：

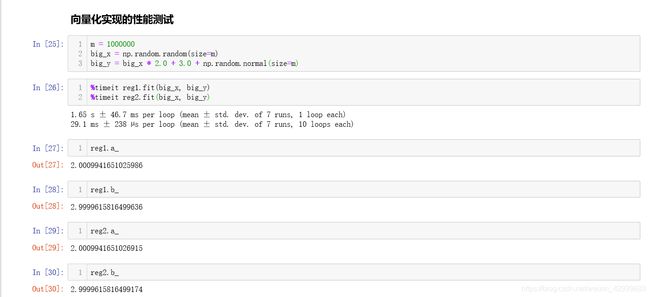
可见向量化后的模型比使用for循环的模型要快了50倍，这也是python中使用numpy的高效性，表示以后的python编程如果可以使用向量化实现会大大提高代码的效率。

回归算法的评价

实际上我们上面的例子的目标都是找到a和b，使得下面这个式子尽可能的小：$$\sum _{i=1}^m(y_{train}^{(i)}-a{x}_{train}^{(i)}-b{)}^2$$但是在实际对于模型的好坏的评价时是基于在测试数据集上所表现出来的性能，模型好坏的衡量标准是与${\sum }_{i=1}^m(y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}{)}^2$有关，这里就引出了一个问题，如果你的模型损失函数的结果值是1000，我的模型损失函数的结果值是800，那么是否我的模型就要比你的模型出色呢？答案肯定不是这样的，如果你的数据有10000个得到的损失是1000，而我的数据仅仅有10个得到的损失是800，显然是你的模型更加优秀，可见损失函数是与m的值有关的。

于是我们引出了三种衡量误差的方法：
1.均方误差MSE（Mean Squared Error）$\frac{1}{m}{\sum }_{i=1}^m(y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}{)}^2$
2.均方根误差RMSE（Root Mean Squared Error）$\frac{1}{m}\sqrt{{\sum }_{i=1}^m(y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}{)}^2}$
3.平均绝对误差MAE（Mean Absolute Error）$\frac{1}{m}{\sum }_{i=1}^m|y_{test}^{(i)}-{\hat{y}}_{test}^{(i)}|$

下面让我们编程看一下三种误差，这里我们使用sklearn中的波士顿房产数据：

由于可视化需求并且我们运用简单回归这我们只取一个特征：

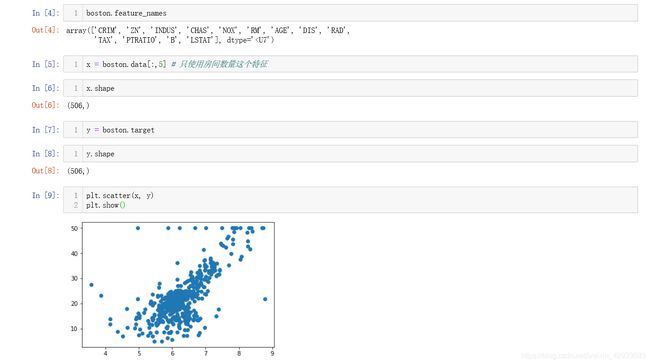
数据中价格在50处出现了很多分布特殊的点，造成这种情况的原因有很多，比如表格房产本身价值超出了50万元，所以我们这里把50万元及50万元以上的样本点都去掉：

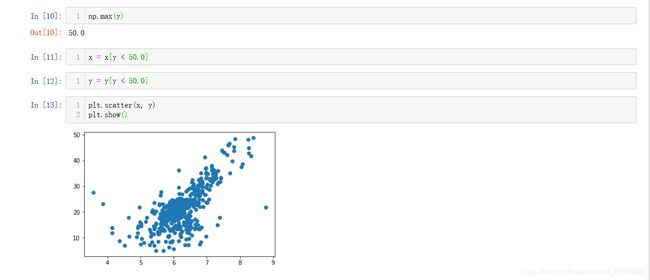
分割好之后创建训练和测试数据集：

这里用到的train_test_split在sklearn中也有，可以自己封装一个：

import numpy as np

def train_test_split(X, y, test_ratio=0.2, seed=None):
    """将数据 X 和 y 按照test_ratio分割成 X_train, X_test, y_train, y_test"""

    assert X.shape[0] == y.shape[0], \
        "the size of X must be equal to the size of y"
    assert 0.0 <= test_ratio <= 1.0, \
        "test_ration must be valid"

    if seed:
        np.random.seed(seed)

    shuffled_indexes = np.random.permutation(len(X))

    test_size = int(len(X) * test_ratio)
    test_indexes = shuffled_indexes[:test_size]
    train_indexes = shuffled_indexes[test_size:]

    X_train = X[train_indexes]
    y_train = y[train_indexes]

    X_test = X[test_indexes]
    y_test = y[test_indexes]

    return X_train, X_test, y_train, y_test

下面使用三种误差评估去评价模型：

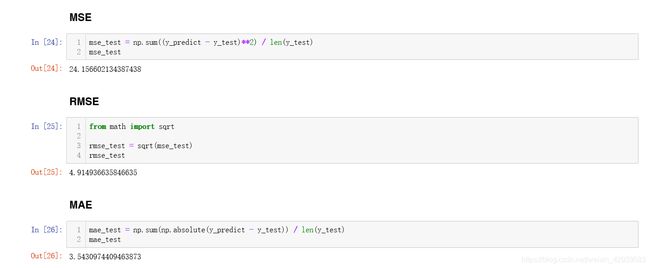
这里就可以看出均方误差实际上有着量纲的问题，实质上是x对y²的对应，采用均方根误差就可以看出模型的误差大概在5万元左右，平均绝对误差显示模型误差大概在3.5万元左右，但这都不是最好评价回归模型的指标，对于回归问题来说：对于不同的样本模型有着不同的RMSE和MAE，如何比较就有了局限性，从而引出了最好的衡量线性回归法的指标，也是scikit-learn中线性回归法评价的指标：

R Squared
$$R^2=1-\frac{S{S}_{residual}}{S{S}_{total}}=1-\frac{{\sum }_i^m({\hat{y}}^{(i)}-y^{(i)}{)}^2}{{\sum }_i^m(\overline{y}-y^{(i)}{)}^2}$$上面式子中$S{S}_{residual}$为Residual Sum of Squares，$S{S}_{total}$为Total Sum of Squares。这个式子看着复杂实质上并不复杂，对于式中分子的式子是使用我们的模型预测产生的错误，分母就比较有意思了，是使用$\overline{y}=y$预测产生的错误，也就是说明我们不需要任何预测，仅仅用均值去预测所有值，在统计学上这种模型被称为Baseline Model，可以理解为最差的基准线模型，R²指标衡量了我们模型没有产生错误部分（拟合部分）的大小，并且我们还可以得到以下几个性质：

1）$R^2\le 1$
2）$R^2$越大越好，当我们的模型不犯任何错误时，$R^2$得到最大值。
3）当我们的模型等于基准模型时，$R^2$为0。
4）如果$R^2<0$，说明我们学习到的模型还不如基准模型，此时，很有可能我们的数据不存在任何线性关系，需要重新考虑。

同时在计算$R^2$时还可以作变换：$$R^2=1-\frac{{\sum }_i^m({\hat{y}}^{(i)}-y^{(i)}{)}^2}{{\sum }_i^m(\overline{y}-y^{(i)}{)}^2}=1-\frac{{\sum }_i^m({\hat{y}}^{(i)}-y^{(i)}{)}^2/m}{{\sum }_i^m(\overline{y}-y^{(i)}{)}^2/m}=1-\frac{MSE(\hat{y},y)}{Var(y)}$$于是我们可以实现自己的R Squared：

def r2_score(y_true, y_predict):
    """计算y_true和y_predict之间的R Square"""

    return 1 - mean_squared_error(y_true, y_predict) / np.var(y_true)

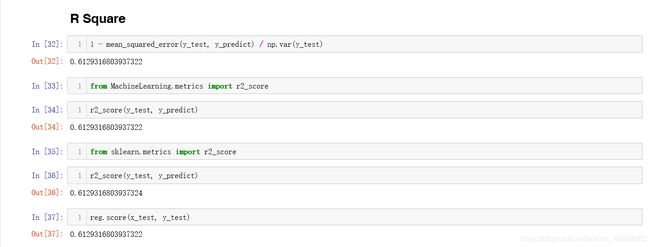
使用R Squared可以给回归模型打分，也就是sklearn中封装好的score函数。

4 多元线性回归和正规方程解

在实际的应用场景之中我们的样本特征肯定不止一个，可能会有多个甚至无穷个，这样简单线性回归就无法满足我们的需求，就必须从一元线性回归拓展到多元线性回归，但是多元线性回归的求解思路与简单线性回归是一致的。

我们的样本变为$$x^{(i)}=(X_1^{(i)},X_2^{(i)},...,X_n^{(i)})$$一个样本包含多个样本特征，使$x^{(i)}$变为了一个向量，同样样本预测值变为$$\hat{y}={\theta }_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+...+{\theta }_n{X}_n^{(i)}$$我们的目标仍然是使下式尽可能的小：$$\sum _{i=1}^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$目标就是找到最小值时的${\theta }_0,{\theta }_1,...,{\theta }_n$。这里对于预测值做一个小小的修改：$$\hat{y}={\theta }_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+...+{\theta }_n{X}_n^{(i)}$$其中$$\theta =({\theta }_0,{\theta }_1,{\theta }_2,...,{\theta }_n{)}^T$$把这个式子写成一种更简洁的形式：$$\hat{y}={\theta }_0{X}_0^{(i)}+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+...+{\theta }_n{X}_n^{(i)},X_0^{(i)}\equiv 0$$$$x^{(i)}=(X_0^{(i)},X_1^{(i)},X_2^{(i)},...,X_n^{(i)})$$$${\hat{y}}^{(i)}=X^{(i)}\cdot \theta$$这样就像我们之前提到的向量化运算一样可以大大加快运算速度。为了实现上面的思路我们一般要对样本特征矩阵作修改，修改后的矩阵如下：$$X_b=\left[\begin{array}{ccccc}1& X_1^{(1)}& X_2^{(1)}& ...& X_n^{(1)}\\ 1& X_1^{(2)}& X_2^{(2)}& ...& X_n^{(2)}\\ ...& ...& ...& & ...\\ 1& X_1^{(m)}& X_2^{(m)}& ...& X_n^{(m)}\end{array}\right]\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\\ ...\\ {\theta }_n\end{array}\right]$$在参数$\theta$中${\theta }_0$是截距intercept，${\theta }_1...{\theta }_n$是系数coefficients。这样变换以后，我们的损失函数也可以变换为向量化表示的形式，我们的目标就是使下式尽可能的小：$$(y-X_b\cdot \theta {)}^T(y-X_b\cdot \theta )$$最优化上面这个损失函数的解法这里就不介绍了，因为我自己在看多元线性回归的解法时也是云里雾里，至于解法就留给数学家去解决吧，感兴趣的同学可以搜索一下，网上有很多关于多元线性回归的解法文章，这里我们需要知道的是，上面这个方程确确实实是有解的，解就是下面这个式子：$$\theta =(X_b^T{X}_b{)}^{-1}{X}_b^{T}y$$这个式子就被称为多元线性回归的正规方程解(Normal Equation)，也就是说我们在编程时直接运算出该结果就可以得到最好的模型，但遗憾的是正规方程解在运算时时间复杂度很高，达到了$O(n^3)$的级别，就算优化过也只能得到$O(n^{2.4})$，但是优点在于不需要对数据进行归一化处理，但实际情况中我们在求解多元线性回归时并不使用这种方法，而是使用我们下一小节介绍的梯度下降法，原因会在下一小节说明，但是同学们要知道其实多元线性回归是有一个简洁的式子可以直接求得正规方程解的，现在我们可以使用正规方程解去创建我们自己的多元线性回归类：

import numpy as np
from .metrics import r2_score

class LinearRegression:

    def __init__(self):
        """ 初始化Linear Regression模型"""
        self.coef_ = None
        self.interception_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train,y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.interception_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)


    def __repr__(self):
        return "LinearRegression("

我们再使用我们的多元线性回归模型去预测上一小节完整的波士顿房产模型，同时拿我们的模型与sklearn中的线性回归模型作比较：



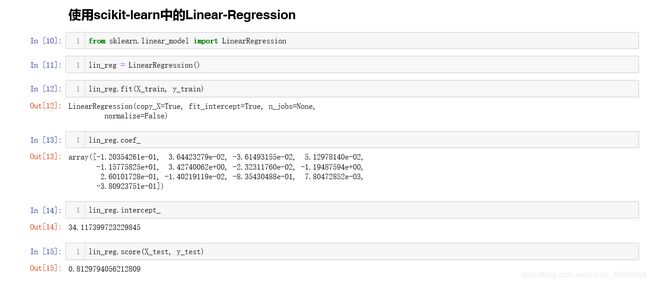
从结果可以看出来我们的模型在结果上是与sklearn中封装的线性回归模型的差别几乎是没有的，但时间却慢了很多，我这里没有截取运行时间的图片，实质上sklearn中的线性回归在搜索最优参数时是采用的梯度下降法，那么就让我们来一起学习一下梯度下降法吧！

5 梯度下降法

在开头我们说过，梯度下降法本身并不是一个机器学习算法，而是一种基于搜索的最优化方法，它的作用就是最小化一个损失函数，相对就有梯度上升法，可以用来最大化一个效用函数。

在二维平面上，导数可以代表方向（手画的图凑合看哈）：

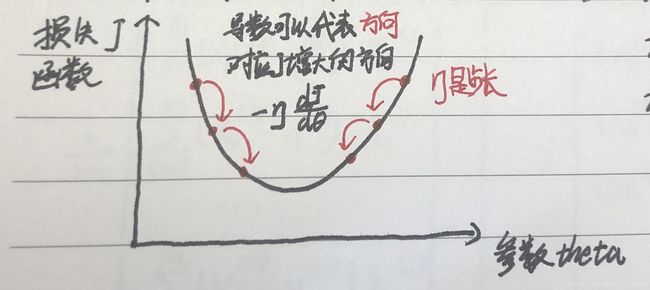
在二维平面中导数代表增大的方向，但我们寻找的是极小值，故我们要用斜率去乘以$-\eta$，这里的$\eta$称为学习率，$\eta$的取值影响获得最优解的速度，如果取值$\eta$太小了程序需要多次迭代直到走到极小值，$\eta$的取值不合适，甚至得不到最优解，如果$\eta$取值太大了就会在极小值旁来回跳跃，$\eta$是梯度下降法的一个超参数。如果你看不懂上面这个图，简单来说，梯度下降法就是，损失函数J在多维空间中就是一个“山谷”，我们在损失函数上放置一个“球”，球会沿着梯度负方向滚落，滚落到最低点可以找到一个$\theta$，但是球的滚落速度由$\eta$决定。 通过这段话再去结合上图理解，在多维空间中，梯度代表了J增大的方向：

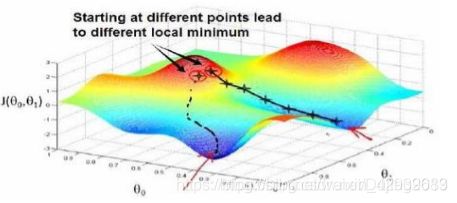
但是并不是所有函数都有唯一的极值点，如上图中就有两个极小值点，搜索策略可能找到的是局部最优解，但不是全局最优解，所有有时我们需要多次运行并且随机化初始点，同时梯度下降法的初始点也是一个超参数。但在线性回归中只有一个极小值点，这也是上一小节最后两种策略结果一致的原因。

下面模拟一下梯度下降法，使用简单的二次曲线：

封装计算导数与函数的两个函数并且在这里使用梯度下降时不要使用双等号，计算机在计算浮点数时会有不精确数，这里我们规定梯度减小的幅度足够小是我们就停止迭代：

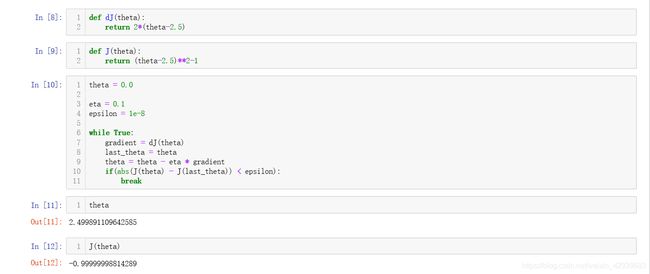
我们创建一个列表去保存一下每一次下降后$\theta$所处于的位置，最后将整个$\theta$下降的过程可视化出来，我们可以看到我们以$\eta$=0.1时，到最后找到最小的值下降了46次：

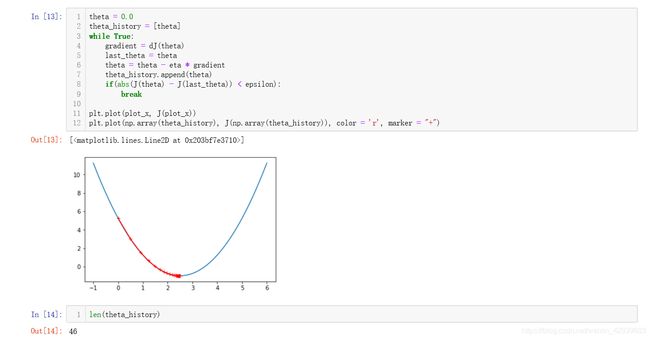
把梯度下降函数与绘图函数封装起来：

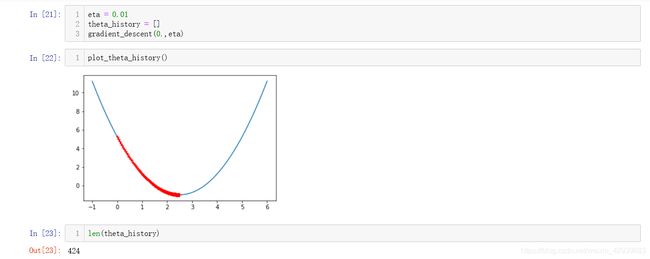
我们将$\eta$变为0.01减小10倍，可以看到之前描述的第一种情况，迭代了424次才达到最小值：

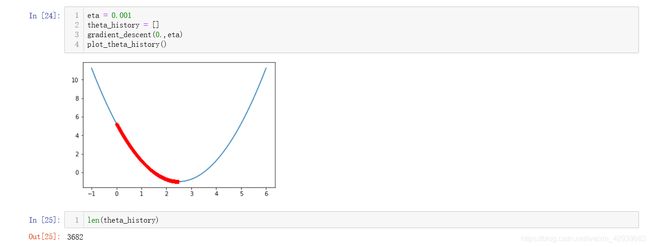
如果将$\eta$再缩小10倍，那迭代次数也会随着量级上升，达到3600次左右：

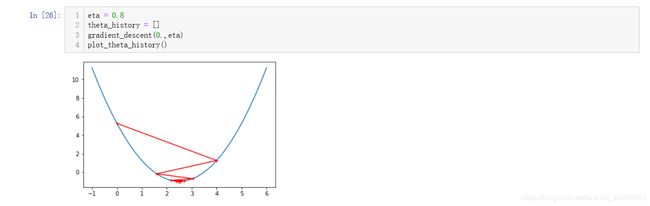
将$\eta$缩小虽然会导致算法搜索缓慢，还是可以找到正确的结果，但如果将$\eta$变大，则会出现跳跃的情况，这里$\eta$为0.8出现了在函数两边来回跳跃，但最后还是能下降到一个比较好的值：

当$\eta$一旦超过了某个阈值，无论进行多少次迭代都无法寻找到最好的值，下面我修改一下代码防止溢出来展示一下效果：

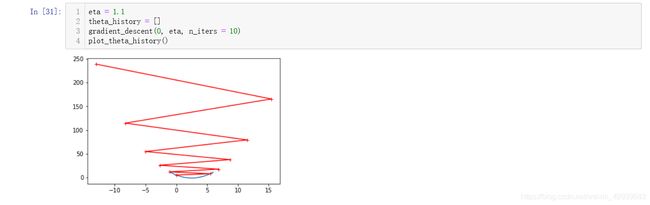
注意这里第一个起始点是在0点的，也就是最下面的点，这说明寻找过程是不断增大的，永远找不到最佳的位置最后导致浮点溢出。所以学习率$\eta$作为超参数在模型建立之前也是要谨慎选好的，否则会在不同的程度上影响算法的效率。

6 线性回归中的梯度下降法

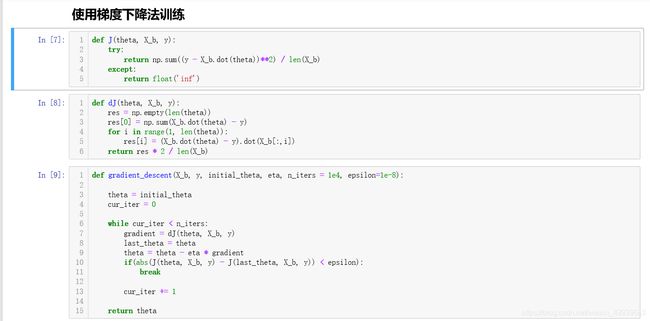
了解了梯度下降法以后，让我们来把梯度下降法作用到线性回归的例子中，以上一节中的二次曲线为例，有了代价函数，去找梯度，从之前我们分析多元线性回归模型可以得到我们的目标，这里我们选取之前我们考虑过的MSE来作为损失函数：$$\frac{1}{m}\sum _i^m(y^{(i)}-{\hat{y}}^{(i)}{)}^2$$我们的目标也就是使上式尽可能的小，其中$$\hat{y}={\theta }_0+{\theta }_1{X}_1^{(i)}+{\theta }_2{X}_2^{(i)}+...+{\theta }_n{X}_n^{(i)}$$也就可以把目标变为使下式尽可能的小$$\frac{1}{m}\sum _i^m(y^{(i)}-{\theta }_0-{\theta }_1{X}_1^{(i)}-{\theta }_2{X}_2^{(i)}-...-{\theta }_n{X}_n^{(i)}{)}^2$$下面我们就开始对损失函数求偏导得到梯度了$$▽J(\theta )=\left(\begin{array}{c}\partial J/\partial {\theta }_0\\ \partial J/\partial {\theta }_1\\ ...\\ \partial J/\partial {\theta }_n\end{array}\right)=\frac{1}{m}\left(\begin{array}{c}{\sum }_i^{m}2(y^{(i)}-X_b^{(i)}\theta )(-1)\\ {\sum }_i^{m}2(y^{(i)}-X_b^{(i)}\theta )(-X_1^{(i)})\\ .....\\ {\sum }_i^{m}2(y^{(i)}-X_b^{(i)}\theta )(-X_n^{(i)})\end{array}\right)$$$$=\frac{2}{m}\left(\begin{array}{c}{\sum }_i^m(X_b^{(i)}\theta -y^{(i)})\\ {\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_1^{(i)}\\ ....\\ {\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_n^{(i)}\end{array}\right)$$到这里就得到了我们损失函数的梯度了。让我们编程实现一下：
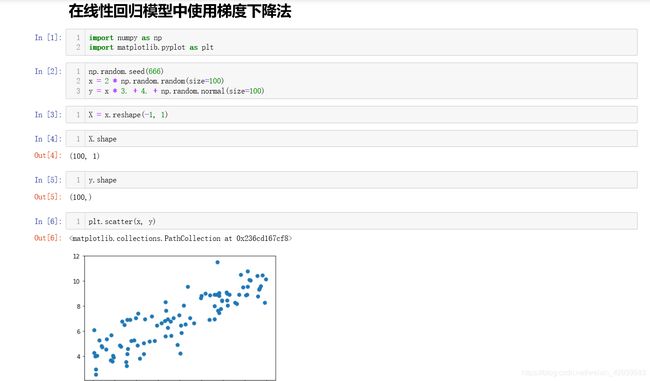
这里为了可视化便于理解我使用的还是二维数据，但你可以看到数据是以矩阵形式存储，也就是100行1列的数据，这样无论几元传入只要是矩阵即可：

按照上面的逻辑和结果我们去封装自己的梯度下降法：


结果的展示与我们上面提到的是一样的，数组第一个元素是截距，后面的为系数，现在我们的算法已经可以得到正确的结果了，但是我们想要更快，就要把计算方法向量化。

线性回归梯度下降的向量化

从上面的结果开始继续往下推导我们可以得到：$$J(\theta )=\frac{2}{m}\left(\begin{array}{c}{\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_0^{(i)}\\ {\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_1^{(i)}\\ ....\\ {\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_n^{(i)}\end{array}\right)=$$$$\frac{2}{m}(X_b^{(1)}\theta -y^{(1)},X_b^{(2)}\theta -y^{(2)},...,X_b^{(m)}\theta -y^{(m)})$$$$\cdot \left(\begin{array}{ccccc}{X}_0^{(1)}& X_1^{(1)}& X_2^{(1)}& ...& X_n^{(1)}\\ X_0^{(2)}& X_1^{(2)}& X_2^{(2)}& ...& X_n^{(2)}\\ X_0^{(3)}& X_1^{(3)}& X_2^{(3)}& ...& X_n^{(3)}\\ ...& ...& ...& ...& ...\\ X_0^{(m)}& X_1^{(m)}& X_2^{(m)}& ...& X_n^{(m)}\end{array}\right)$$ $$=\frac{2}{m}\cdot (X_b\theta -y{)}^T\cdot X_b$$这样我们就得到了一个十分简洁的式子，同时运算效率也会大大提升，让我们自己封装我们的多元线性回归类吧，其中我把非向量化的过程注释了：

import numpy as np
from .metrics import r2_score


class LinearRegression:

    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.interception_ = None
        self._theta = None

    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train,使用正规方程法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        X_b = np.hstack([np.ones((len(X_train), 1)),X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def fit_bgd(self, X_train, y_train, eta=0.01, n_iters=1e4):
        """根据训练数据集 X_train, y_train,使用批量梯度下降法训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            try:
                return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
            except:
                return float('inf')

        def dJ(theta, X_b, y):
            """非向量化计算梯度"""
            # res = np.empty(len(theta))
            # res[0] = np.sum(X_b.dot(theta) - y)
            # for i in range(1, len(theta)):
            #     res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            # return res * 2 / len(X_b)
            """向量化计算梯度"""
            return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

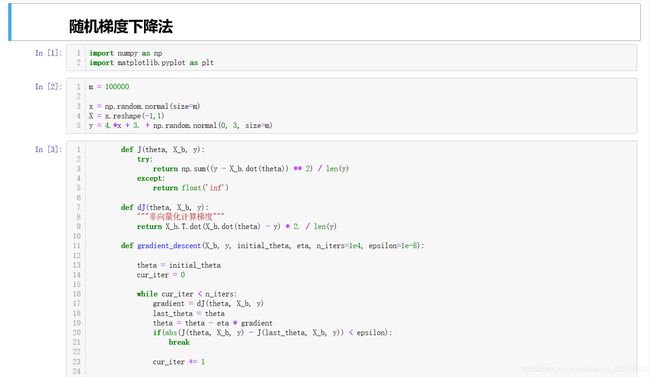
        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

            theta = initial_theta
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break

                cur_iter += 1

            return theta

        X_b = np.hstack([np.ones((len(X_train),1)), X_train])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    
    def predict(self, X_predict):
        """给定待预测数据集X_predict, 返回表示X_predict的结果向量"""
        assert self.interception_ is not None and self.coef_ is not None,\
            "must fit before predict"
        assert X_predict.shape[1] == len(self.coef_),\
            "the feature number of X_predict must be equal to X_train"

        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)

    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""

        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)

    def __repr__(self):
        return "LinearRegression()"

现在让我们用真实的数据波士顿房产模型去测试一下我们的模型：



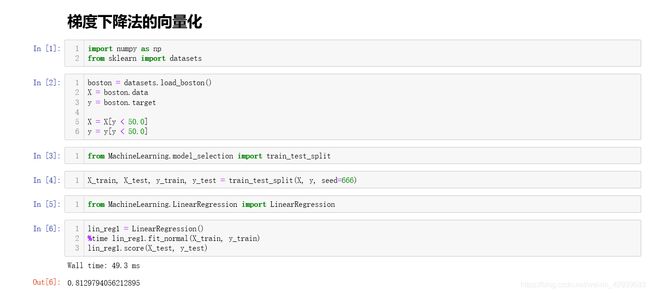
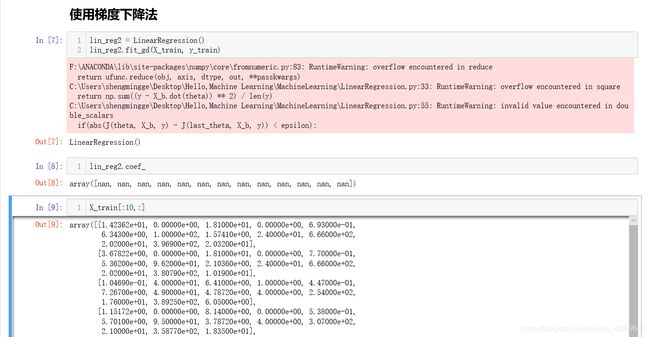
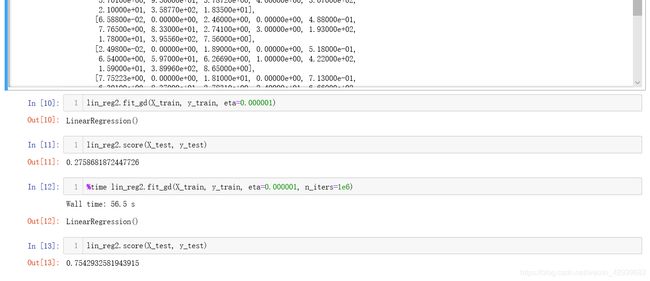
从上面的结果显示来看，我们在传入训练数据集是模型python为我们提示了警告，同时查看模型的系数后发现所有的系数都是none，我们在去观察训练数据集的前十个特征发现，其中有的特征量级达到了100，有的数据量级只有0.1，这就导致梯度下降过程中迭代次数的增加，当默认次数学习完成以后我们的R Squared平均仅仅只有0.27分，再手动增加迭代次数到百万级以后，花费了将近一分钟的时间才把模型分数提高到了0.75，而我们上一节正规方程解仅仅使用50ms就可以达到0.8分，这难道是梯度下降法出了问题么？

数据归一化（Feature Scaling）

在我们的算法模型中，如果遇到了样本的特征的变化量远远大于其他的变换量，那么预测结果就会被这个特征所主导，因此我们需要将所有的数据映射到同一个尺度。

均值方差归一化（standardization）：把所有数据归一到均值为0方差为1的分布中$$x_{scale}=\frac{x-x_{mean}}{S}$$我们可以封装自己的归一化类：

import numpy as np

class StandardScaler:

    def __init__(self):
        self.mean_ = None
        self.scale_ = None

    def fit(self, X):
        """根据训练数据集X获得数据的均值和方差"""
        assert X.ndim == 2, "The dimension of X must be 2"

        self.mean_ = np.array([np.mean(X[:, i]) for i in range(X.shape[1])])
        self.scale_ = np.array([np.std(X[:, i]) for i in range(X.shape[1])])

        return self

    def transform(self, X):
        """将X根据这个StandardScaler进行均值方差归一化处理"""
        assert X.ndim == 2, "The dimension of X must be 2"
        assert self.mean_ is not None and self.scale_ is not None, \
        "must fit before transform!"
        assert X.shape[1] == len(self.mean_),\
        "the feature number of X must be equal to mean_ and std_"
        resX = np.empty(shape = X.shape, dtype = float)
        for col in range(X.shape(1)):
            resX[:,col] = (X[:,col] - self.mean_[col]) / self.scale_[col]

        return resX

下面我们来对归一化后的数据进行梯度下降法：

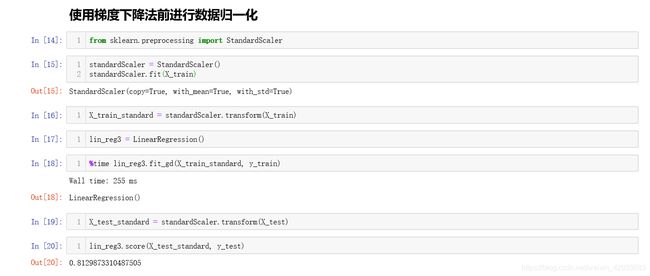
可以看到结果梯度下降法的速度提高了很多，但是为什么比起正规方程解来说还是慢了呢？实质上是因为数据流太小了，我们创建一个较大的数据再来比较：

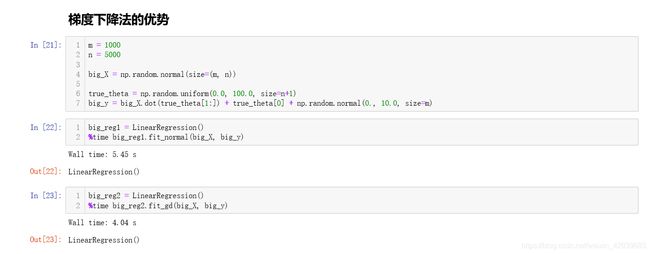
这里仅仅到几千个特征就可以体现出梯度下降法的优势了，而5000个特征还装不进一个100✖100像素的图像，如果数据再大更能体现出优势了。这里我创建的数据是样本特征数远大于样本数，这种情况下当计算梯度时每一个样本都参与进来计算梯度，效率会比较快，但在实际情况下我们的样本数目很有可能会远远大于样本特征数目，这样想让每一个样本都参与计算显然计算量是十分巨大的，由此我们引出了随机梯度下降法。

7 随机梯度下降法

我们已经实现的梯度下降法是批量梯度下降法（Batch Gradient Densent）。而随机梯度下降法（Stochastic Gradient Descent）就规避了样本数量m过大导致运算缓慢的影响。批量梯度下降法中的梯度为：$$\frac{2}{m}\left(\begin{array}{c}{\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_0^{(i)}\\ {\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_1^{(i)}\\ ....\\ {\sum }_i^m(X_b^{(i)}\theta -y^{(i)})X_n^{(i)}\end{array}\right)$$随机梯度下降法的思想就是在这一步把梯度的取值改变为：$$m\left(\begin{array}{c}(X_b^{(i)}\theta -y^{(i)})X_0^{(i)}\\ (X_b^{(i)}\theta -y^{(i)})X_1^{(i)}\\ ....\\ (X_b^{(i)}\theta -y^{(i)})X_n^{(i)}\end{array}\right)=2\cdot (X_b^{(i)}{)}^T\cdot (X_b^{(i)}\theta -y^{(i)})$$这时上式已经不是梯度了，而是我们随机取出一个i去求上式，它也是一个方向，虽然不是下降最快的方向但是也在下降（大部分情况）。上图（很丑）！

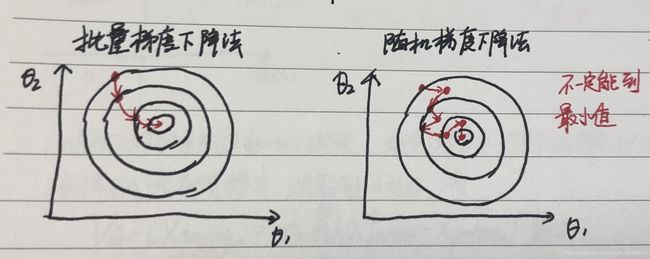
就想上图中画的一样，随机梯度下降法不一定可以取到最小值，但是用精度换取了时间，t同时我们要让（步长）学习率$\eta$逐渐减小，因为最后搜索到最后如果$\eta$是不变的很有可能会离开最小值区域，那么我们就把学习率规定为下式：$$\eta =\frac{t_0}{i\_iters+t_1}$$其中t0和t1都是超参数，学习率会随着循环次数i_iters的增加而减小，t1是缓解初始时学习率变换过大而设立。让我们来看一下随机梯度下降法的作用：


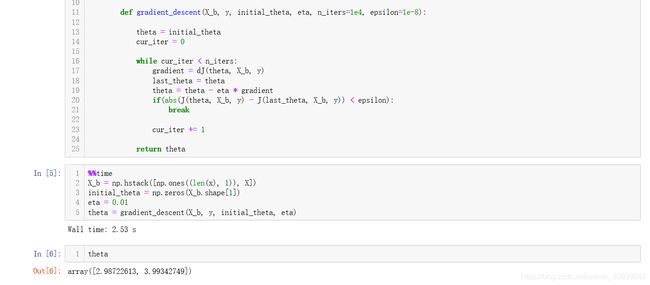
这里我们把样本数目设置很大，使用我们的批量梯度下降法最后运行时间在2.5秒左右。

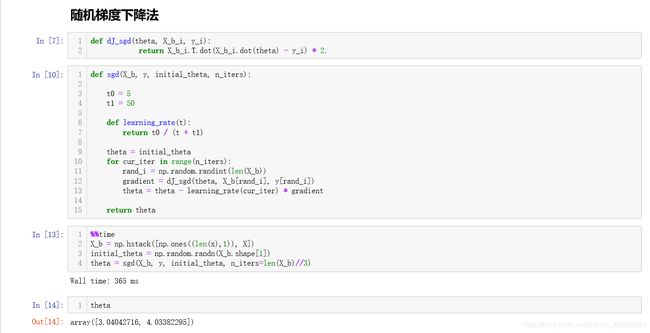
按照我们上面的逻辑实现随机梯度下降法，可以看到最后仅仅用了365毫秒就得到了一个不错的结果，虽然有偏差，但也是我们可以接受的，这样我们就可以在自己的多元线性回归模型中分装自己的随机梯度下降法：

    def fit_sgd(self, X_train, y_train, n_iters=50, t0=5, t1=50):
        """根据训练数据集 X_train, y_train,使用随机梯度下降法训练LinearRegression模型"""
        assert X_train.shape[0] == y_train.shape[0],\
            "the size of X_train must be equal to the size of y_train"
        assert n_iters >= 1,\
            "the iterations must greater than 0"

        def dJ_sdg(theta, X_b_i, y_i):
            return X_b_i * (X_b_i.dot(theta) - y_i) * 2.

        def sgd(X_b, y, initial_theta, n_iters=5, t0=5, t1=50):

            def learning_rate(t):
                return t0 / (t + t1)

            theta = initial_theta
            m = len(X_b)
            for i_iter in range(n_iters):
                """我们在这里为了可以随机的遍历到所有的样本点，使用双重循环去限制取出每个样本的次数
                    每次循环都将整个样本的索引打乱，去随机取出整个样本空间"""
                indexes = np.random.permutation(m)
                X_b_new = X_b[indexes,:]
                y_new = y[indexes]
                for i in range(m):
                    gradient = dJ_sdg(theta, X_b_new[i], y_new[i])
                    """这里的学习率就要是外循环次数乘以样本个数在加上当前内循环遍历进行到的次数"""
                    theta = theta - learning_rate(i_iter * m + i) * gradient

            return theta
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta = np.random.randn(X_b.shape[1])
        self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)

        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

这里代码实现的随机并不是真正的随机，我们使用打乱索引去实现假随机，这样的好处是所有的样本点我们都可以用到，并且在使用模型时我们仅仅使用样本数目的三分之一次循环就可以得到一个较好的结果。

8 小结

实质上我们实现的批量梯度下降法与随机梯度下降法比sklearn中的梯度下降法效率还是低很多的，sklearn中的梯度下降法封装了更复杂的算法，这里仅仅是希望大家可以理解整个梯度下降法的过程就可以了。并且整篇文章仅仅只是讲述了线性回归和梯度下降法的皮毛，比如梯度的调试，使用更快的式子代表梯度，小批量梯度下降法都没有讲到，还有更深更广的知识等待大家去学习，希望大家可以坚持继续学习，大家加油！