综述：机器学习在CTR中的应用

背景：设计个性化信息检索时，用户行为预测扮演着重要的作用。用户行为预测的目标是估计用户点击、购买等行为的概率，而该概率代表了用户对该item的兴趣程度，用户之前的行为同时也影响着我们随后的排序。如何根据用户的query选择正确的ads并对其进行合理的排序，不仅极大的影响着用户点击、浏览等行为，而且对于搜索广告的收益也起到重要的作用。
IR任务中，数据大部分为multi-field类型，例如：[weekday=Tuesday, Gender=Male, City=London]，我们可以通过one-hot对其进行编码，映射为高维稀疏特征。例如，我们可以将上述特征进行one-hot编码，然后concatenate得到

LR

，其中为特征，为特征权重，b为偏差。

Degree-2 Polynomial (Poly2)

简介： LR模型具有计算高效、可解释性强等优点，但是需要人工抽取交叉特征。而交叉特征对于模型性能起到重要的作用，相比LR线性模型，Poly2设计了特征自动交叉，从而自动计算交叉特征提升模型性能。

是将，编码为一个自然数的函数。

FM

简介： Poly2模型虽然能够自动抽取交叉特征，但是当特征维度较高并且稀疏时，权重难以收敛。针对该问题作者提出了FM算法，其中正定矩阵，可以通过特征向量空间渐进表示。
${\mathop{\rm y}\nolimits} \left( {\bf{x}} \right): = {w_0} + \sum\limits_{i = 1}^n {{x_i}{w_i} + \sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n { < {{\bf{v}}_i},{{\bf{v}}_j} > {x_i}{x_j}} } }$
$\begin{array}{l} \sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n { < {{\bf{v}}_i},{{\bf{v}}_j} > {x_i}{x_j}} } \\ = \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n { < {{\bf{v}}_i},{{\bf{v}}_j} > {x_i}{x_j}} } - \frac{1}{2}\sum\limits_{i = 1}^n { < {{\bf{v}}_i},{{\bf{v}}_i} > {x_i}{x_i}} \\ = \frac{1}{2}\left( {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\sum\limits_{f = 1}^k {{v_{i,f}}{v_{j,f}}} {x_i}{x_j}} } - \sum\limits_{i = 1}^n {\sum\limits_{f = 1}^k {{v_{i,f}}{v_{i,f}}{x_i}{x_i}} } } \right)\\ = \frac{1}{2}\sum\limits_{f = 1}^k {\left( {\left( {\sum\limits_{i = 1}^n {{v_{i,f}}} {x_i}} \right)\left( {\sum\limits_{j = 1}^n {{v_{j,f}}} {x_j}} \right) - \sum\limits_{i = 1}^n {v_{i,f}^2x_i^2} } \right)} \\ = \frac{1}{2}\sum\limits_{f = 1}^k {\left( {{{\left( {\sum\limits_{i = 1}^n {{v_{i,f}}} {x_i}} \right)}^2} - \sum\limits_{i = 1}^n {v_{i,f}^2x_i^2} } \right)} \end{array}$
是一个无对角线的上三角矩阵，直接可以计算整个矩阵然后减去对角线。

FFM

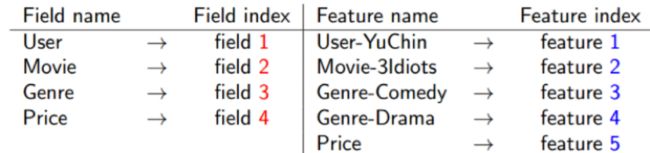
简介： FM算法将所有特征归结到一个field，而FFM算法则按照field对不同特征进行区分，主要体现在交叉项中。在FM算法中user这个特征对应的latent vector不论是对price、genre还是movie都是相同的，而FFM算法中则对特征进行归类，latent vector会区分交叉filed，模型参数个数n(n-1)/2。可以看出来FM算法时FFM算法的一个特例，但是随着FFM算法对latent vector的细化，FM算法中交叉简化将不再适用.

y\left( x \right) = {w_0} + \sum\limits_{i = 1}^n {{x_i}{w_i}} + \sum\limits_{{j_1} = 1}^n {\sum\limits_{{j_2} = {j_1} + 1}^n {\left( {{{\bf{w}}_{{j_1},{f_2}}} \cdot {{\bf{w}}_{{j_2},{f_1}}}} \right)} } {x_{{j_1}}}{x_{{j_2}}}

其中，，分别表示，对应的field，代表与交叉的权重。

FwFMs

简介： FFM算法按照field对latent vector进行区分，从而提升模型的效果。但是FFM算法没有区分不同特征交叉的重要性，本文针对不同特征交叉赋予不同的权重，从而达到更精细的计算交叉特征的目的。
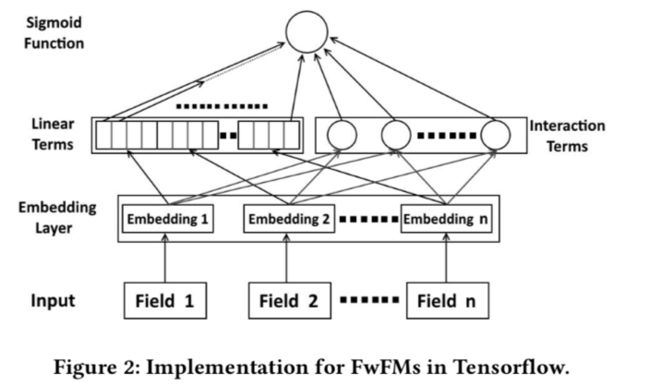
网络结构

{\mathop{\rm y}\nolimits} \left( {\bf{x}} \right): = {w_0} + \sum\limits_{i = 1}^n {{x_i}{w_i} + \sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n { < {{\bf{v}}_i},{{\bf{v}}_j} > {x_i}{x_j}} } } {r_{{\mathop{\rm F}\nolimits} (i),{\mathop{\rm F}\nolimits} (j)}}

其中，表示field ，交叉特征的重要性。

AFM

简介： AFM算法与FwFM算法类似，目标都是希望通过对不同交叉特征采用不同权重，从而减少引入噪声提升模型性能。

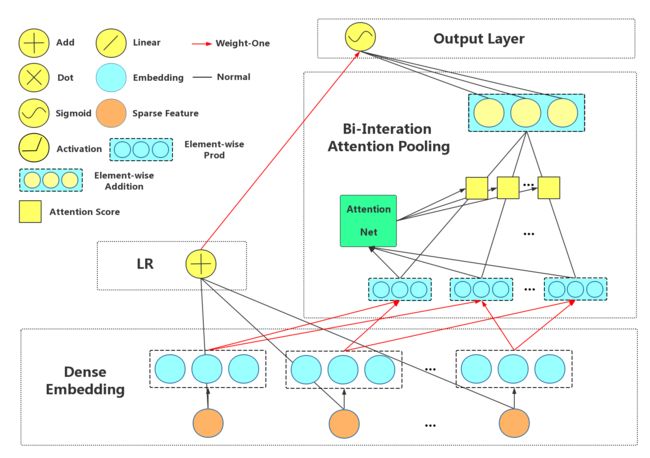
AFM的embedding层后，先让个field的特征做了element-wise product后，得到个交叉项，然后AFM引入了一个Attention Net，认为这些交叉特征项每个对结果的贡献是不同的。例如和的权重重要度，用来表示。从这个角度来看，其实AFM其实就是个加权累加的过程。
1: Attention-based Pooling Layer

2:AFM模型结构
$y\left( x \right) = {w_0} + \sum\limits_{i = 1}^n {{x_i}{w_i}} + {{\bf{p}}^{\rm{T}}}\sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {{a_{ij}}\left( {{{\bf{v}}_i} \odot {{\bf{v}}_j}} \right)} } {x_i}{x_j}$

其中，，，，为模型参数。

FNN

简介： LR、FM被广泛的应用在工业场景中，但是这些模型对于抽取高阶特征显得无能为力。深度模型可以学习高阶复杂的交叉特征，对于提升模型性能有着重要的作用。由于CTR中大部分特征是离散、高维且稀疏的，需要embedding后才能用nn学习。

FNN模型将embedding层用FM初始化，即每个特征对应一个偏置项和一个k维向量。然后参数向量再随着训练不断学习调整。假设每个field的类别特征都只有一个1值，其余为0值，即可进行one-hot编码，然后做embedding，Dense Layer里每个Field对应的参数就是该Field那个不为0的变量对应的FM里的偏置项和k维隐向量。简单说模型第一层到第二层之间其实是普通的全连接层，而为0的输入变量对Dense Layer里的隐单元值不做贡献。
FNN模型结构

损失函数(最小交叉熵)为：

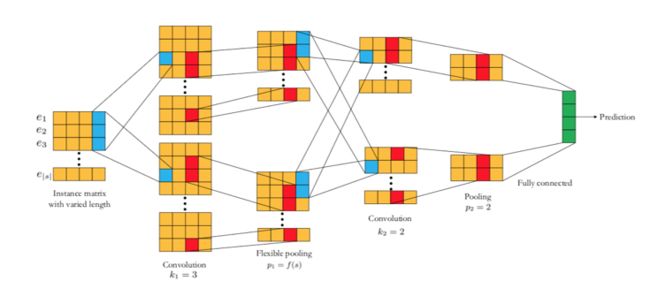
CCPM

简介： 模型结构整体结构相对比较简单，首先将特征映射到embedding稠密向量，然后经过卷积神经网络抽取高维特征，最后通过pooling层抽取主要的高维信息。

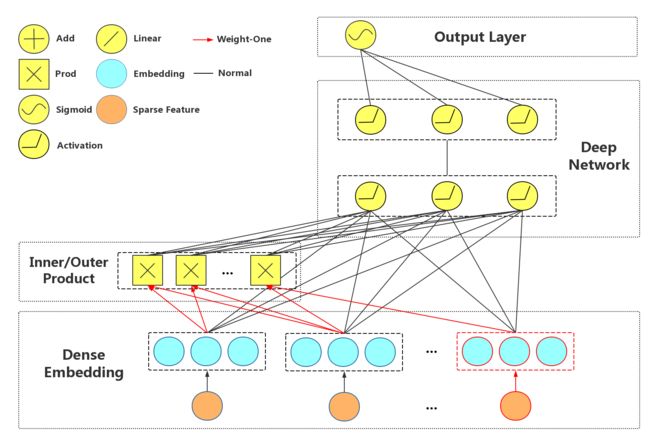
PNN

简介： FNN算法实际上是对特征embedding之后进行concatenate，再接FC，虽然使用了激活函数增加了非线性，实际上是对特征进行了加权组合(add 操作)。PNN算法与FNN算法的区别在于PNN算法中间多了一层Product Layer层。其中z为embedding层的线性部分，p为embedding层的特征交叉部分,其他与FNN算法结构相同。
网络结构

Product layer分为两部分，其中z代表线性信号向量，而p代表二次信号向量。
1: Inner Product-based Neural Network

，即用内积来表示特征的交叉，类似于“且”的关系，为embedding向量。
2: Outer Product-based Neural Network
，即用矩阵乘法来表示特征的交叉，类似于“和”的关系

Wide & Deep

简介： 线性模型具有计算高效、可解释性强等优点，但是模型的泛化性差。深度学习模型对于长尾特征具有更高的泛化性，并且不需要大量的特征工程。然而当交叉特征稀疏时，深度学习模型容易出现over-generalize。本文提出同时对线性模型和深度模型联合训练，从而结合线性模型记忆性强、深度模型泛化性强的优点。
网络结构
1: The Wide Component

wide部分长处在于学习样本中的高频部分，优点是模型的记忆性好，对于样本中出现过的高频低阶特征能够用少量参数学习；缺点是模型的泛化能力差，例如对于没有见过的ID类特征，模型学习能力较差
2: The Deep Component

其中，代表第层，为激活函数。
deep部分长处在于学习样本中的长尾部分，优点是泛化能力强，对于少量出现过的样本甚至没有出现过的样本都能做出预测（非零的embedding向量）;缺点是模型对于低阶特征的学习需要用较多参才能等同wide部分效果，而且泛化能力强某种程度上也可能导致过拟合出现badcase
3: Joint Training of Wide & Deep Model
${\bf{P}}\left( {{\rm{Y}} = 1|{\bf{x}}} \right) = \sigma \left( {{\bf{w}}_{wide}^{\rm{T}}\left[ {{\bf{x}},\Phi \left( {\bf{x}} \right)} \right] + {\bf{w}}_{deep}^T{{\bf{a}}^{{l_f}}} + b} \right)$
其中，为wide部分的权重，为deep部分的权重，其中是指交叉特征。

DeepFM

简介： FM算法仍然属于wide&deep架构，不过在wide部分做了改进，采用FM替换linear layer，从而通过FM算法对交叉特征的计算能力提升模型的整体性能。其中inner product和deep network共享embedding feature，因此模型能同时从原始特征中学习低阶、高阶特征，并且不需要专业特征。
网络结构
1:FM component

2:Deep component

3:combination output layer

NFM

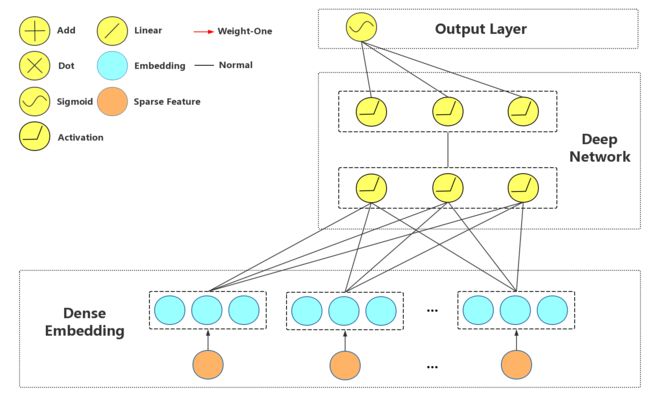
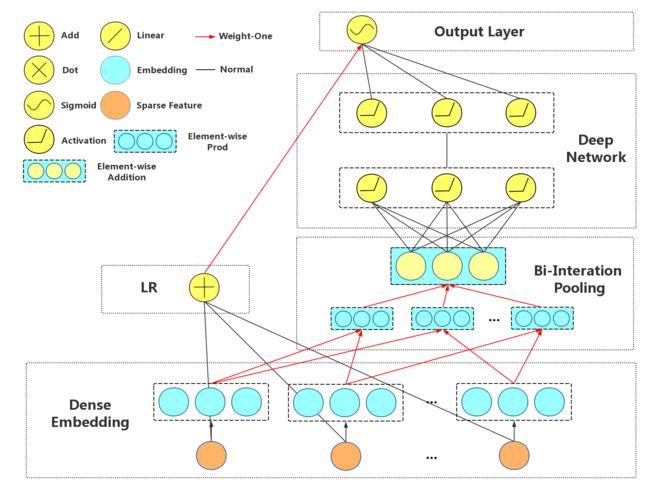
简介： FNN、wide&deep、DeepFM等算法在deep network部分都是对embedding之后的特征进行concatenate，未能充分进行特征交叉计算。本文NFM算法则是对embedding直接采用element-wise后sum起来做特征交叉，然后通过MLP直接将特征压缩，最后concatenate linear部分和deep部分的特征。
网络结构
1: Bi-Interaction Layer

{{\mathop{\rm f}\nolimits}_{BI}}\left( {{{\bf{v}}_x}} \right) = \frac{1}{2}\left[ {{{\left( {\sum\limits_{i = 1}^n {{x_i}{{\bf{v}}_i}} } \right)}^2} - \sum\limits_{i = 1}^n {{{\left( {{x_i}{{\bf{v}}_i}} \right)}^2}} } \right]

其中，代表element-wise product，因此的维度等于的维度。
2:Hidden Layers
$\begin{array}{l} {{\bf{z}}_1} = {\sigma_1}\left( {{{\bf{W}}_1}{{\mathop{\rm f}\nolimits}_{BI}}\left( {{{\bf{v}}_x}} \right) + {{\bf{b}}_1}} \right)\\ {{\bf{z}}_2} = {\sigma_2}\left( {{{\bf{W}}_2}{{\bf{z}}_1} + {{\bf{b}}_2}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;......\\ {{\bf{z}}_L} = {\sigma_L}\left( {{{\bf{W}}_L}{{\bf{z}}_2} + {{\bf{b}}_L}} \right) \end{array}$
3:Prediction Layer

$\begin{array}{l} {{\hat y}_{NFM}}\left( {\bf{x}} \right) = {w_0} + \sum\limits_{i = 1}^m {{x_i}{w_i} + {{\bf{h}}^{\rm{T}}}{\sigma_L}\left( {{{\bf{W}}_L}\left( {...{\sigma_1}\left( {{{\bf{W}}_1}{{\mathop{\rm f}\nolimits}_{BI}}\left( {{{\bf{v}}_x}} \right) + {{\bf{b}}_1}} \right)...} \right) + {{\bf{b}}_L}} \right)} \end{array}$

NFM算法可退化为FM算法，将向量置为全1的向量，即有：
$\begin{array}{l} {{\hat y}_{NFM - 0}}\left( {\bf{x}} \right) = {w_0} + \sum\limits_{i = 1}^m {{x_i}{w_i} + {{\bf{h}}^{\rm{T}}}\sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {{x_i}{{\bf{v}}_i} \odot {x_j}} } {{\bf{v}}_j}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = {w_0} + \sum\limits_{i = 1}^m {{x_i}{w_i} + \sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {\sum\limits_{f = 1}^k {{h_f}{v_{if}}{v_{jf}} \cdot {x_i}{x_j}} } } } \end{array}$

DCN

简介： 目前FM、FFM、DeepFM和PNN算法都只计算了2阶交叉，对于更高维度的交叉特征只能通过deep部分去学习。因此作者提出了Deep&cross network，可以任意组合特征，而且不增加网络参数。
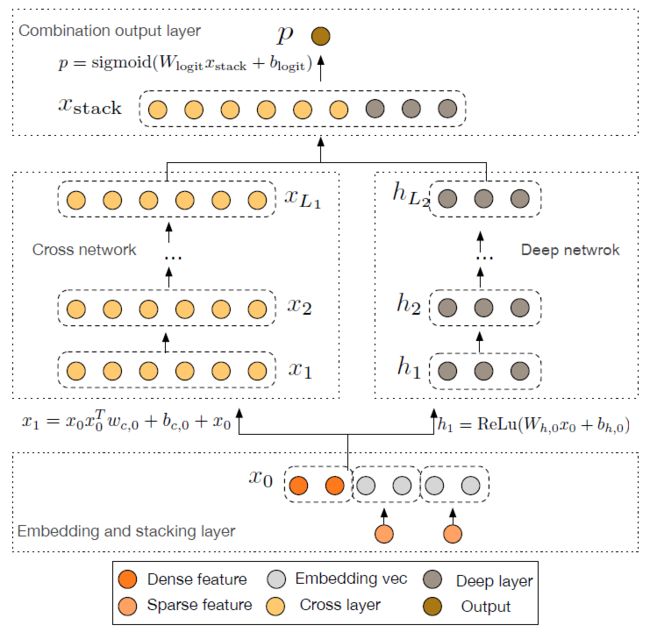
网络结构
1:embedding and stacking layer
将稀疏特征用embedding进行表示，比如：country=USA，以一个稠密向量表示USA这个特征，然后将所有的特征concatenate为一个向量用于表示输入。这里将dense特征和embedding特征一起concatenate，然后做为模型的输入。

2: cross layer
借鉴于residual network的思想，在每一层网络对特征进行交叉

{{\bf{x}}_{l + 1}} = {{\bf{x}}_0}{\bf{x}}_l^T{{\bf{w}}_l} + {{\bf{b}}_l} + {{\bf{x}}_l} = {\mathop{\rm f}\nolimits} \left( {{{\bf{x}}_l},{{\bf{w}}_l},{{\bf{b}}_l}} \right) + {{\bf{x}}_l}

3: deep layer

，其中为relu激活函数。
4:combination output layer
将经过cross layer的输出x和经过deep layer的输出h进行concat得到最终的特征向量。

xDeepFM

简介： DCN模型做特征交叉时采用的是特征内积，我们知道inner product得到的是一个标量。

去掉偏执项后有
$\begin{array}{l} {{\bf{x}}_{i + 1}} = {{\bf{x}}_0}{\bf{x}}_i^{\mathop{\rm T}\nolimits} {{\bf{w}}_{i + 1}} + {{\bf{x}}_i}\\ \;\;\;\;\; = {{\bf{x}}_0}\left( {{{\left( {{\alpha ^i}{{\bf{x}}_0}} \right)}^T}{{\bf{w}}_{i + 1}}} \right) + {\alpha ^i}{{\bf{x}}_0}\\ \;\;\;\;\; = {\alpha ^{i + 1}}{{\bf{x}}_0} \end{array}$

是一个标量，因此多层之后仍是与标量的乘积，并且特征交叉只是bit-wise级。
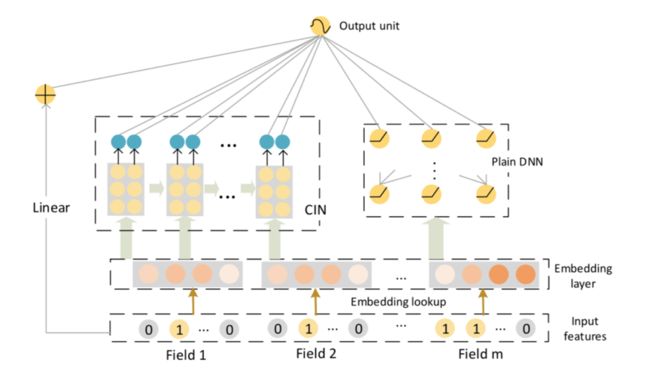
本文通过vector-wise级进行交叉计算，并且不会带来过高的计算复杂度。从图中可以看出，整个模型由三部分组成，分别是线性层、CIN(Compressed Interaction Network)和DNN，整体结构仍然属于wide&deep架构。
根据前一层隐层的状态和原特征矩阵，计算出一个中间结果，它是一个三维的张量。

其中，代表field个数，代表第层的特征向量个数，类似于CNN中的filter，而矩阵外积之后的矩阵就是需要卷积的image，就是一个feature map。

其中，。这样，我们就得到一个pooling vector：。hidden layers的所有polling vectors在连接到output units之前会被concatenated：，表示网络的深度。

总结: 从LR到xDeepFM算法，模型的优化主要在于从wide和deep两方面去获得更多更合理的交叉特征。wide部分的优化从ploy2、FM、FFM、AFM算法的二阶交叉到DCN、xDeepFM的高阶交叉；deep部分的优化从FNN对embedding进行concatenate，到PNN对embedding进行inner product、outer product，再到NFM对embeding进行bi_interaction。为了获得更好的效果，目前主流的深度学习算法大都采用wide&deep框架，同时结合wide部分和deep部分的优点。
模型复杂度

model	Number of Parameters
LR	m
Poly2	m + H
FMs	m + m * K
FFMs	m + m * (n-1) * K
FwFMs	m + m * K + n * (n-1)/2
AFM	m + m * K + K * H1 + H1 * 2 + K
FNN	1 + n + n * k + (1 + f + f * k) * H1 + H1 * H2 + H2 * 1
IPNN	1 + n + n * k + (1 + f + f * k) * H1 + H1 * H2 + H2 * 1
OPNN	1 + n + n * k + (1 + f + f * k) * H1 + H1 * H2 + H2 * 1
Wide&deep	1 + n + n * k + f * k * H1 + H1 * H2 + H2
deepFM	1 + n + n * k + f * k * H1 + H1 * H2 + H2 * 1
NFM	1 + n + n * k + k * H1 + H1 * H2 + H2 * 1
DCN	1 + n + 2 * d * Lc + d * (m + 1) + m * (m + 1) * (Ld - 1) + 1 + d + m
xDeepFM	1 + n + k * H1 * f + H1 * H2 + H2 * 1 + H2 * (1 + H1 * f)

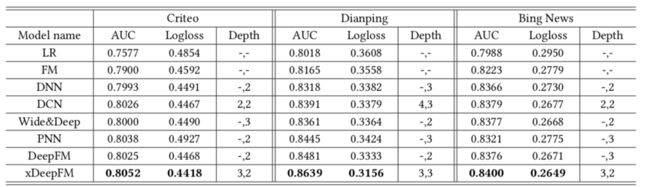
模型效果

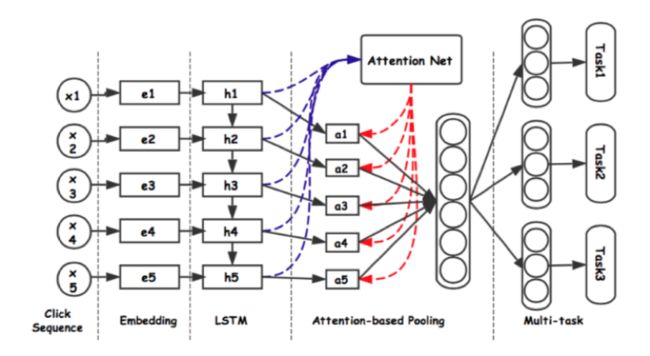
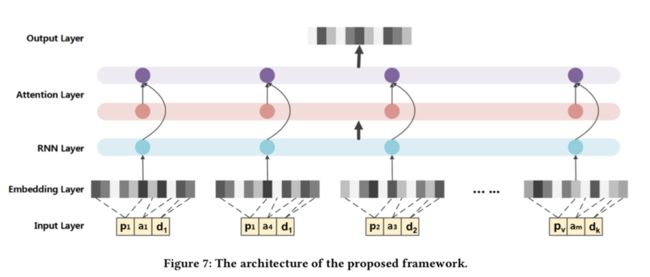
DUPN

简介： 前面列举的算法都是针对单点数据，而用户的行为序列一定程度上代表了用户当前的兴趣，但是行为序列中不是每一次行为都是同等重要的。每一次行为对每一个用户的重要程度都是不同的，因此本文通过user对行为序列做attention计算得到一个user embedding，为了获得更加通用的user embedding，作者将该user embedding应用到多个任务做multi-task建模。
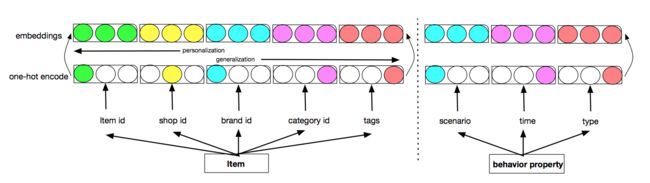
输入item节点特征包含：

{a_t} = \frac{{\exp \left( {{\mathop{\rm attention}\nolimits} \left( {{{\bf{h}}_t},q,u,\omega } \right)} \right)}}{{\sum\nolimits_{t = 1}^T {\exp \left( {{\mathop{\rm attention}\nolimits} \left( {{{\bf{h}}_t},q,u,\omega } \right)} \right)} }}

是一个两层的全连接层。

RIB

简介： RIB模型和DUPN网络结构类似于，不同之处在于attention计算。另外本文输入特征中加入商品页停留时间特征、用户行为（点击、浏览、购买、加入购物车）和哪个模块进入商品页，具体特征如下：

Var	Attribute	Description
	Product ID	SKU(Stock Keeping Unit)
	Category ID	Product category
	Home2Product	Enter from homepage
	ShopList2Product	Enter from category page
	Sale2Product	Enter from sale page
	Cart2Product	Enter from carted page
	SearchList2Product	Enter from searched results
	Detail_comments	In comment module
	Detail_specification	In specification module
	Detail_bottom	At the bottom
	Cart	Add to cart
	Order	Order
	Dwell time	0 9 seconds
	Dwell time	1024 seconds
	Dwell time	2560 seconds
	Dwell time	61120 seconds
	Dwell time	120 seconds

其中attention计算为：

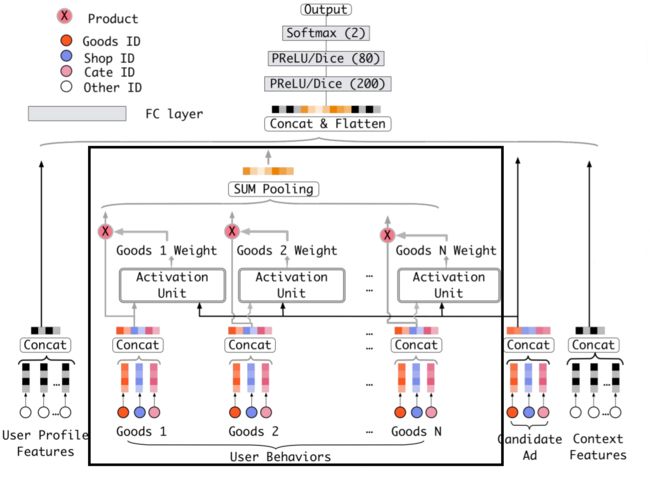
DIN

简介： 与DUPN、RIB算法不同，本文并未采用GRU网络对用户历史行为序列进行建模，而是直接通过attention对行为序列进行加权。DIN模型通过当前item对用户历史行为数据进行加权求和计算用户表征向量，这里通过dice激活函数计算历史行为的权重。与候选广告商品相关的行为赋予更高的权重，对用户兴趣的表示起主要作用。
1:用户历史行为向量

{{\bf{v}}_{\rm{U}}}\left( {\bf{A}} \right) = {\mathop{\rm f}\nolimits} \left( {{{\bf{v}}_A},{{\bf{e}}_1},{{\bf{e}}_2},...,{{\bf{e}}_H}} \right) = \sum\limits_{j - 1}^H {{\mathop{\rm a}\nolimits} \left( {{{\bf{e}}_j},{{\bf{v}}_A}} \right)} {{\bf{e}}_j} = \sum\limits_{j = 1}^{\rm{H}} {{{\bf{w}}_j}{{\bf{e}}_j}}

其中，代表用户行为向量，代表广告embedding向量。
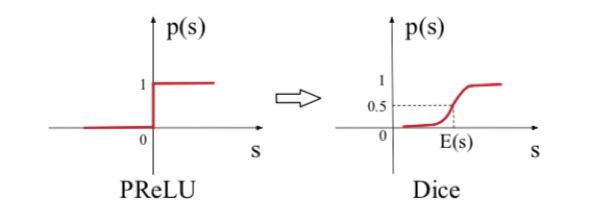
2:activation function
RELU激活函数从0点进行分割，大于0原样输出，小于0输出为0，这样将会导致模型更新缓慢，因此它的改进版PRELU，又叫LeakyRELU的出现，它修正了小于0输出为0的问题，即使小于0也能更新网络参数，加快模型收敛。但是它仍然是在0点进行分割，数据分割应该是随着数据而自适应的变化，因此作者提出了PRELU的改进版Dice。

3:自适应归一化
不归一化时，SGD只需要更新mini-batch中非零稀疏特征。但是加入l2归一化之后，每个mini-batch需要计算所有参数，这将会导致计算负担加重。在CTR任务中，特征较为稀疏并且维度较高，大部分特征只出现几次，而小部分特征出现很多次，即长尾分布，这将会导致模型过拟合。一个较为直接的方式，对出现次数较少的特征进行截断，但是这样将会导致信息的丢失，因此作者提出了一种根据特征频次自适应的更新方式。
1:出现频次较高的特征给予较小的正则化强度
2:出现频次较高的特征给予较高的正则化强度

{{\bf{w}}_j} \leftarrow {{\bf{w}}_j} - \eta \left[ {\frac{1}{{\left| {{{\rm B}_m}} \right|}}\sum\limits_{\left( {x,y} \right) \in {{\rm B}_m}} {\frac{{\partial L\left( {p\left( x \right),y} \right)}}{{\partial {{\bf{w}}_j}}} + \lambda \frac{{{\alpha _{mj}}}}{{{n_j}}}{{\bf{w}}_j}} } \right]

DIEN

简介： din算法对用户历史行为通过当前item计算attention，获得最终的user embedding，整个算法计算简单，易于理解。但是模型忽略了用户行为之间的关联关系，因此本文用一个GRU网络(兴趣提取模块)来计算用户兴趣的关联关系。DUPN算法也是通过一个GRU网络计算用户历史行为，然后通过一个additional attention进行加权求和获得最终的user embedding，本文思路与DUPN类似，整体结构仍然是通过GRU计算用户历史行为，然后通过一个attention对不同行为item进行加权求和，得到最终的user embedding，不同之处在于本文通过另一个GRU对时序数据更新进行控制。
Auxiliary loss

{L_{aux}} = - \frac{1}{N}\left( {\sum\limits_{i = 1}^N {\sum\limits_t {\log \sigma \left( {{{\bf{h}}_t},{\bf{e}}_b^i\left[ {t + 1} \right]} \right)} } } \right) + \log \left( {1 - \sigma \left( {{{\bf{h}}_t},{\bf{\hat e}}_b^i\left[ {t + 1} \right]} \right)} \right)

为了充分利用用户历史不同的时刻行为，作者在每个时刻加入auxiliary loss用于表征用户的兴趣(用户点击item为正、随机采样候选集为负)。
Attention

，其中通过候选item和gru输出计算attention权重。
Interest Evolving Layer
GRU with attentional input (AIGRU)

Attention based GRU(AGRU)

GRU with attentional update gate (AUGRU)

我们常用attention与GRU输出进行加权求和得到最终的特征表示，但是本文通过另一个GRU网络对第一个GRU网络的输出进行建模，通过attention计算得到当前item与历史行为item的相关度，然后通过该相关度得分做节点更新约束，如果与当前相关性较弱，则趋近于零，状态不更新，最后取最终的状态输出作为最终的特征输出(作者尝试了3种不同类型的Interest Evolving Layer )。

参考文献

[1]Factorization Machines
[2]Field-aware Factorization Machines for CTR Prediction
[3]Wide & Deep Learning for Recommender Systems
[4]Deep Learning over Multi-Field Categorical Data: A Case Study on User Response Prediction
[5]Product-based Neural Networks for User Response Prediction
[6]DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
[7]Neural Factorization Machines for Sparse Predictive Analytics
[8] Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks
[9]Deep & Cross Network for Ad Click Predictions
[10]Deep Interest Network for Click-Through Rate Prediction
[11]Field-aware Factorization Machines for CTR Prediction
[12]Field-weighted Factorization Machines for Click-Through Rate Prediction in Display Advertising
[13] Micro Behaviors: A New Perspective in E-commerce Recommender Systems
[14] xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems