我们开始介绍“二叉树和递归”。递归,是使用计算机解决问题的一种重要的思考方式。而二叉树由于其天然的递归结构,使得基于二叉树的算法,均拥有着递归性质。使用二叉树,是研究学习递归算法的最佳入门方式。在这一章里,我们就来看一看二叉树中的递归算法。
在前面知识的学习中,我们看到了在基础算法以及系统设计中都用到了递归。深度优先遍历中也用到了递归。从这一部分开始,我们从另一个视角看递归。
从二叉树的角度看递归
二叉树天然具有递归的性质。二叉树的定义就是用二叉树定义二叉树。对于二叉树的定义来说,应该补充一点:空是一棵二叉树。
下面,我们来观察一个二叉树的前序遍历的递归方法。
Java 代码:
public void preorder(TreeNode node){
if(node != null){
System.out.print(node.val);
preorder(node.left);
preorder(node.right);
}
}
注意:这里 System.out.print(node.val); 这一行代码表示“处理这个结点的逻辑”。
在这里,我们先强调编写递归函数的第 1 个注意事项:首先明确这个函数要表达的任务(逻辑),明确参数的定义和返回值的意义。
接下来,我们将上面的代码改造一下。
Java 代码:
public void preorder(TreeNode node){
// 先写递归终止条件
if(node == null){
return;
}
// 再写递归过程
System.out.print(node.val);
preorder(node.left);
preorder(node.right);
}
其实这样的写法更像递归结构,因为对于我们定义的每一个递归函数来说,应该包含下面两个部分:1、递归终止条件;2、设立递归过程,定义清楚函数的语义。
这就是我们编写一个递归函数应该注意的第 2 件事情。
接下来,我们再看一个方法:在一个二叉树中查看是否存在一个键值。写这个递归方法的步骤:想想(1)递归终止条件是什么?(2)递归过程是什么?参数 Node node 是什么意思?我们这里定义的参数 Node 对象,是在以 node 为根结点的二叉树中寻找指定的 key。于是,我们的逻辑是:如果 node 本身不是我们要找的结点的话,我们继续在 node 的左孩子和右孩子中继续查找。
Java 代码:
public boolean contain(Node node, int key) {
// 首先我们要处理递归到底的情况
if (node == null) {
return false;
}
if (key == node.key) {
return true;
}
if (contain(node.left, key) || contain(node.right, key) {
return true;
}
return false;
}
那么,我们可以再想想如何释放以 Node 为根结点的二叉树?
例题
例1:LeetCode 第 104 题:求一棵二叉树的最大深度。
传送门:英文网址:104. Maximum Depth of Binary Tree ,中文网址:104. 二叉树的最大深度 。
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 7返回它的最大深度 3 。
关键:要能看出这道题本质上是二叉树的后序遍历。
Python 代码:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
# 先计算左右子树,然后再计算自己,这是后序遍历
l_sub_tree_depth = self.maxDepth(root.left)
r_sub_tree_depth = self.maxDepth(root.right)
return max(l_sub_tree_depth, r_sub_tree_depth) + 1
Python 代码:把上面的递归改成循环
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
depth = 0
stack = [(1, root)]
while stack:
cur_depth, node = stack.pop()
depth = max(depth, cur_depth)
if node.left:
stack.append((cur_depth + 1, node.left))
if node.right:
stack.append((cur_depth + 1, node.right))
return depth
说明:这个写法看一看就好,感觉没啥意思。
感觉递归调用就像什么都没有做一样。通过这个例子,我们来理解一下(1)(2)这两个步骤的具体应用。这让我想起了八皇后问题。
还可以使用 DFS 和 BFS 完成这个问题。首先 BFS 我觉得思路更直接一些,代码也是有套路的。
Python 代码:
class Solution(object):
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
depth = 0
queue = [root]
while queue:
size = len(queue)
depth += 1
for _ in range(size):
first = queue.pop(0)
if first.left:
queue.append(first.left)
if first.right:
queue.append(first.right)
return depth
Python 代码:使用 DFS
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# 求一棵二叉树的最大深度。
# 要能看出这道题本质上是二叉树的后序遍历。
class Solution(object):
def __init__(self):
self.max_depth = 0
def maxDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
self.__dfs(root, 0)
return self.max_depth
def __dfs(self, node, depth):
if node is None:
return
depth += 1
if node.left is None and node.right is None:
# 到叶子结点了,可以结算了
self.max_depth = max(self.max_depth, depth)
return
if node.left:
self.__dfs(node.left, depth)
if node.right:
self.__dfs(node.right, depth)
- 复习和二叉树相关的所有操作。
练习
练习1:LeetCode 第 111 题:求一棵二叉树的最小深度。
传送门:英文网址:111. Minimum Depth of Binary Tree ,中文网址:111. 二叉树的最小深度 。
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树
[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 7返回它的最小深度 2.
分析:即求一棵二叉树从根结点到叶子结点的最短路径的长度。
这个问题里面有小的陷阱。
我们在思考递归终止条件的时候,有的时候可能会存在陷阱。
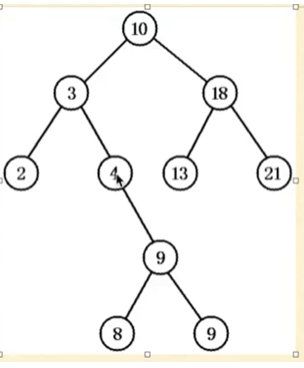
这道题,我第一次做是想当然,顺着第 104 题把最大改成最小,但是要注意到上图 4 那个结点,4 的左孩子为空,返回 0 ,右孩子为 9,返回2,按照我们的逻辑就返回 0 ,显然是错误的,所以要针对左右孩子有一个为空的时候,做出分类判断。
Python 代码:
# Definition for a binary tree node.
# 111. 二叉树的最小深度
# 给定一个二叉树,找出其最小深度。
#
# 最小深度是从根结点到最近叶子结点的最短路径上的结点数量。
#
# 说明: 叶子结点是指没有子结点的结点。
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
if root.left is None:
return 1 + self.minDepth(root.right)
if root.right is None:
return 1 + self.minDepth(root.left)
return 1 + min(self.minDepth(root.left), self.minDepth(root.right))
Python 代码:使用 BFS:==使用层序遍历,我感觉更直接一些,因为只要扫到叶子结点,就可以返回了==
class Solution(object):
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
depth = 0
queue = [root]
while queue:
depth += 1
size = len(queue)
for _ in range(size):
first = queue.pop(0)
if first.left is None and first.right is None:
return depth
if first.left:
queue.append(first.left)
if first.right:
queue.append(first.right)
Python 代码:使用 DFS
# Definition for a binary tree node.
# 111. 二叉树的最小深度
# 给定一个二叉树,找出其最小深度。
#
# 最小深度是从根结点到最近叶子结点的最短路径上的结点数量。
#
# 说明: 叶子结点是指没有子结点的结点。
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def __init__(self):
self.min_depth = float("inf")
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if root is None:
return 0
self.__dfs(root, 0)
return self.min_depth
def __dfs(self, node, depth):
if node is None:
return
depth += 1
if node.left is None and node.right is None:
self.min_depth = min(self.min_depth, depth)
return
if node.left:
self.__dfs(node.left, depth)
if node.right:
self.__dfs(node.right, depth)
(本节完)