【详解+推导！！】DQN

DQN，Deep Q-Network 是Q-Learning和深度网络结合的一种算法，在很多强化学习问题中表现优异。在看DQN之前建议先了解一下Q-Learning的基本原理：https://blog.csdn.net/qq_33302004/article/details/114871232
也可以看一下value-based 和 policy-based 方法的基本介绍:https://blog.csdn.net/qq_33302004/article/details/115189857

1. 简单介绍

DQN 是一种 value-based 方法，与 policy Gradient 不同，网络学习的不是策略，而是要学习成为一个Critic，其策略就是选择当前状态$s$下，评分最高的$a$。

这里面有两个关键的符号表示：

• $V^{\pi }(s)$ 和 $Q^{\pi }(s,a)$；
• 其中$\pi$是指某一种策略，我们的Critic是针对特定的策略而言的，同样的$s$，$a$，如果是不同的$\pi$，Critic也会给出不同的值。例如棋魂中：
  $$\begin{array}{rl}& V^{以前的阿光}(大马步飞)=bad\\ & V^{现在的阿光}(大马步飞)=good\end{array}$$
• 其中$V^{\pi }(s)$ 表示的是actor在状态$s$下的累计回报期望（cumulated reward expects ）；
• $Q^{\pi }(s,a)$表示的是actor在状态$s$下选择状态$a$的累计回报期望。

传统Q-Learning中会建立一个表格，存储下所有$Q^{\pi }(s,a)$的值，在决策的时候通过查表的方式决定选择那种action，但是在实际中，$s$和$a$的取值空间可能很大，无法将所有state都打成表格，所以就有了结合深度网络的方法，也就是我们本文所讲的DQN。其$Q^{\pi }(s,a)$不使用表格存储，而是训练一个神经网络，输入$s$和$a$，输出$Q^{\pi }(s,a)$的值。

2. MC 和 TD 方法

那么如何计算$V^{\pi }(s)$ 的值呢？

通常有两种方法：MC-based方法（蒙特卡罗）和TD-based方法（时间差分）。

Monte-Carlo(MC)-based的方法，就是让actor与环境一直互动，我们就可以统计出接下来的累计回报会有多大，通过多个episode的采样，就可以计算出累计回报期望$G$。

所以如果想要使用神经网络+MC方法实现的话会很直观，这就是一个回归问题（regression），只要有监督学习就可以啦。

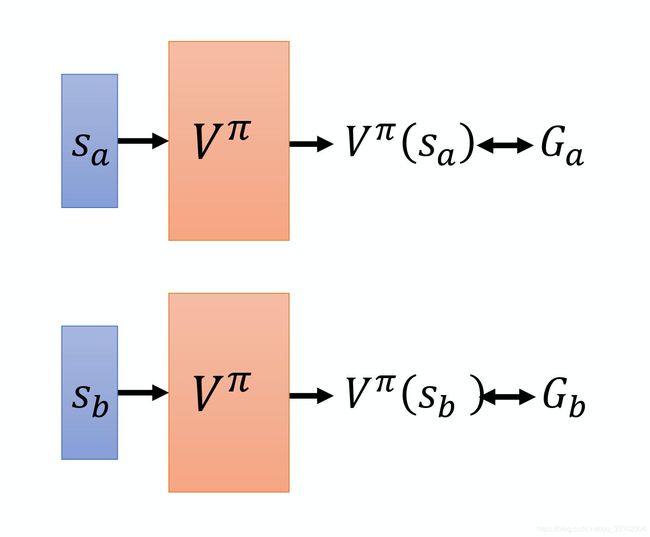
网络的输出就是一个值，你希望在输入$s_a$的时候，输出的值跟$G_a$越近越好，输入 $s_b$ 的时候，输出的值跟$G_b$越近越好。接下来把网络训练下去，就结束了。这是 MC-based 的方法。

Temporal-difference(TD)-based 的方法

MC方法存在一个问题，就是每次我们在计算累计回报的时候，都需要从某个状态$s_a$一直玩到游戏结束，这样才能得到所有奖励的总和。但是有些游戏玩完一把的时间很长，如果要玩到游戏结束才更新网络的话花费的时间太长了，而TD-based方法可以解决这个问题。

TD-based 的思想是基于下面的式子而来的：
$$V^{\pi }(s_t)=V^{\pi }(s_{t+1})+r_t$$

假设我们有某个策$\pi$，它在状态$s_t$会选择动作$a_t$进入状态$s_{t+1}$（这是一种确定的policy，$s_t$的下一个状态一定是$s_{t+1}$，而不是其他状态）。所以这两个状态的值函数的关系就是$V^{\pi }(s_t)=V^{\pi }(s_{t+1})+r_t$，那我们只需要训练一个可以计算$V^{\pi }$的网路，通过网络求得$V^{\pi }(s_t)$和$V^{\pi }(s_{t+1})$的值，让二者的差值接近$r_t$即可。

如今在使用中TD方法用得比较多。

3. Q-Function

上面是用网络训练出一个$V^{\pi }$，还有一种思路就是利用网络训练处$Q^{\pi }$，$Q^{\pi }$的训练有两种方法：

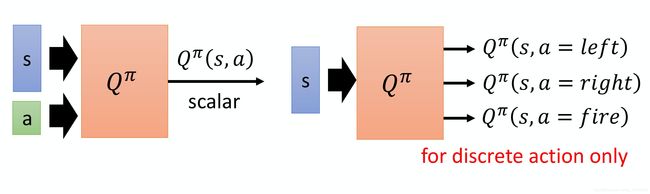
• 一种是输入$s$和$a$，输出一个标量（scalar），也就是$Q^{\pi }(s,a)$的值；
• 另一种是输入$s$，输出是一个向量（vector），是每一个action的$Q^{\pi }(s,a)$的值，但是这个方法只适用于动作是离散的，如果动作是连续的则无法表示。

4. DQN的大致过程

• 首先我们可以初始化一个$Q^{\pi }$网络，我们的actor其实就是$\pi (s)=\underset{a}{\mathrm{argmax}}Q(a,s)$；
• 利用这个actor去与环境做互动，产生data；
• 接下来利用收集到的data去更新$Q^{\pi }$网络，这里面可以使用TD或者MC的方法估计累计回报期望；
• 因为acotr是$\pi (s)=\underset{a}{\mathrm{argmax}}Q(a,s)$，所以$Q^{\pi }$更新了，actor也就随之更新了；
• 接下来再用新的actor去与环境做互动，产生数据、更新$Q^{\pi }$，互动、产生数据、更新，一直循环下去就会越来越好。

5. 常用Tips

（1）Target Network

在DQN中计算Q-function一般采用TD的方式， 其过程是这样的：

• 首先，我们收集到一个data：当前状态$s_t$，采取的动作$a_t$，得到的回报$r_t$，跳到的下一个状态为$s_{t+1}$；
• 我们要训练的网络可以理解为一个函数，就是$Q^{\pi }(s,a)$，输入s和a，输出value值；
• 所以我们可以先给网络喂入$s_t$和$a_t$计算得到$Q^{\pi }(s_t,a_t)$，再喂入$s_{t+1}$和$\pi (s_{t+1})$计算得到$Q^{\pi }(s_{t+1},\pi (s_{t+1}))$，那么二者的关系如下：
  $$Q^{\pi }(s_t,a_t)=r_t+Q^{\pi }(s_{t+1},\pi (s_{t+1}))$$
• 我们在训练网络的时候，把等号右边的值作为label，这样就变成了一个回归问题，进行有监督训练即可。

但是我们可以观察到，随着网络的更新，等号右边的值$r_t+Q^{\pi }(s_{t+1},\pi (s_{t+1}))$是会改变的，让网络去拟合一个一直在变的目标，会导致训练不太稳定，获得的结果也不好。

所以这个Tips的思路就是，将等式右边的$Q^{\pi }$固定住，在训练的时候，只更新左侧$Q^{\pi }$的参数，而不更新右侧$Q^{\pi }$的参数，这样就可以保证网络的拟合目标稳定。因为右侧的$Q^{\pi }$负责产生目标，所以就叫做目标网络。

在实现过程中，会固定右侧的网络，去多次更新左侧的网络，更新一定次数后，再用左侧网络替换右侧网络。

（2）Exploration

探索（exploration）是强化学习中要重点考虑的一个事情，因为强化学习的主要思路就是通过不断试错而获得好的结果，如果我们的探索策略会导致某些情况不可达，这回导致我们的网络无法学习那些情况的知识。

而从我们前文中的讲述可以看出，我们的actor：$\pi (s)=\underset{a}{\mathrm{argmax}}Q(a,s)$是一种固定的策略，这会导致我们与环境互动的时候很局限。这里有两种方法为探索增加随机性：

1. Epsilon Greedy，我们设一个$ϵ$值，比如0.1，表示在每次决策的时候在[0,1]区间内uniform一个随机数，如果小于0.1，就是random一个action，其余的情况就采用$\pi (s)=\underset{a}{\mathrm{argmax}}Q(a,s)$。
2. Boltzmann Exploration，这个方法的思路就是输出一个动作空间上的概率分布，再根据概率分布去做采样，采样的概率如下：
   $$p(a|s)=\frac{\exp (Q(s,a))}{{\sum }_a\exp (Q(s,a))}$$

（3）Experience Replay

**Experience Replay(经验回放)**会构建一个 Replay Buffer，Replay Buffer 又被称为 Replay Memory。Replay Buffer 里面会存放很多数据，每一个数据由$(s_t,a_t,r_t,s_{t+1})$组成。这个Repaly Buffer里面的experience可能来自不同的策略采样结果，比如Repaly Buffer可以存5万组数据，而我们每次与环境互动会产生1万组数据，只有当Buffer满了的时候才会丢掉旧的experience。

在使用过程中，会用当前的策略$\pi$与环境互动，把产生的经验压入buffer，然后再采样若干个batch去训练$Q^{\pi }$网络。然后再用新的策略互动、采样、训练，如此循环。

这里我们会有一个疑问，我们要训练的网路是$Q^{\pi }$，而观测值的采样不来自于$\pi$，这样会不会有问题？
目前给出的回答是没关系的，因为我们并不是去采样一个 trajectory，我们只采样了一次的经验$(s_t,a_t,r_t,s_{t+1})$，这跟是不是 off-policy 这件事是没有关系的，就算是off-policy，这些经验不来自于$\pi$我们也可以直接用来训练$Q^{\pi }$。具体解释我也不是很清楚，理论上应该是可以解释通的，大家如果知道具体解释欢迎留言。

Experience Replay 的好处有两个：

1. 这样做可以更加充分的利用采样数据。在强化学习中花时间最多的步骤往往是和环境互动，而传统的方法中采样到的数据被使用了一次就丢掉了，通过replay buffer我们可以减少和环境的互动次数的同时，仍然保留充足训练数据，这样可以让经验的利用更加高效。
2. 第二个好处，在训练网络的时候，其实我们希望一个 batch 里面的数据越多样(diverse)越好。如果你的 batch 里面的数据都是同样性质的，你训练下去是容易坏掉的。如果 batch 里面都是一样的数据，你训练的时候，performance 会比较差。我们希望 batch 的数据越多样越好。那如果 buffer 里面的那些经验通通来自于不同的策略，那你采样到的一个 batch 里面的数据会是比较多样的。

6.DQN算法流程