第七届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第七届蓝桥杯大赛个人赛决赛（C/C++大学B组）

第一题 一步之遥（15分）

从昏迷中醒来，小明发现自己被关在X星球的废矿车里。

矿车停在平直的废弃的轨道上。

他的面前是两个按钮，分别写着“F”和“B”。

小明突然记起来，这两个按钮可以控制矿车在轨道上前进和后退。

按F，会前进97米。按B会后退127米。

透过昏暗的灯光，小明看到自己前方1米远正好有个监控探头。

他必须设法使得矿车正好停在摄像头的下方，才有机会争取同伴的援助。

或许，通过多次操作F和B可以办到。

矿车上的动力已经不太足，黄色的警示灯在默默闪烁…

每次进行 F 或 B 操作都会消耗一定的能量。

小明飞快地计算，至少要多少次操作，才能把矿车准确地停在前方1米远的地方。

请填写为了达成目标，最少需要操作的次数。

注意，需要提交的是一个整数，不要填写任何无关内容（比如：解释说明等）

• 答案：97

思路：暴力枚举

1. 即求min(F+B|97F-127B==1)，在0~100内暴力枚举F，B，如有答案就是最小的了，如果没有则将范围放大
2. 这里为答案是97，为了保险起见将范围扩到到0~1000确保安全

代码实现

#include
#include
#define N 1000
using namespace std;

int main(){
     
	int min=2*N+1;
	for(int B=0;B<=N;B++){
     
		for(int F=0;F<=N;F++){
     
			if(97*F-127*B==1){
     
				if(F+B<min){
     
					min=F+B; 
					cout<<"F:"<<F<<" B:"<<B<<endl;
				} 
			}
		}
	}
	cout<<min;
	return 0;
}

第二题 凑平方数（35分）

把0~9这10个数字，分成多个组，每个组恰好是一个平方数，这是能够办到的。
比如：0, 36, 5948721

再比如：
1098524736
1, 25, 6390784
0, 4, 289, 15376
等等…

注意，0可以作为独立的数字，但不能作为多位数字的开始。
分组时，必须用完所有的数字，不能重复，不能遗漏。

如果不计较小组内数据的先后顺序，请问有多少种不同的分组方案？

注意：需要提交的是一个整数，不要填写多余内容。

• 答案：223

思路：枚举

1. 枚举0~100000的平方
2. 每枚举出一个平方数将它筛选：每一位的数字都不同的留下来
3. 将通过筛选的所有平方数放入数组num里面（此时必是升序的）
4. 尝试num的所有组合，筛选出所有位不同，刚好10个数字都用上的进行计数。

代码实现

#include
#include
using namespace std;

int sign[10];
long long t[10];
long long num[100000];
int n=1;

//筛选器 
bool filter(int n){
     
	int location[10];
	for(int i=0;i<10;i++) location[i]=0;
	int weight=10,temp,a;
	for(int i=1;true;i*=weight){
     
		temp=n/i;
		if(temp==0) break;
		a=temp%10;
		if(location[a]==1) return false;
		location[a]=1;
	}
	return true;
}

//放置数字 
bool put_num(int n,int place){
     
	int weight=10,temp,a;
	if(n==0){
     
		sign[0]=1;
		t[0]=0;
		return true;
	}
	for(int i=1;true;i*=weight){
     
		temp=n/i;
		if(temp==0) break;
		a=temp%10;
		if(sign[a]==1)
			return false;
	}
	for(int i=1;true;i*=weight){
     
		temp=n/i;
		if(temp==0) break;
		a=temp%10;
		sign[a]=1;
	}
	t[place]=n;
	return true;
}

//取消放置数字 
void cancel(int n,int place){
     
	int weight=10,temp,a;
	if(n==0){
     
		sign[0]=0;
		t[0]=-1;
		return;
	}
	for(int i=1;true;i*=weight){
     
		temp=n/i;
		if(temp==0) break;
		a=temp%10;
		sign[a]=0;
	}
	t[place]=-1;
}

//深度优先遍历 
int dfs(int index,int place){
     
	int len = 0; 
	int count = 0;
	int max=10; 
	for(int i=0;i<10;i++) len+=sign[i];
	//cout<<"放置了"<
	if(len==10) {
     
		//cout<<"找到一个组合"<
		for(int i=0;t[i]!=-1;i++) cout<<t[i]<<" ";
		cout<<endl;
		return 1;
	}
	if(index>=n) return 0;
	for(int i=0;i<10-len;i++)					//剪枝 
		max *= 10;
	for(int i=index;i<n;i++){
     
		if(num[i]>max) break;
		if(!put_num(num[i],place)) continue;	//放不下了直接继续下一情况 
		count += dfs(i+1,place+1);				//放下了继续放统计结果 
		cancel(num[i],place);					//回溯 
	}
	return count; 
}

int main(){
     
	long long temp;
	int count=0;
	//1.枚举0~99999的平方 
	num[0]=0;
	for(long long i=1;i<100000;i++){
     
		temp=i*i;
	//2.通过筛选的放入数组num中 
		if(filter(temp)) num[n++]=temp; 
	}
	cout<<"共有"<<n<<"个各位不同的平方数"<<endl; 
	//for(int i=0;i
	//cout<
	//3.尝试所有组合并计算可能的组合数
	for(int i=0;i<n;i++){
     
		for(int j=0;j<10;j++){
     		//清空标记
			sign[j]=0;	
			t[j]=-1; 
		} 
		put_num(num[i],0);
		count+=dfs(i+1,1);
	} 
	cout<<count;
	return 0;
} 

• 运行结果截图

第三题 棋子换位（25分）

有n个棋子A，n个棋子B，在棋盘上排成一行。
它们中间隔着一个空位，用“.”表示，比如：

AAA.BBB

现在需要所有的A棋子和B棋子交换位置。
移动棋子的规则是：

1. A棋子只能往右边移动，B棋子只能往左边移动。
2. 每个棋子可以移动到相邻的空位。
3. 每个棋子可以跳过相异的一个棋子落入空位（A跳过B或者B跳过A）。

AAA.BBB 可以走法：

移动A ==> AA.ABBB
移动B ==> AAAB.BB

跳走的例子：

AA.ABBB ==> AABA.BB

以下的程序完成了AB换位的功能，请仔细阅读分析源码，填写划线部分缺失的内容。

#include 
#include 

void move(char* data, int from, int to)
{
     
	data[to] = data[from];
	data[from] = '.';
}

int valid(char* data, int k)
{
     
	if(k<0 || k>=strlen(data)) return 0;
	return 1;
}
	
void f(char* data)
{
     
	int i;
	int tag;
	int dd = 0; // 移动方向
	
	while(1){
     
		tag = 0;
		for(i=0; i<strlen(data); i++){
     
			if(data[i]=='.') continue;
			if(data[i]=='A') dd = 1;
			if(data[i]=='B') dd = -1;
			
			if(valid(data, i+dd) && valid(data,i+dd+dd) 
			&& data[i+dd]!=data[i] && data[i+dd+dd]=='.'){
      
			//如果能跳... 
				move(data, i, i+dd+dd);
				printf("%s\n", data);
				tag = 1;
				break;
			}
		}
		
		if(tag) continue;
		
		for(i=0; i<strlen(data); i++){
     
			if(data[i]=='.') continue;
			if(data[i]=='A') dd = 1;
			if(data[i]=='B') dd = -1;			
				 
			if(valid(data, i+dd) && data[i+dd]=='.'){
      
			// 如果能移动...
				if( ______________________ ) continue;  //填空位置 
				move(data, i, i+dd);
				printf("%s\n", data);
				tag = 1;
				break;
			}
		}
		
		if(tag==0) break;					
	}
}
	
int main()
{
     
	char data[] = "AAA.BBB";	
	f(data);
	return 0;
}

注意：只提交划线部分缺少的代码，不要复制已有代码或填写任何多余内容。

- 答案：dd==1 && valid(data, i+dd+dd+dd) && data[i+dd+dd]==data[i+dd+dd+dd]
  				&& data[i]!=data[i+dd+dd] && data[strlen(data)/2]!='.'
  				|| strlen(data)/2%2==0 && i==strlen(data)-3 && data[strlen(data)-2]=='.' &&
  				data[strlen(data)-3] != data[strlen(data)-1]

  答案填data[4]=='.'&&i==3 && data[6]=='B'也可以，但是由于题目有如下说明，固上述答案是最稳妥的，无论AB有多少个，只要是数量上相等都能成功换位。

思路：逆向推导

1. 注释掉if条件直接运行会发现'.'卡在'AAA'的左边了，明显当'.'在连续2个A的左边而AA的右边还有B的时候是不可能成功交换的。
2. 猜想'BBB.AAA'是由'.ABABAB'得到的，由于固定代码部分有“能跳则跳”的规律，可轻松由'.ABABAB'得到'BBB.AAA'
3. 由'.ABABAB'逆推回'AAA.BBB'可以猜想'AAA.BBB'==>'.ABABAB'过程如下
   'AAA.BBB'==>'AA.ABBB'==>'AABA.BB'==>'AABAB.B'==>'A.BABAB'==>'.ABABAB'
   ​			       ①			②			③			④			 ⑤
   由'.ABABAB'==>'BBB.AAA'过程如下
   '.ABABAB'==>'BABABA.'==>'BABAB.A'==>'B.BABAA'==>'BB.ABAA'==>'BBBA.AA'==>'BBB.AAA'
   ​				 ⑥			  ⑦				⑧			⑨			⑩		    ▲
   观察上述过程，只有①、③、⑤、⑦、⑨以及▲是移动的，其余都是跳跃的，可以发现如果注释掉if那么除了③其他的移动都是遵循上述过程进行的，所以重点观察③
4. 如果注释掉if，③应该是'AABA.BB'==>'AAB.ABB'，就是说如果在条件中加一限制让原本应该让A移动的变成让B移动整个过程就会按上述过程进行了。
5. 最简单的方法就是把A移动的时候跳过，接下来i指向‘.’后边的B的时候B就移动了，故填data[4]=='.'&&i==3 && data[6]=='B'正好可以在③的初始情况的时候跳过A的移动
6. 由于题目要求通用性，继续对第3点的过程进行观察，发现③的情况具有如下特征
   - dd==1（当前i指向的是A）
   - '.'后两个字符的相同的
   - '.'前后的字符不同
7. 有了以上三个特征可以尝试用这三个条件作为continue的跳过条件，但是发现初始情况也会被跳过，故还需要加上不是初始情况的条件，即‘.’不在中间
8. 用以上4个条件已经可以完成AB的换位了，但是由于想要更好的通用性，增加1个A和1个B尝试，发现最后一个B没有交换成功，尝试加2个A和2个B，交换成功！猜想偶数个A和偶数B一定剩下1个B交换失败，奇数个则可以成功交换，经测试的确如此。
9. 观察偶数个的情况，有一步'...BA.B'==>'...B.AB',如果能变成==>'...BAB.'那么就可以将最后一个B交换了，即跳过移动A转而移动B，即可达到要求
10. 根据上述分析得到答案dd= =1 && valid(data, i+dd+dd+dd) && data[i+dd+dd]= =data[i+dd+dd+dd]
    				&& data[i]!=data[i+dd+dd] && data[strlen(data)/2]!='.'
    				|| strlen(data)/2%2==0 && i==strlen(data)-3 && data[strlen(data)-2]=='.' &&
    				data[strlen(data)-3] != data[strlen(data)-1]

第四题 机器人塔（47分）

X星球的机器人表演拉拉队有两种服装，A和B。
他们这次表演的是搭机器人塔。

类似：

     A
    B B
   A B A
  A A B B
 B B B A B
A B A B B A

队内的组塔规则是：

A 只能站在 AA 或 BB 的肩上。
B 只能站在 AB 或 BA 的肩上。

你的任务是帮助拉拉队计算一下，在给定A与B的人数时，可以组成多少种花样的塔。

输入一行两个整数 M 和 N，空格分开（0

要求输出一个整数，表示可以产生的花样种数。

例如：
用户输入：
1 2

程序应该输出：
3

再例如：
用户输入：
3 3

程序应该输出：
4

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

思路：DFS

1. 一旦最底下一层被确定，上面部分也就全部确定了，所以只需要枚举最底层
2. 最底层每个枚举都要检测A、B是否够用以剪掉不合格枝，优化算法
3. 每次枚举完最底层都尝试填完整个金字塔，一旦A、B数量不足则返回0，否则返回1
4. 累加所有能够完整填完整个金字塔的组合数

• 一旦数据规模接近M=500，N=500时，最底层大约长45个位置，即枚举2^45约等于35亿亿的规模，这必定是超时的，但是对于问题规模较小时可以拿到一点分数

代码实现

#include
#include
using namespace std;

int N,M,A,B;

//检查最底层是否有足够的AB可填,1代表A，0代表B 
bool check(long long num,int record[],int len){
     
	int t;
	for(int i=len-1;i>=0;i--){
     
		t=num%2;
		t==1?A--:B--;
		if(A<0||B<0) return false; 
		record[i]=t;
		num=num>>1;
		//num*=2;
	}
	return true;
}

//填充record记录表 
long long fill_record(int **record,int len){
     
	int t;
	for(int i=len-1;i>=0;i--){
     
		for(int j=0;j<=i;j++){
     
			t=record[i+1][j]==record[i+1][j+1]?1:0;
			t==1?A--:B--;
			if(A<0||B<0) return 0;
			record[i][j]=t; 
		}
	}
	return 1;
}

int main(){
     
	cin>>M>>N;
	int len=0,count=0,sum=M+N;
	long long max=1,ans=0;
	while(count<sum){
     
		len++;
		count+=len;
	}
	if(count!=sum){
     
		cout<<0;
		return 0;
	}
	for(int i=0;i<len;i++) max=max<<1;
	int **record=new int*[len];
	for(int i=0;i<len;i++)	record[i] = new int [i+1];
	for(long long i=0;i<max;i++){
     		//枚举所有组合
		A=M;							//记录剩余的A个数
		B=N;							//记录剩余的B个数
		if(check(i,record[len-1],len)){
     	//填最底下一层，如果能填满返回true，否则返回false
			ans+=fill_record(record,len-1);
		}
	}
	cout<<ans;
	for(int i=0;i<len;i++)	delete record[i];
	delete record;
	//cout<
	return 0; 
} 

优化一：利用记事本和回溯

1. 当规模最大时（M=499，N=499）时，金字塔最底层长度len=45,申请一个底长为45的金字塔数组

2. 输入M，N计算出len

3. 深度优先遍历从左下角开始填充底长len的金字塔，每层自下向上填充，方向如下

4. 每填充完一层记录当前金字塔含A、B的个数i，j利用记事本数组record累加（i，j）组合可变化的数量

5. 每次填充完计算i，j，一旦i>M或者j>N直接停止往下遍历（剪枝）以优化算法

6. 遍历完所有组合以后记事本记录了所有的规模为i，j时的可组合个数

7. 查表record[M] [N]就得到答案

• 优化点：用1表示A，-1表示B，A和B通过乘以-1可以实现转化，方法是自顶向下，先假定第一行为1或者-1，然后针对这两种情况展开到所有可能，选择其中满足输入A，B个数要求的可能。整个过程只使用到递归，一行一行地得到结果。

优化一实现

#include
#include
#include
#define MAX 500
#define MAXLEN 45
using namespace std;

int LEN=0;
int M,N;
int record[MAX][MAX];
int **tower;

//完成record和tower的初始化工作 
void init(){
     
	for(int i=0;i<MAX;i++)
		for(int j=0;j<MAX;j++)
			record[i][j]=0;
	tower = new int*[MAXLEN];
	for(int i=0;i<MAXLEN;i++)
		tower[i] = new int[i+1];
}

void finish(){
     
	for(int i=0;i<LEN;i++)
		delete tower[i];
	delete tower;	
}

void dfs(int len,int sign,int m,int n){
     
	if(len==LEN){
     
		return;		//45层填完
	}
	int t=LEN-1;
	if(sign){
     					//当前最底下位置尝试填B 
		for(int i=len;i>=0;i--,t--)	
			tower[t][i]=-tower[t][i];	//填充该层金字塔最右上层 
	}else{
     						//当前最底下位置尝试填A 
		tower[t--][len]=1;		//1表示A，-1表示B 
		for(int i=len-1;i>=0;i--,t--)
			tower[t][i]=tower[t+1][i+1]==tower[t+1][i]?1:-1; 
	} 
	t=LEN-1;
	for(int i=len;i>=0;i--,t--)	//统计该层A的个数 
		if(tower[t][i]==1) m++;
		else n++;
	if(m>M||n>N)
		return;
	record[m][n]++;
	dfs(len+1,0,m,n);
	return dfs(len+1,1,m,n);
}

int main(){
     
	init();
	cin>>M>>N;
	int count=0,sum=M+N;
	while(count<sum){
     
		LEN++;
		count+=LEN;
	}
	dfs(0,0,0,0);
	dfs(0,1,0,0);
	cout<<record[M][N];
	finish();
	return 0;
} 

优化二：硬编码

• 对优化一的代码加一改造，可以发现当给出数据计算出的LEN大于20时，计算就会超时了，也就是说小于50%的数据都是超时的。

• 测试用时代码如下

  #include
  #include
  #include
  #define MAX 500
  #define MAXLEN 45
  using namespace std;
  
  int LEN=0;
  int M,N;
  int record[MAX][MAX];
  int **tower;
  
  //完成record和tower的初始化工作 
  void init(){
         
  	for(int i=0;i<MAX;i++)
  		for(int j=0;j<MAX;j++)
  			record[i][j]=0;
  	tower = new int*[MAXLEN];
  	for(int i=0;i<MAXLEN;i++)
  		tower[i] = new int[i+1];
  }
  
  void finish(){
         
  	for(int i=0;i<LEN;i++)
  		delete tower[i];
  	delete tower;	
  }
  
  void dfs(int len,int sign,int m,int n){
         
  	if(len==LEN){
         
  		return;		//LEN层填完
  	}
  	int t=LEN-1;
  	if(sign){
         					//当前最底下位置尝试填B 
  		for(int i=len;i>=0;i--,t--)	
  			tower[t][i]=-tower[t][i];	//填充该层金字塔最右上层 
  	}else{
         						//当前最底下位置尝试填A 
  		tower[t--][len]=1;		//1表示A，-1表示B 
  		for(int i=len-1;i>=0;i--,t--)
  			tower[t][i]=tower[t+1][i+1]==tower[t+1][i]?1:-1; 
  	} 
  	t=LEN-1;
  	for(int i=len;i>=0;i--,t--)	//统计该层A的个数 
  		if(tower[t][i]==1) m++;
  		else n++;
  	if(m>=MAX||n>=MAX)
  		return;
  	record[m][n]++;
  	dfs(len+1,0,m,n);
  	return dfs(len+1,1,m,n);
  }
  
  int main(){
         
  	init();
  	clock_t start,end; 
  	for(LEN=10;LEN<30;LEN++){
         
  		start=clock();
  		dfs(0,0,0,0);
  		dfs(0,1,0,0);
  		end=clock();
  		cout<<"LEN="<<LEN<<"时初始化用时："<<end-start<<"ms"<<endl; 	
  	}
  	finish();
  	return 0;
  } 
  

  

• 既然这个程序最终目的是填满record数组后查表就可以得到结果，可以将数组所有值输出到文件中，然后硬编码写入数组，减去了大量的计算时间而只需要查表的时间就能得到结果。

• 按照上图的时间估算LEN=30时填表需要的时间约20分钟左右，对于4个小时的比赛时间完全是可接受的，而直接计算最大规模的LEN=45时填表时间超过4个小时，是完全不可能在比赛时间内得出结果的。故该方法可以提高分数，但是不能得到满分。出于运行时间考虑填写LEN=30时的表格，得分范围从LEN=20提升到了LEN=30。

• 获取LEN=30数组代码如下

  #include
  #include
  #include
  #define MAX 500
  #define MAXLEN 45
  using namespace std;
  
  int LEN=30;
  int M,N;
  int record[MAX][MAX];
  int **tower;
  
  //完成record和tower的初始化工作 
  void init(){
         
  	for(int i=0;i<MAX;i++)
  		for(int j=0;j<MAX;j++)
  			record[i][j]=0;
  	tower = new int*[MAXLEN];
  	for(int i=0;i<MAXLEN;i++)
  		tower[i] = new int[i+1];
  }
  
  void finish(){
         
  	for(int i=0;i<LEN;i++)
  		delete tower[i];
  	delete tower;	
  }
  
  void dfs(int len,int sign,int m,int n){
         
  	if(len==LEN){
         
  		return;		//45层填完
  	}
  	int t=LEN-1;
  	if(sign){
         					//当前最底下位置尝试填B 
  		for(int i=len;i>=0;i--,t--)	
  			tower[t][i]=-tower[t][i];	//填充该层金字塔最右上层 
  	}else{
         						//当前最底下位置尝试填A 
  		tower[t--][len]=1;		//1表示A，-1表示B 
  		for(int i=len-1;i>=0;i--,t--)
  			tower[t][i]=tower[t+1][i+1]==tower[t+1][i]?1:-1; 
  	} 
  	t=LEN-1;
  	for(int i=len;i>=0;i--,t--)	//统计该层A的个数 
  		if(tower[t][i]==1) m++;
  		else n++;
  	if(m>=MAX||n>=MAX)
  		return;
  	record[m][n]++;
  	dfs(len+1,0,m,n);
  	return dfs(len+1,1,m,n);
  }
  
  int main(){
         
  	init();
  	dfs(0,0,0,0);
  	dfs(0,1,0,0);
  	FILE *fp=fopen("运算结果.txt","w"); 
  	fprintf(fp,"{");
  	for(int i=0;i<MAX;i++){
         
  		fprintf(fp,"{");
  		for(int j=0;j<MAX;j++){
         
  			fprintf(fp,"%d",record[i][j]);
  			if(j!=MAX-1) fprintf(fp,",");
  		}
  		fprintf(fp,"}");
  		if(i!=MAX-1) fprintf(fp,",\n");
  	}
  	fprintf(fp,"}");
  	fclose(fp);
  	finish();
  	return 0;
  } 
  

• 运行得到文件夹，将文件夹中的内容复制到数组中，直接硬编码，接收到M，N后直接输出record[M] [N]就得到结果了，时间复杂度是O（1）

• 上面的方法可以得到所有LEN<=30的正确输出，但是对于LEN>30，但是M或者N极小的情况，通过剪枝也可以快速得到结果

• 由以上分析得出优化二算法：以硬编码为基础，将LEN<=30的所有结果硬编码到程序中，对于小于这个范围的M,N直接查表，对于大于这个规模的数据，采用DFS+剪枝算法尽可能计算更多的结果

优化二实现

#include
#define MAX 500
#define MAXLEN 45
using namespace std;

int M,N,LEN=0,result=0;
int **tower;
int record[MAX][MAX]={
     {
     ..},{
     ..},...};	//将LEN<=30的结果数组拷到这里，能快速完成计算，这里不复制了

//完成record和tower的初始化工作 
void init(){
     
	for(int i=0;i<MAX;i++)
		for(int j=0;j<MAX;j++)
			record[i][j]=0;
	tower = new int*[MAXLEN];
	for(int i=0;i<MAXLEN;i++)
		tower[i] = new int[i+1];
}

//销毁金字塔的内存 
void finish(){
     
	for(int i=0;i<LEN;i++)
		delete tower[i];
	delete tower;	
}

void dfs(int len,int sign,int m,int n){
     
	if(len==LEN) return;		//LEN层填完
	int t=LEN-1;
	if(sign){
     					//当前最底下位置尝试填B 
		for(int i=len;i>=0;i--,t--)	
			tower[t][i]=-tower[t][i];	//填充该层金字塔最右上层 
	}else{
     						//当前最底下位置尝试填A 
		tower[t--][len]=1;		//1表示A，-1表示B 
		for(int i=len-1;i>=0;i--,t--)
			tower[t][i]=tower[t+1][i+1]==tower[t+1][i]?1:-1; 
	} 
	t=LEN-1;
	for(int i=len;i>=0;i--,t--)	//统计该层A的个数 
		tower[t][i]==1?m++:n++;
	if(m>M||n>N) return;
	record[m][n]++;
	dfs(len+1,0,m,n);
	return dfs(len+1,1,m,n);
}

int main(){
     
	cin>>M>>N;
	int count=0,sum=M+N;
	while(count<sum){
     
		LEN++;
		count+=LEN;
	}
	if(count!=count){
     
		cout<<0;
		return 0;
	}
	if(LEN<=30){
     
		cout<<record[M][N];
		return 0;
	}
	init();
	dfs(0,0,0,0);
	dfs(0,1,0,0);
	cout<<record[M][N];
	finish();
	return 0; 
}

• 运行测试

  • LEN=30时瞬间出答案
    
  • ​ LEN>30，N较小时也能快速得出答案
    

第五题 广场舞（77分）

LQ市的市民广场是一个多边形，广场上铺满了大理石的地板砖。

地板砖铺得方方正正，就像坐标轴纸一样。
以某四块砖相接的点为原点，地板砖的两条边为两个正方向，一块砖的边长为横纵坐标的单位长度，则所有横纵坐标都为整数的点都是四块砖的交点（如果在广场内）。

广场的砖单调无趣，却给跳广场舞的市民们提供了绝佳的参照物。每天傍晚，都会有大批市民前来跳舞。
舞者每次都会选一块完整的砖来跳舞，两个人不会选择同一块砖，如果一块砖在广场边上导致缺角或者边不完整，则没人会选这块砖。
（广场形状的例子参考【图1.png】）

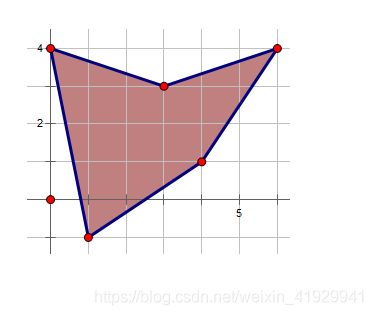
现在，告诉你广场的形状，请帮LQ市的市长计算一下，同一时刻最多有多少市民可以在广场跳舞。

【输入格式】
输入的第一行包含一个整数n，表示广场是n边形的（因此有n个顶点）。
接下来n行，每行两个整数，依次表示n边形每个顶点的坐标（也就是说广场边缘拐弯的地方都在砖的顶角上。数据保证广场是一个简单多边形。

【输出格式】
输出一个整数，表示最多有多少市民可以在广场跳舞。

【样例输入】
5
3 3
6 4
4 1
1 -1
0 4

【样例输出】
7

【样例说明】
广场如图1.png所示，一共有7块完整的地板砖，因此最多能有7位市民一起跳舞。

【数据规模与约定】
对于30%的数据，n不超过100，横纵坐标的绝对值均不超过100。
对于50%的数据，n不超过1000，横纵坐标的绝对值均不超过1000。
对于100%的数据，n不超过1000，横纵坐标的绝对值均不超过100000000（一亿）。

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

思路：以点代面

1. 找到所有顶点中的x的范围和y的范围，以这个矩形为范围枚举所有的点
2. 以当前枚举的点为起点做射线，如果射线与边界有奇数个交点（交点为顶点则算2个）则该点在区域内
3. 以该点为方形区域的左下顶点，若4个顶点都在区域内，则该方格在区域内
4. 统计区域内方格的个数
5. 判断一个点是否在区域内：
   • 点在刚好在顶点上，遍历所有顶点就可以判断出
   • 点刚好在边界上，该点y值刚好介于线段两个端点之间，用两点式代入该线段方程计算得到0
   • 点在区域内但不在边界上：该点做水平射线与边界有奇数个交点
   • 注意：
     • 若交点正好是端点，则需要判断的前后端点是否都在该端点的上方或都在下方，如都在上方的或下方则算2个（即0个），否则算1个
     • 若一条边是水平的，向两边延伸，若延伸后两边的顶点都在线的上方或都在下方，算2个交点（即0个），否则算1个

代码实现

#include
#include
using namespace std;

int *X,*Y,N;

//给定两个坐标点和一个Y值解出这两个坐标点确定的直线与y=Y这条直线相交的x值 
float get_x(int y,int x1,int y1,int x2,int y2){
     
	if(x1==x2) return x1;
	float x=((float)(y-y2)*(x1-x2))/(y1-y2)+x2;
	//cout<
	return x;
}

//判断点是否在范围内 
bool judge(int x,int y){
     
	//1.点刚好在端点上 
	for(int i=0;i<N;i++)
		if(x==X[i]&&y==Y[i]){
     
			//cout<<"点("<
			return true;
		}
	//2.点刚好在边界上
	for(int i=0;i<N-1;i++){
     
		if(x==X[i]||y==Y[i]||x==X[i+1]||y==Y[i+1]) continue;
		if((Y[i]-y)*(X[i]-X[i+1])==(Y[i]-Y[i+1])*(X[i]-x)){
     
			//cout<<"点("<
			return true;
		}
	}
	//3.点在区域内
	int flag=-1,j;
	int p,q;				//p是前一不同Y值下标，q是后一不同Y值下标 
	float xt;				//xt是水平射线与交点的x值
	for(int i=0;i<N;i++){
     
		j=(i+1==N?0:i+1);
		if(y==Y[i]){
     		//向右的水平射线刚好与端点相交 
			if(x>=X[i]) continue;
			p=(i==0?N-1:i-1);
			q=j; 
			if(y==Y[p]) p=(p==0?N-1:p-1);
			if(y==Y[q])	q=(q==N-1?0:q+1);
			if(Y[p]>y!=Y[q]>y) flag=-flag; 
		}else if(y>Y[i]!=y>Y[j]){
     	//水平射线与线段中间相交 
			if(y==Y[j]) continue;
			xt=get_x(y,X[i],Y[i],X[j],Y[j]);
			if(xt-x>0) flag=-flag;
		}
	}
	if(flag>0){
     
		//cout<<"点("<
		return true;	
	}
	else return false;
}

int main(){
     
	int count=0;
	//接收参数 
	cin>>N;
	X=new int[N];
	Y=new int[N];
	int minX=100000001,maxX=-100000001,minY=100000001,maxY=-100000001;
	for(int i=0;i<N;i++){
     
		cin>>X[i]>>Y[i]; 
		if(X[i]<minX) minX=X[i];
		if(X[i]>maxX) maxX=X[i];
		if(Y[i]<minY) minY=Y[i];
		if(Y[i]>maxY) maxY=Y[i];
	}
	//枚举所有点
	for(int i=minX;i<maxX;i++){
     
		for(int j=minY;j<maxY;j++){
     
			if(judge(i,j)&&judge(i+1,j)&&judge(i,j+1)&&judge(i+1,j+1)){
     
				//cout<<"("<
				count++;	
			}
		}
	} 
	cout<<count;
	return 0;
} 

优化：去冗余判断

• 找到所有范围内的点的集合，再判断每个点代表的方格的4个点是否都在这个集合内，如果都在，则这个方格是在范围内的

第六题 生成树计数（99分）

给定一个 n×m 的格点图，包含 n 行 m 列共 n×m 个顶点，相邻的顶点之间有一条边。
【图1.png】给出了一个3×4的格点图的例子。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wL9wj8gZ-1605268069397)(C:\Users\Mr.航\Desktop\蓝桥杯\决赛\第七届蓝桥杯大赛个人赛（软件类）决赛真题\C语言B组\6\图1.png)]

如果在图中删除部分顶点和其相邻的边，如上图删除第2行第3列和第3行第1列的顶点后，如【图2.png】所示。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ombfUQGf-1605268069399)(C:\Users\Mr.航\Desktop\蓝桥杯\决赛\第七届蓝桥杯大赛个人赛（软件类）决赛真题\C语言B组\6\图2.png)]

图的生成树指包含图中的所有顶点和其中的一部分边，使得任意两个顶点之间都有由边构成的唯一路径。如果两个生成树包含有不同的边即被认为不同，则上图中共有31种不同的生成树，其中a边不选有10种，a边选有21种。
给出格点图中保留的顶点的信息，请计算该图一共有多少种不同的生成树。

【输入格式】
输入的第一行包含两个整数n, m，用空格分隔，表示格点图的行数和列数。
接下来n行，每行m个字母（中间没有分隔字符），每个字母必然是大写E或大写N，E表示对应的顶点存在，N表示对应的顶点不存在。保证存在至少一个顶点。

【输出格式】
输出一行，包含一个整数，表示生成树的个数。答案可能很大，你只需要计算答案除以1000000007的余数即可。

【样例输入】
3 4
EEEE
EENE
NEEE

【样例输出】
31

【数据规模与约定】
对于10%的数据，1<=n<=2。
对于30%的数据，1<=n<=3。
对于40%的数据，1<=n<=4。
对于50%的数据，1<=n<=5。
另有20%的数据，1<=n*m<=12。
另有10%的数据，1<=m<=15。
对于100%的数据，1<=n<=6，1<=m<=100000。

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 4500ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。