栈、队列、链表等数据结构,都是顺序数据结构。而树是非顺序数据结构。树型结构是一类非常重要的非线性结构。直观地,树型结构是以分支关系定义的层次结构。
- 有且仅有一个特定的称为根(Root)的结点;
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,T3,...Tm,其中每一个集合本身又是一棵树,并且称为根的子树(Subtree)。
二叉树
二叉树(Binary Tree)是另一种树型结构,它的特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分(其次序不能任意颠倒。)
二叉树的性质
- 在二叉树的第 i 层上至多有个结点(i>=1)。
- 深度为k的二叉树至多有 - 1 个结点,(k>=1)。
- 对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
- 一棵深度为k且有 - 1个结点的二叉树称为满二叉树。
- 深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树。
完全二叉树的两个特性
- 具有n个结点的完全二叉树的深度为 + 1。
- 如果对一棵有n个结点的完全二叉树(其深度为 + 1)的结点按层序编号(从第1层到第 + 1,每层从左到右),则对任一结点(1<=i<=n)有
如果 i = 1,则结点 i 是二叉树的根,无双亲;如果i > 1,则其双亲parent(i)是结点 Math.floor(i/2)。
如果 2i > n,则结点 i 无左孩子(结点i为叶子结点);否则其左孩子LChild(i) 是结点 2i。
如果 2i + 1 > n,则结点 i 无右孩子;否则其右孩子 RChild(i) 是结点 2i + 1。
二叉树的遍历
遍历二叉树(Traversing Binary Tree):是指按指定的规律对二叉树中的每个结点访问一次且仅访问一次。
二叉树有深度遍历和广度遍历, 深度遍历有前序、 中序和后序三种遍历方法。二叉树的前序遍历可以用来显示目录结构等;中序遍历可以实现表达式树,在编译器底层很有用;后序遍历可以用来实现计算目录内的文件及其信息等。
前序遍历:访问根–>遍历左子树–>遍历右子树。
中序遍历:遍历左子树–>访问根–>遍历右子树。
后序遍历:遍历左子树–>遍历右子树–>访问根。
广度遍历:按照层次一层层遍历。
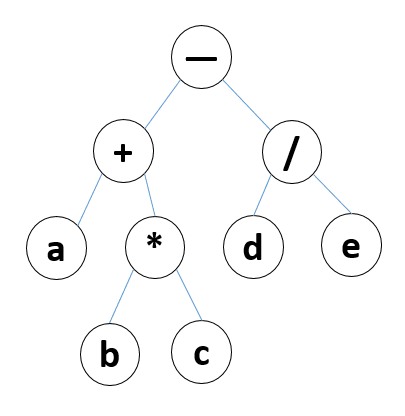
例如(a+b*c)-d/e,该表达式用二叉树表示如图:
js中的二叉树
上述二叉树(a+b*c)-d/e在js中可以用对象的形式表示出来:
const tree = {
value: "-",
left: {
value: '+',
left: {
value: 'a',
},
right: {
value: '*',
left: {
value: 'b',
},
right: {
value: 'c',
}
}
},
right: {
value: '/',
left: {
value: 'd',
},
right: {
value: 'e',
}
}
}
先序遍历: ["-", "+", "a", "*", "b", "c", "/", "d", "e"]
- 递归版本
- 先遍历根节点,将值存入数组,然后递归遍历:先左节点,将值存入数组,继续向下遍历,直到二叉树为空,则遍历结束;
- 然后再回溯遍历右节点,将值存入数组,这样递归循环,直到子树为空,则遍历结束。
let result = []
let dfs = function (node) {
if (node) {
result.push(node.value)
dfs(node.left)
dfs(node.right)
}
return result
}
console.log(dfs(tree))
- 非递归版本
- 先序非递归遍历是利用了栈,将根结点放入栈中,然后再取出来,将值放入结果数组;
- 然后如果存在右子树,将右子树压入栈;
- 如果存在左子树,将左子树压入栈;
- 然后循环判断栈是否为空,重复上述步骤。
let dfs = function (nodes) {
let result = []
let stack = []
stack.push(nodes)
while (stack.length) { // 等同于 while(stack.length !== 0) 直到栈中的数据为空
let node = stack.pop() // 这其实树或者节点
result.push(node.value) // 取到现在的节点的value值
if (node.right) stack.push(node.right) // 先压入右子树
if (node.left) stack.push(node.left) // 后压入左子树,这样push()先出
}
return result
}
console.log(dfs(tree)) // ["-", "+", "a", "*", "b", "c", "/", "d", "e"]
中序遍历:["a", "+", "b", "*", "c", "-", "d", "/", "e"]
- 递归版本
先递归遍历左子树,从最左的一个左子树存入数组;然后回溯遍历双亲结点,再是右子树,这样递归循环。
let result = []
let dfs = function (node) {
if (node) {
dfs(node.left)
result.push(node.value)
dfs(node.right)
}
}
- 非递归遍历
将当前结点压入栈,然后将左子树当做当前结点,如果当前结点为空,将双亲结点取出来,将值保存进数组,然后将右子树当做当前结点,进行循环。
let dfs = function (node) {
let result = []
let stack = []
while (stack.length || node) {
if(node) {
stack.push(node)
node = node.left
} else {
node = stack.pop()
result.push(node.value)
node = node.right
}
}
return result
}
console.log(dfs(tree))
后序遍历:["a", "b", "c", "*", "+", "d", "e", "/", "-"]
- 递归遍历
先走左子树,当左子树没有孩子结点时,将此结点的值放入数组中,然后回溯遍历双亲结点的右结点,递归遍历。
let result = []
function dfs (node) {
if(node) {
dfs(node.left)
dfs(node.right)
result.push(node.value)
}
}
-
非递归版本
- 初始化一个栈,将根节点压入栈中,并标记为当前节点(node);
- 当栈为非空时,执行步骤3,否则执行结束;
- 如果当前节点(node)有左子树且没有被 touched,则执行4;如果当前结点有右子树,被 touched left 但没有被 touched right 则执行5 否则执行6;
- 对当前节点(node)标记 touched left,将当前节点的左子树赋值给当前节点(node=node.left) 并将当前节点(node)压入栈中,回到3;
- 对当前节点(node)标记 touched right,将当前节点的右子树赋值给当前节点(node=node.right) 并将当前节点(node)压入栈中,回到3;
- 清理当前节点(node)的 touched 标记,弹出栈中的一个节点并访问,然后再将栈顶节点标记为当前节点(item),回到3。
function dfs(node) {
let result = []
let stack = []
stack.push(node)
while(stack.length) {
// 不能用node.touched !== 'left' 标记‘left’做判断,
// 因为回溯到该结点时,遍历右子树已经完成,该结点标记被更改为‘right’ 若用标记‘left’判断该if语句会一直生效导致死循环
if(node.left && !node.touched) { // 不要写成if(node.left && node.touched !== 'left')
// 遍历结点左子树时,对该结点做 ‘left’标记;为了子结点回溯到该(双亲)结点时,便不再访问左子树
node.touched = 'left'
node = node.left
stack.push(node)
continue
}
if(node.right && node.touched !== 'right') { // 右子树同上
node.touched = 'right'
node = node.right
stack.push(node)
continue
}
node = stack.pop() // 该结点无左右子树时,从栈中取出一个结点,访问(并清理标记)
node.touched && delete node.touched // 可以不清理不影响结果 只是第二次对同一颗树再执行该后序遍历方法时,结果就会出错啦因为你对这棵树做的标记还留在这棵树上
result.push(node.value)
node = stack.length ? stack[stack.length - 1] : null
//node = stack.pop() 这时当前结点不再从栈中取(弹出),而是不改变栈数据直接访问栈中最后一个结点
//如果这时当前结点去栈中取(弹出)会导致回溯时当该结点左右子树都被标记过时 当前结点又变成从栈中取会漏掉对结点的访问(存入结果数组中)
}
return result // 返回值
}
js中二叉树的广度遍历
- 递归版本
广度优先遍历二叉树(层序遍历)是用队列来实现的,广度遍历是从二叉树的根结点开始,自上而下逐层遍历;在同一层中,按照从左到右的顺序对结点逐一访问。
// 广度优先遍历
let result = []
let stack = [tree]
let count = 0
let bfs = function() {
let node = stack[count] // 当前节点
result.push(node.value)
if(node.left) stack.push(node.left)
if(node.right) stack.push(node.right)
count++ // 取到下一个节点
bfs()
}
- 非递归版本
function bfs(node) {
let result = []
let queue = []
queue.push(node)
let pointer = 0
while (pointer < queue.length) {
let node = queue[pointer++]
result.push(node.value)
if(node.left) queue.push(node.left)
if(node.right) queue.push(node.right)
}
return result
}
参考文章
js 中二叉树的深度遍历与广度遍历(递归实现与非递归实现)
二叉树与JavaScript