深度优先搜索(DFS)与广度优先搜索(BFS)详解
深度优先搜索(DFS)和宽度优先搜索(BFS)都是常见的搜索算法。在学习DFS和BFS之前,我们首先得知道递归函数的概念。
1. 递归函数
通俗地讲,一个函数自己调用自己的行为就叫递归,该函数就叫递归函数。如计算一个数的阶乘,就可以利用递归来实现。
我们知道一个数的阶乘可以等于这个数乘上这个数减1的阶乘,如 3 ! = 3 × 2 ! 3!=3\times2! 3!=3×2!,便有递推式:
n ! = n × ( n − 1 ) ! n!=n\times(n-1)! n!=n×(n−1)!
规定 0 ! = 1 0!=1 0!=1,便可以很容易地编写出如下函数:
int f(int n) {
if (n == 0) {
return 1;
}
return n * f(n-1);
}
递归函数必须要有循环退出的条件,在这段代码中, n = = 0 n==0 n==0就是循环退出的条件。如果没有循环退出的条件,那么函数就会无限地调用下去,导致程序崩溃。
下面是计算阶乘的递归过程:
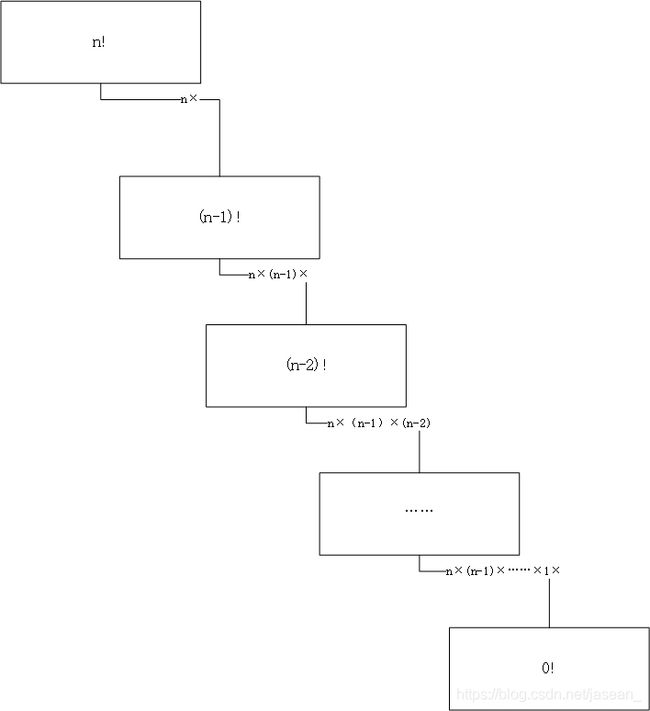
类似地,我们可以试着编写计算斐波那契数列的某一项的递归函数。斐波那契数列的定义如下:
设数列 { a n } , \{a_n\}, { an},若满足 a 0 = 0 a_0=0 a0=0, a 1 = 1 a_1=1 a1=1, a n = a n − 1 + a n − 2 ( n ≥ 2 ) a_n=a_{n-1}+a_{n-2}(n\geq2) an=an−1+an−2(n≥2),则称数列 { a n } \{a_n\} { an}为斐波那契数列
根据定义,我们知道斐波那契数列的递推式为 a n = a n − 1 + a n − 2 a_n=a_{n-1}+a_{n-2} an=an−1+an−2,循环退出的条件为 n = 0 n=0 n=0或 n = 1 n=1 n=1,这样就可以很容易地写出该递归函数:
int fib(int n) {
if (n <= 1) {
return n;
}
return fib(n-1) + fib(n-2);
}
我们在使用这个函数时,即使是求 n = 40 n=40 n=40这样 n n n较小的情况的时候,也需要花费很长的时间。这是因为该递归函数在进行递归时,一次递归同时调用了两次自身,这样时间上就会随着 n n n的增大指数级增加,如当 n = 5 n=5 n=5时:
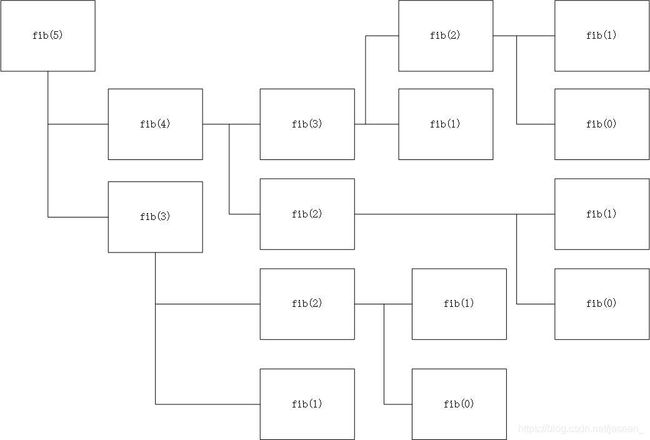
可以看到有很多重复、不必要的调用,如fib(2)在程序中被调用了3次,这就浪费了时间,因此我们可以使用一个数组来将每一次计算得到的数存储起来,如果这一项被计算过了,直接返回数组对应的元素即可:
#include 2. 深度优先搜索
深度优先搜索(DFS,Depth-First Search)是搜索算法的一种,它从某一个状态开始,不断地转移状态直到无法转移,然后回退到前一步的状态,继续转移到其他状态,如此不断重复,直到找到最终的解。我们先来看一下深度优先搜索的搜索树:
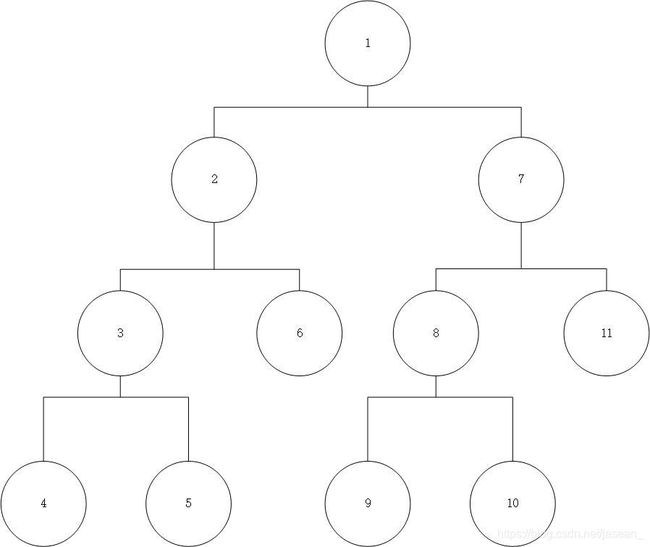
从这个搜索树中可以看出,DFS是从根节点出发,每次遍历它的第一个孩子节点,当遍历到叶子节点时候,回退一步返回到它的父亲节点,接着遍历父亲节点的其它孩子节点。如此重复,直到遍历完所有节点。
我们来试着解一下部分和问题:
部分和问题:
给定整数 a 1 a_1 a1, a 2 a_2 a2, … \dots …, a n a_n an,判断是否可以从中选出若干数,使得它们的和恰好等于 k k k。
第一行输入一个整数 n n n,表示有几个数据
第二行输入 n n n个整数,表示 a i a_i ai
第三行输入一个整数,表示 k k k
限制条件:
* 1 ≤ n ≤ 20 1\leq n \leq 20 1≤n≤20
* − 1 0 8 ≤ a i ≤ 1 0 8 -10^8 \leq a_i \leq 10^8 −108≤ai≤108
* − 1 0 8 ≤ k ≤ 1 0 8 -10^8 \leq k \leq 10^8 −108≤k≤108
样例输入1:
4
1 2 4 7
13
样例输出2:
Yes
样例输入2:
4
1 2 4 7
15
样例输出:
No
分析:
按照DFS的思想,我们可以把 a 1 a_1 a1作为搜索树的根节点,左子树为 a 1 a_1 a1被选用的情况,右子树为 a 1 a_1 a1不被选用的情况,用一个变量sum来计算被选择数据的和。

#include 接着我们来提高一下难度:
Lakee Counting(POJ NO.2386):
有一个大小为 N × M N\times M N×M的园子,雨后积起了水,八连通的积水被认为是连接在一起的,请求出园子里共有多少个水洼。(八连通指的是下图中相对 w w w的 ∗ * ∗的部分)
∗ ∗ ∗ *** ∗∗∗
∗ w ∗ *w* ∗w∗
∗ ∗ ∗ *** ∗∗∗
第一行输入一个整数 N N N
第二行输入一个整数 M M M
接下来的 N N N行 M M M列表示园子的范围,其中“ w w w”为积水
限制条件:
* N , M ≤ 100 N,M \leq 100 N,M≤100
样例输入:
w . . . . . . . . w w . w........ww. w........ww.
. w w w . . . . . w w w .www.....www .www.....www
. . . . w w . . . w w . ....ww...ww. ....ww...ww.
. . . . . . . . . w w . .........ww. .........ww.
. . . . . . . . . w . . .........w.. .........w..
. . w . . . . . . w . . ..w......w.. ..w......w..
. w . w . . . . . w w . .w.w.....ww. .w.w.....ww.
w . w . w . . . . . w . w.w.w.....w. w.w.w.....w.
. w . w . . . . . . w . .w.w......w. .w.w......w.
. . w . . . . . . . w . ..w.......w. ..w.......w.
样例输出:
3
分析:
可以从任意一个 w w w的位置入手,将这个位置用"."代替,并搜索它所对应八连通的位置,如果搜索的位置在园子内,并且值为 w w w,则递归调用自身,重复上述步骤;直到某个点的八连通位置内没有 w w w时退出循环。
依次对园子内的每个点进行如上操作,则dfs被调用的次数即为水洼的个数。
#include 3. 宽度优先优先搜索
宽度优先搜索(BFS,Breath-First Search)又称广度优先搜索,也是搜索算法的一种,它与深度优先搜索类似,从某个状态出发,搜索所有可恶意到达的状态。
与深度优先搜索的不同之处在于搜索的顺序,我们来看一下宽度优先搜索的搜索树:

可以看出宽度优先是先遍历根节点的所有孩子节点,再依次遍历每一个孩子节点的孩子节点。
其实深度优先搜索(DFS)隐式地利用了栈进行计算,而宽度优先搜索(BFS)利用了队列。搜索时首先将初始状态添加到队列里,然后从队列的最顶端不断取出状态,把从该状态可以转移到的状态中尚未访问过的部分加入队列;如此往复,直到队列为空或找到问题的解。深度优先搜索相当于对搜索树进行前序遍历,而宽度优先搜索则相当于层序遍历。
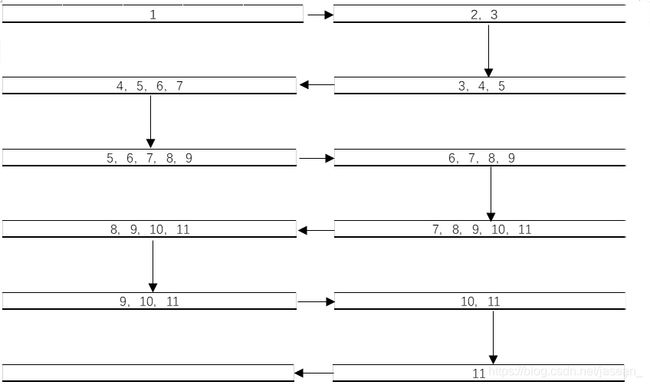
接下来我们来看一道经典的迷宫问题:
迷宫的最短路径:
给定一个大小为 N × M N\times M N×M的迷宫。迷宫由通道和墙壁组成,每一步可以向邻接的上下左右四格的通道移动。请求出从起点到终点所需的最小步数。请注意,本题假定从起点一定可以移动到终点。
第一行输入一个整数 N N N
第二行输入一个整数 M M M
接下来的 N N N行 M M M列为迷宫矩阵,“#”表示墙壁,“.”表示通道,“S”表示起点,“G”表示终点
限制条件:
N , M ≤ 100 N,M \leq 100 N,M≤100
样例输入:
10
10
# S # # # # # # . # \#S\#\#\#\#\#\#.\# #S######.#
. . . . . . # . . # ......\#..\# ......#..#
. # . # # . # # . # \#.\#\#.\#\#.\# #.##.##.#
. # . . . . . . . . .\#........ .#........
# # . # # . # # # # \#\#.\#\#.\#\#\#\# ##.##.####
. . . . # . . . . # ....\#....\# ....#....#
. # # # # # # # . # .\#\#\#\#\#\#\#.\# .#######.#
. . . . # . . . . . ....\#..... ....#.....
. # # # # . # # # . .\#\#\#\#.\#\#\#. .####.###.
. . . . # . . . G # ....\#...G\# ....#...G#
样例输出:
22
宽度优先搜索按照距开始状态由近及远的顺序进行搜索,因此可以很容易地用来求最短路径、最少操作之类的问题的答案。这个问题中,状态仅仅是目前所在位置的坐标。因此可以构造pair或者编码成int来来表达状态。当状态更加复杂时,就需要封装成一个类来表示状态了。转移的方式为四方向移动,状态数与迷宫的大小是相等的,所以复杂度为 O ( 4 × N × M ) = O ( N × M ) O(4\times N\times M)=O(N\times M) O(4×N×M)=O(N×M)。
只要将已经访问过的状态用标记管理起来,就可以很好地做到由近及远的搜索,这个问题要求最短距离,不妨用数组 d [ N ] [ N ] d[N][N] d[N][N]来把最短距离保存起来,初始时用一个充分大的常数 I N F INF INF来进行初始化,这样就保证了尚未到达的位置的值是 I N F INF INF,也就起到了标记的作用。
虽然到达终点时会停止搜索,可如果继续下去直到队列为空的话,就可以计算出各个位置的最短距离。此外,如果搜索到最后, d d d仍然为 I N F INF INF的话,这个位置就是无法从起点到达的。
用 d x [ 4 ] dx[4] dx[4]和 d y [ 4 ] dy[4] dy[4]两个数组来表示四个方向向量。这样通过一个循环可以实现方向的移动。
#include 运行的结果如下:
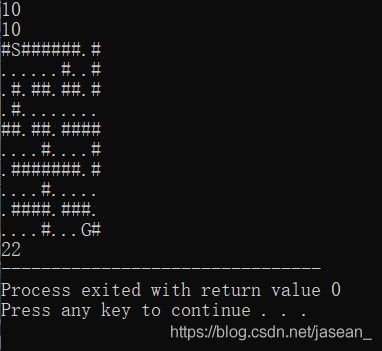
深度优先搜索和宽度优先搜索一样,都会生成所有能够遍历到的状态,因此需要对所有的状态进行处理时使用宽度优先搜索也是可以的。但是递归函数可以很简短地编写,而且状态的管理也更简单,所以大多数情况下还是用深度优先搜索实现。反之,在求取最短路时深度优先搜索需要反复经过同样的状态,所以此时还是使用宽度优先搜索为好。
宽度优先搜索会把状态逐个加入队列,因此通常需要与状态数成正比的内存空间。反之,深度优先搜索是与最大的递归深度成正比的。一般与状态数相比,递归的深度并不会太大,所以可以认为深度优先搜索更加节省内存。
这是博主写的第一篇博客,如有不明确的地方或者不懂的地方,欢迎在下方留言交流,博主也会继续分享算法知识