【数据结构】线性表
目录
-
- 一,线性表
-
- 1.基本概念
- 2.基本操作
-
- 【小结】
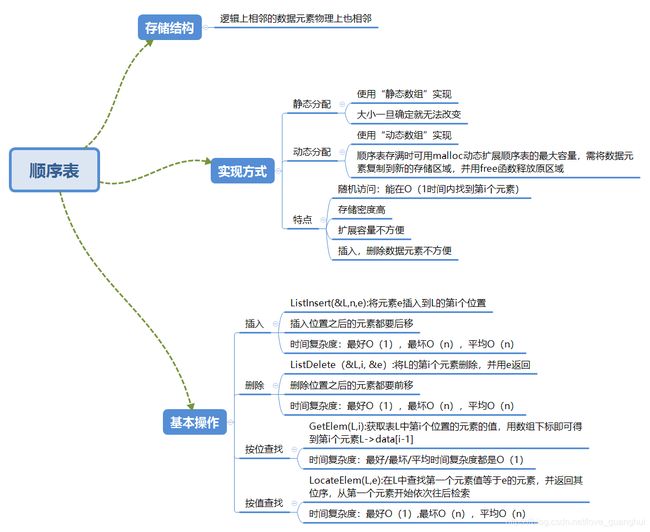
- 二,顺序表
-
- 1.存储结构
- 2.实现方式
-
- (1)静态分配
- (2)动态分配
- (3)顺序表的特点
- 3.基本操作
-
- (1) 初始化一个顺序表
- (2)销毁一个顺序表
- (3)插入元素
- (4)删除元素
- (5)按位查找
- (6)按值查找
- (7)顺序表输出
- (8)增长顺序表长度
- 【小结】
- 三,链表
-
- 1.存储结构
- 2.实现方式
-
- (1)不带头结点
- (2)带头结点
- 3.基本操作
-
- (1)插入元素
- (2)删除元素
- (3)查找元素
- (4)求表长
- (5)打印链表
- (6)建立单链表
- 【小结】
- 【总结】
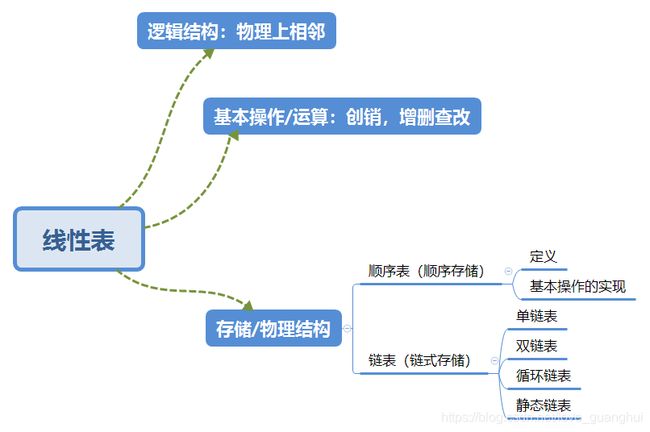
一,线性表
1.基本概念
a.定义:线性表是具有相同数据类型的n个数据元素的有限序列 ,其中n位表长,当n=0是线性表是一个空表。
b.几个概念:
·ai是线性表中的“第i个”元素线性表中的位序(注意:位序从1开始,数组下标从0开始)。
·a1是表头元素;an是表尾元素。
·除第一个元素外,每个元素有且仅有一个前驱;除最后一个元素外,每个元素有且仅有一个后继。
2.基本操作
InitList(&L):初始化表。构造一个空的线性表L,分配内存空间
DestroyList(&L):销毁操作。销毁线性表,并释放线性表L所占内存空间
ListInsert(&L,n,e):插入操作。在第n个位置插入元素e
ListDelete(&L,n,&e):删除操作。删除表L中第n个位置元素,并用e返回删除元素的值
LocateElem(&L,n):按值查找。在表L中查找指定元素n的位置
GetElem(&L,n):按位查找。获取表L中第n个位置的元素的值
其他常用操作:
Length(L):求表长。返回线性表L的长度,即元素个数
PrintList(L):输出操作。按前后顺序输出线性表L的所有值
Empty(L):判空操作。若L为空表,则返回true,否则返回false
(1)以上函数名均可自己定义,但要有可读性。
(2)有些用到&是需要保留修改的结构,这是传址运算
【小结】
二,顺序表
1.存储结构
(1)定义:顺序表是具有相同类型的n(n>=0)个数据元素的有限序列。
(2)顺序存储:在逻辑上相邻的元素存储在物理位置上也相邻的存储单元中,元素之间的关系又存储单元的邻接关系来体现。
2.实现方式
(1)静态分配
使用“静态数组”实现,在定义时就已经确定了元素的个数,且大小无法被改变。
代码实现
typedef struct SeqList
{
int data[MaxSize];//用静态的“数组”存放数据元素,“数组”的具体类型根据具体需求选择
int length;//顺序表的当前长度
}SL;//顺序表的类型定义
(2)动态分配
使用“动态数组”实现,当顺序表存满时,可再用malloc动态扩展顺序表的最大容量,需要将数据元素复制到新的存储区域,并用free函数释放原区域。
代码实现
typedef struct SeqList
{
int* data;//指向动态分配数组的指针
int MaxSize;//顺序表的最大容量
int length;//顺序表当前的长度
}SL;
(3)顺序表的特点
a.随机访问,即可以在O(1)时间内找到第i个元素。
b.存储密度高,每个节点只存储数据元素。
c.扩展内容不方便(基本采用动态分配的方式实现,扩展长度的时间复杂度也比较高)
d.插入,删除操作不方便,需要移动大量元素。
3.基本操作
研究数据结构的基本操作一般是创建,销毁,增删查改。
由于代码实现都是编者之间以int类型写的,难免出现一些问题,可能不难保证代码的健壮性,若读者发现其中的问题,可以指出
(1) 初始化一个顺序表
void InitList(SL* L)
{
L->data = (int*)malloc(InitSize * sizeof(int));//用malloc函数申请一片连续的存储空间
L->length = 0;//初始化顺序表长度为0
L->MaxSize = InitSize;
}
(2)销毁一个顺序表
void DestroyList(SL* L)
{
for (int i = 0; i < L->length; i++)//这一步可以省略
{
L->data[i] = 0;
}
L->length = 0;
}
(3)插入元素
值得注意的是,插入元素需将之后的元素从最后开始往后移,否则会出现数据覆盖的现象。
bool ListInsert(SL* L, int n, int e)//在第n个位置插入e
{
if (n > L->length + 1)//n如果超出顺序表当前长度则非法
{
return false;
}
for (int i = L->length; i >= n; i--)//从后往前依次把数据后移
{
L->data[i] = L->data[i - 1];
}
L->data[n - 1] = e;//在第n个位置插入e
L->length++;//L当前长度+1
return true;
}
(4)删除元素
而删除元素应将之后的元素从前开始前移。
bool ListDelete(SL* L, int n, int* e)//删除第n个位置的元素e
{
if (n < 0 || n > L->length + 1)
{
return false;
}
*e = L->data[n - 1];//把第n个位置的元素赋值给e
for (int i = n - 1; i < L->length; i++)
{
L->data[i] = L->data[i + 1];
}
L->length--;//顺序表当前的长度-1
return true;
}
(5)按位查找
int GetElem(SL* L, int n)//得到第n个位置的元素(按位查找)
{
return L->data[n - 1];
}
(6)按值查找
int LocateElem(SL* L, int n)//得到顺序表中值位n的元素的下标
{
for (int i = 0; i < L->length; i++)
{
if (L->data[i] == n)
{
return i;
}
}
return -1;//找不到则返回-1
}
(7)顺序表输出
void PrintList(SL* L)
{
for (int i = 0; i < L->length; i++)
{
printf("%d ", L->data[i]);
}
}
(8)增长顺序表长度
void IncreaseList(SL* L, int len)//增长顺序表的长度
{
int* p = L->data;
L->data = (int*)malloc((L->MaxSize + len) * sizeof(int));
for (int i = 0; i < L->length; i++)//将原始数据拷贝到新区域
{
L->data[i] = p[i];
}
free(p);//释放掉原来的内存空间
}
【小结】
三,链表
1.存储结构
逻辑上相邻,物理上不一定相邻。拿单链表来说,每个节点除了存放数据元素外,还要存储指向下一个节点的指针。
2.实现方式
由于作者的精力有限,以下均是单链表的实现,双链表读者可以自己参考编写。
链表的实现有两种,一种是带头节点,另一种是不带头节点,由于不带头节点的链表在写代码时不方便,故不多作分析。
(1)不带头结点
typedef struct LNode//定义一个结点
{
int data;//数据域,存放该节点的数据元素
struct LNode* next;//指针域,指向下一个结点
}Node,*LinkList;//Node表示一个结点;LinkList作为指针指向单链表
bool InitList(LinkList L)//创建一个单链表(不带头结点)
{
L = NULL;//空表,暂时还没有任何结点(防止脏数据)
return true;
}
(2)带头结点
typedef struct LNode//定义一个结点
{
int data;//数据域,存放该结点的数据元素
struct LNode* next;//指针域,指向下一个结点
}Node,*LinkList;//Node表示一个结点;LinkList作为指针指向单链表
bool InitList(LinkList L)//初始化一个单链表(带头结点)
{
//L = (Node*)malloc(sizeof(Node));//分配一个头结点,头结点不存储数据
if (L == NULL)
{
return false;//内存不足,分配失败
}
L->data = 0;
L->next = NULL;//头节点之后还没有结点
return true;
}
注意这里Node和LinkList的表达,Node(结构体类型)强调一个节点,LinkList(结构体指针类型)则强调单链表,这对于看代码,理解代码来说很重要。
3.基本操作
(1)插入元素
bool ListInsert(LinkList L, int i, int e)
{
if (i < 1)
{
return false;
}
/*if (i == 1)//对于不带头结点的单链表,插入第一个结点需要额外的操作处理
{
Node* s = (Node*)malloc(sizeof(Node));
s->data = e;
s->next = L;
L = s;//修改头指针指向新的结点,同时后续的j=1,表示当前节点是第一个结点
return true;
}*/
Node* p = L;//指针p指向当前扫描到的结点
int j = 0;//记录p当前扫描到第j个结点,虚构L头结点为第0个结点
while (p != NULL && j < i - 1)//循环找到第i-1个结点
{
p = p->next;
j++;
}
if (p == NULL)//i值不合法
{
return false;
}
//Node* s = (Node*)malloc(sizeof(Node));
//s->data = e;
//s->next = p->next;
//p->next = s;//将节点s连到p之后
//return true;//插入成功
InsertNextNode(p, e);//函数嵌套使用
}
bool InsertNextNode(Node* p, int e)//后插操作:在指定结点后插入元素e
{
Node* s = (Node*)malloc(sizeof(Node));
if (s == NULL)//内存已满,分配失败
{
return false;
}
s->data = e;
s->next = p->next;
p->next = s;
return true;
}
bool InsertPriorNode(Node* p, int e)//前插操作:在指定结点前插入元素e
{
Node* s = (Node*)malloc(sizeof(Node));
if (s == NULL)
{
return false;
}
s->data = p->data;
s->next = p->next;
p->data = e;
p->next = s;
return true;
}
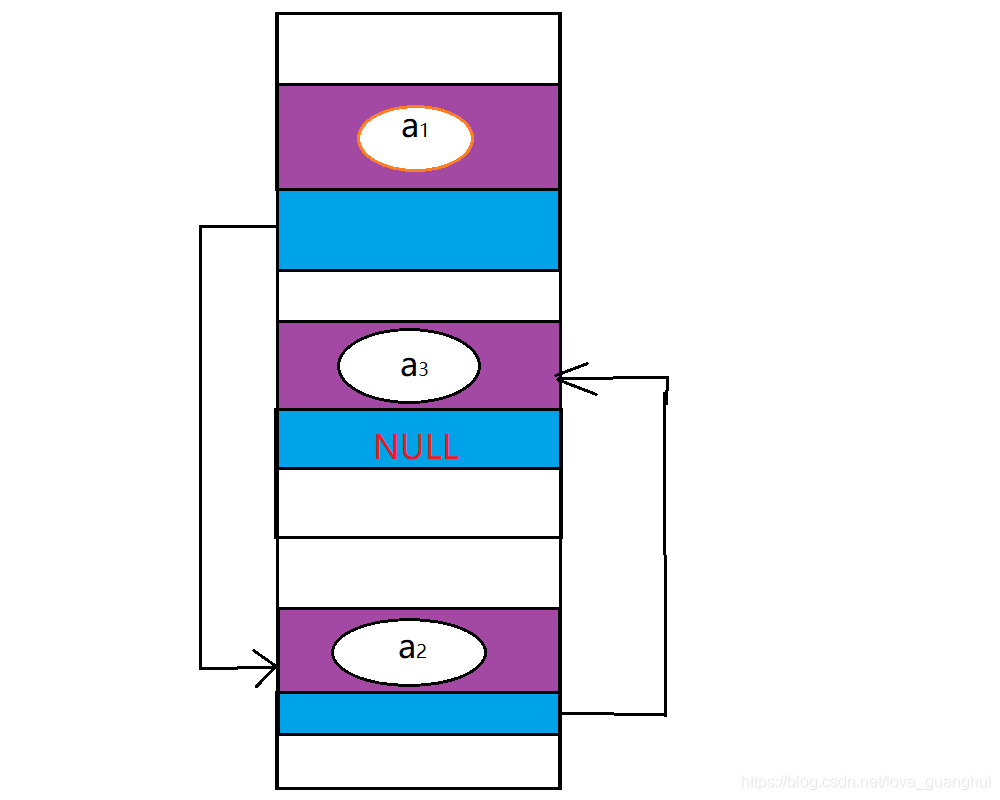
这里强调一下前插操作,由于是单链表,不能访问特定结点之前的结点,故需要创建一个指针s作为结点p的复制品,而将要插入的元素赋值给p的数据域,用一张图来理解一下
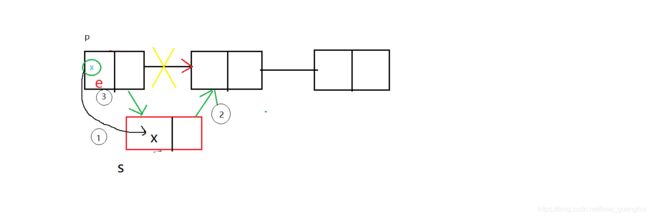
(2)删除元素
链表的删除操作相对比较容易,只需找到要删除的结点,让它前一个结点的next指针指向它后一个结点,再将这个结点的内存释放即可。
bool ListDelete(LinkList L, int i, int* e)
{
if (i < 1)
{
return false;
}
Node* p =L;
int j = 0;
while (p != NULL && j < i - 1)
{
p = p->next;
j++;
}
if (p == NULL)
{
return false;
}
//Node* q = (Node*)malloc(sizeof(Node));
//q = p->next;//q指向要删除的结点
//*e = q->data;
//p->next = q->next;
//free(q);
//return true;
DeleteNode(p);
}
bool DeleteNode(Node* p)//删除指定结点p
{
if (p == NULL)
{
return false;
}
Node* q = p->next;
p->data = q->data;//局限性:不能删除尾结点,p为最后一个结点时,q为NULL
p->next = q->next;
free(q);
return true;
}
同样对于删除特定结点p时,需要将p后的结点拷贝到p上,再释放p后一个结点,这是单链表的局限性,且无法对链表最后一个元素进行操作。
(3)查找元素
返回所找到的第一个结点
a.按位查找
Node* GetElem(LinkList L, int i)//按位查找
{
if (i < 0)
{
return NULL;
}
Node* p = L;
int j = 0;
while (L != NULL && j < i)//循环找到第i个结点
{
p = p->next;
j++;
}
return p;
}
b.按值查找
Node* LocateNode(LinkList L, int e)//按值查找
{
Node* p = L->next;
while (p->data != e && p != NULL)
{
p = p->next;
}
return p;
}
(4)求表长
int Length(LinkList L)
{
Node* p = L->next;
int len = 0;
while (p != NULL)
{
p = p->next;
len++;
}
return len;
}
(5)打印链表
void PrintList(LinkList L)
{
Node* p = L->next;
while (p != NULL)
{
printf("%d ", p->data);
p = p->next;
}
}
(6)建立单链表
a.尾插法建立单链表
LinkList List_TailInsert(LinkList L)//每次在表尾插入一个元素
{
L->next = NULL;
int x = 0;//要插入的元素
Node* s, * r = L;
scanf("%d", &x);
while (x != -1)//这里的-1时随便取的,你可以按自己喜好取
{ //设置一个指针始终指向表尾,这样尾插时不需要遍历整个链表
s = (Node*)malloc(sizeof(Node));//这样可以减少时间复杂度
s->data = x;
r->next = s;
r = s;
scanf("%d", &x);
}
r->next = NULL;
return L;
}
b.头插法建立单链表
LinkList List_HeadInsert(LinkList L)//每次在表头插入一个元素
{
int x = 0;
L->next = NULL;
Node* s;
scanf("%d", &x);
while (x != -1)
{
s = (Node*)malloc(sizeof(Node));
s->data = x;
s->next = L->next;
L->next = s;
scanf("%d", &x);
}
return L;
}
注意到头插法建立的单链表的元素与输入的元素顺序相反,这点可以用于链表逆置,下面给出代码:
LinkList List_Reverse(LinkList L)
{
Node* p = (Node*)malloc(sizeof(Node));//将p指针所指结点头插方式插入表头
Node* q = (Node*)malloc(sizeof(Node));//q指针始终指向p所指结点的下一个结点
p = L->next;
L->next = NULL;
while (p)//根据头插法思想,不断将链表逆置
{
q = p->next;
p->next = L->next;
L->next = p;
p = q;
}
return L;
}