深度学习-线性回归

线性回归

回归分析

回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。例如，司机的鲁莽驾驶与道路交通事故数量之间的关系等等，最好的研究方法就是回归。

连续值预测

x:input
f(x):prediction
y:real data,ground-truth
给定输入数据x,在经过模型结构f以及模型的参数θ后,给出一个响应fθ(x)，若fθ(x)~>y,就能接近0误差预测到未来的数据。

根据时间的变化预测股市的波动情况

这个模型给出了股市前一两年的股市变动情况,我们想根据过去一段时间的情况预测未来股市的一个变动情况。蓝色的线代表过去一两年的股市变动情况x,黄色的线代表模型的输出fθ(x),绿色的线代表接下来一段时间股市真实的情况y,如果黄色的线能够比较逼近于绿色的线,即fθ(x)~>y,就能接近0误差预测到股市的变动情况。

线性回归

线性回归是回归问题中的一种，线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程。正常情况下的线性方程是:y=wx+b,但是我们观测到的数据往往是带有噪声的,于是我们给现有的模型一个因子,并假设该因子符合标准正态分布。此外,我们通过大量的数据来减少数据的误差,就能精准的求出w和b.

于是我们通过大量数据求解出了线性模型中w和b两个参数,并给定一个因子,该因子符合标准正态分布.给定任何一个x,就能得到y,通过这种方式,我们得到了100个样本对(x,y),绘制成图像如下:

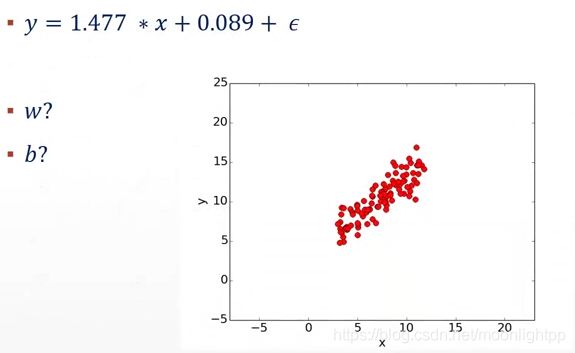
但是现实生活中我们无法得知这100个样本对(x,y)究竟符合哪种分布,它可以是线性分布,也可能是二次分布或者指数分布,那么我们该如何确定这个目标函数.

损失函数

为了得到目标函数,我们构造出了loss函数。对于任何一个x,当它经过w’x+b’-y运算后,极有可能满足w’x+b’~>y，即w’x+b’非常接近于y。也就是说,损失函数越小,就代表模型拟合的越好,越接近目标函数。那么这种情况下的w和b,就是我们要求解的线性模型的参数。

梯度下降

为了求loss函数的极小值,梯度的方向应该是函数值增大的方向,也就是梯度的反方向。此外,目标函数中有两个参数w,b,这两个参数的梯度都在发生变化。

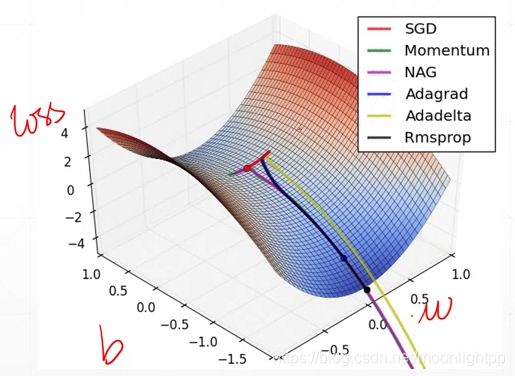
由于梯度变化幅度是一个对w的偏导,又或者是一个对b的偏导,步长太大,所以我们在偏导前面加一个衰减因子或者学习率,给定的取值范围是[0,1]。

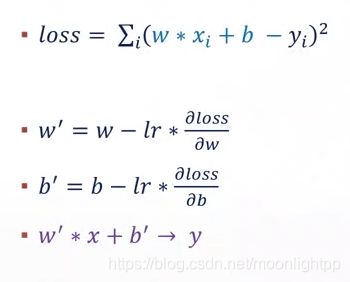
求解步骤

步骤一 计算均方误差

由于有100个样本对,每个样本对都有x,y两个数值,我们用[100,2]的数组对它们进行存放。

def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # 计算误差和
        totalError += (y - (w * x + b)) ** 2
    return totalError / float(len(points))

步骤二 计算梯度和更新w,b

def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # 计算数据集的梯度和
        w_gradient += (2 / N) * x * ((w_current * x + b_current) - y)
        b_gradient += (2 / N) * ((w_current * x + b_current) - y)
    # 更新w、b
    new_w = w_current - (learningRate * w_gradient)
    new_b = b_current - (learningRate * b_gradient)
    return [new_b, new_w]

步骤三 梯度下降迭代

def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    # update for several times
    for i in range(num_iterations):
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]

迭代1000次后的运行结果