身份证上男女识别--非线性问题02

背景

我们在上一篇中采用单层网络的模型进行了身份证男女识别，在经过多次训练发现平均误差在0.46左右，误差比较大，说明单层网络模型无法解决这个问题。我们也提出了神经网络的优化方法-，主要是全连接神经网络。

多层全连接神经网络

矩阵乘法

  设矩阵A,B，其中矩阵A是2X3，矩阵B是3X4，将矩阵A和矩阵B叉乘，即将A矩阵的每一行和B矩阵的每一列相乘，得到矩阵C（2X4）。我们在Python进行验证：

import numpy as np
a =[[1,2,3],[4,5,6]]
b =[[1,2,3,4],[5,6,7,8],[9,0,1,2]]
c=np.matmul(a,b)
print(c)

  运行结果：

[[38 14 20 26]
 [83 38 53 68]]

矩阵乘法在全连接层应用

  我们采用前面的三好学生问题来使用矩阵乘法实现全连接关系，如图1.1所示。
        矩阵乘法表示全连接层展示图

使用均方误差作为计算误差的方法

  我们之前就是误差loss的时候，使用的都是：

loss=tf.abs(y-yTrain)

  这种形式来计算误差更加适合数值范围较大的情况，例如天气的温度、证劵的价格以及三好学生的总成绩问题。
  均方误差是神经网络中国的一种误差计算方法，是指结果值向量中各数据项偏离目标值的距离平方和的平均数，也就是误差平方和的平均数。如果对于三好学生评选结果问题使用均方误差的方法，需要先把每个计算结果转换成一个二维向量，例如原来结果是1，需要变成[1,0]；
  如果原来结果是0，需要变成[0,1]；如果结果是0,2，则需要变成[0.2,0.8]，其中第一个数字代表“是三好学生的概率”，第二个数字代表“不是三好学生的概率”，那么如果计算结果是[0.2,0.8]，目标值是[1,0]，那么均方误差是：  对于二分类问题，均方误差其实一般会把误差缩小，但是误差在[0,1]范围之内。我们通过下面代码进行验证：

# Author:北京
# QQ:838262020
# time:2021/4/21
import tensorflow as tf

y = tf.placeholder(dtype=tf.float32)
yTrain = tf.placeholder(dtype=tf.float32)

loss = tf.reduce_mean(tf.square(y - yTrain))

sess = tf.Session()

print(sess.run(loss, feed_dict={
     y: [0.2, 0.8], yTrain: [1, 0]}))
print(sess.run(loss, feed_dict={
     y: [0.2, 0.8], yTrain: [0, 1]}))
print(sess.run(loss, feed_dict={
     y: [1.0, 0.0], yTrain: [0, 1]}))
print(sess.run(loss, feed_dict={
     y: [1.0, 0.0], yTrain: [1, 0]}))

  其中tf.squre函数是求平方值的函数，tf.reduce_mean函数可以对一个矩阵（或向量）中的所有数求得一个平方数。
  运行结果：

0.64
0.04
1.0
0.0

激活函数tanh

  我们前面使用够sigmoid函数的作用把任意一个数字收敛到[0,1]的范围之内，从而把一组线性数据转化为非线性数据。而tanh函数和sigmoid函数类似，将线性数据转化为非线性数据，与sigmoid函数的区别在于tanh函数将任意一个数字转换为[-1,1]之间。

新的模型

身份证问题的模型改成多层全连接神经网络模型，如图所示
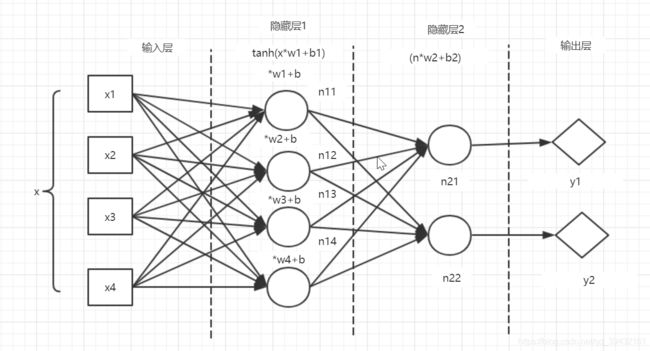具体代码实现：

# Author:北京
# QQ:838262020
# time:2021/4/21
import tensorflow as tf
import random
random.seed()

x=tf.placeholder(tf.float32)
yTrain=tf.placeholder(tf.float32)

w1=tf.Variable(tf.random_normal([4,8],mean=0.5,stddev=0.1),dtype=tf.float32)
b1=tf.Variable(0,dtype=tf.float32)
xr=tf.reshape(x,[1,4])
n1=tf.nn.tanh(tf.matmul(xr,w1)+b1)

w2=tf.Variable(tf.random_normal([8,2],mean=0.5,stddev=0.1),dtype=tf.float32)
b2=tf.Variable(0,dtype=tf.float32)

n2=tf.matmul(n1,w2)+b2

y=tf.nn.softmax(tf.reshape(n2,[2]))

loss =tf.reduce_mean(tf.square(y-yTrain))

optimizer=tf.train.RMSPropOptimizer(0.01)
train=optimizer.minimize(loss)
sess=tf.Session()
sess.run(tf.global_variables_initializer())

lossSum=0.0
for i in range(50000):
    # 随机产生[0,9]的4位整数，模拟身份证后4位
    xDataRandom = [int(random.random() * 10), int(random.random() * 10), int(random.random() * 10),
                   int(random.random() * 10)]
    # 判断倒数第2位数字奇数或者偶数来模型对应的性别男女
    if xDataRandom[2] % 2 == 0:
        yTrainDataRandom = [0,1]
    else:
        yTrainDataRandom = [1,0]

    result = sess.run([train, x, yTrain, y, loss], feed_dict={
     x: xDataRandom, yTrain: yTrainDataRandom})
    lossSum = lossSum + float(result[len(result) - 1])
    print("i:%d,loss:%10.10f,avgLoss:%10.10f" % (i, float(result[len(result) - 1]), lossSum / (i + 1)))

运行结果：

i:49991,loss:0.0007885849,avgLoss:0.2097267489
i:49992,loss:0.6985108852,avgLoss:0.2097365259
i:49993,loss:0.0428997725,avgLoss:0.2097331888
i:49994,loss:0.0306137353,avgLoss:0.2097296061
i:49995,loss:0.0014930198,avgLoss:0.2097254410
i:49996,loss:0.0274514221,avgLoss:0.2097217953
i:49997,loss:0.0245045219,avgLoss:0.2097180908
i:49998,loss:0.6867797375,avgLoss:0.2097276322
i:49999,loss:0.0480841063,avgLoss:0.2097243994