数值分析(一) 牛顿插值法及matlab代码
目录
- 数学: 数值分析
- 一、牛顿插值法原理
-
- 1.牛顿插值多项式
- 2.差商
-
- 2.1 定义
- 2.2 性质
- 2.3 差商表
- 3.牛顿(Newton)插值公式
- 二、牛顿插值公式matlab代码
-
- 1. matlab实时在线脚本
- 2. 牛顿插值代码
- 3.实例
- 三、总结
- 四、补充
数学: 数值分析
刚上完数值分析课在其中学习了不少的知识,课后还做了一些课程实验主要都是利用matlab编程来解决问题,接下先讲插值法中的牛顿插值法
一、牛顿插值法原理
1.牛顿插值多项式
定义牛顿插值多项式为:
N n ( x ) = a 0 + a 1 ( x − x 0 ) + a 2 ( x − x 0 ) ( x − x 1 ) + ⋯ + a n ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n − 1 ) N_n\left(x\right)=a_0+a_1\left(x-x_0\right)+a_2\left(x-x_0\right)\left(x-x_1\right)+\cdots+a_n\left(x-x_0\right)\left(x-x_1\right)\cdots\left(x-x_{n-1}\right) Nn(x)=a0+a1(x−x0)+a2(x−x0)(x−x1)+⋯+an(x−x0)(x−x1)⋯(x−xn−1) 其中 a k ( k = 0 , 1 , 2 , ⋯ , n ) a_k\left(k=0,1,2,\cdots,n\right) ak(k=0,1,2,⋯,n)为待定系数
可见,牛顿插值多项式 N ( x ) N\left(x\right) N(x)是插值多项式 P ( x ) P\left(x\right) P(x)的另一种表示形式, 与Lagrange多项式相比它不仅克服了“增加一个节点时整个计算工作重新开始”的缺点, 且可以节省乘除法运算次数, 同时在Newton插值多项式中用到差分与差商等概念,又与数值计算的其他方面有密切的关系.
2.差商
2.1 定义
自变量之差与因变量之差之比叫差商
定义: 函数 y = f ( x ) y=f\left(x\right) y=f(x)在区间 [ x i , x i + 1 ] \left[x_i,x_{i+1}\right] [xi,xi+1]上的平均变化率 f [ x i , x i + 1 ] = f ( x i + 1 ) − f ( x i ) x i + 1 − x i f\left[x_i,x_{i+1}\right]=\frac{f\left(x_{i+1}\right)-f\left(x_i\right)}{x_{i+1}-x_i} f[xi,xi+1]=xi+1−xif(xi+1)−f(xi) 称为 f ( x ) f\left(x\right) f(x)关于 x i , x i + 1 x_i,x_{i+1} xi,xi+1的一阶差商,并记为 f [ x i , x i + 1 ] f\left[x_i,x_{i+1}\right] f[xi,xi+1]
二阶差商: f [ x i , x i + 1 , x i + 2 ] = f [ x i + 1 , x i + 2 ] − f [ x i , x i + 1 ] x i + 2 − x i f\left[x_i,x_{i+1},x_{i+2}\right]=\frac{f\left[x_{i+1},x_{i+2}\right]-f\left[x_i,x_{i+1}\right]}{x_{i+2}-x_i} f[xi,xi+1,xi+2]=xi+2−xif[xi+1,xi+2]−f[xi,xi+1] m阶差商: f [ x 0 , x 1 , ⋯ , x m ] = f [ x 1 , x 2 , ⋯ , x m ] − f [ x 0 , x 1 , ⋯ , x m − 1 ] x m − x 0 f\left[x_0,x_1,\cdots,x_m\right]=\frac{f\left[x_1,x_2,\cdots,x_m\right]-f\left[x_0,x_1,\cdots,x_{m-1}\right]}{x_m-x_0} f[x0,x1,⋯,xm]=xm−x0f[x1,x2,⋯,xm]−f[x0,x1,⋯,xm−1]
2.2 性质
性质1:函数 f ( x ) f\left(x\right) f(x)的 n 阶差商 f [ x 0 , x 1 , ⋯ , x n ] f\left[x_0,x_1,\cdots,x_n\right] f[x0,x1,⋯,xn]可由函数值 f ( x 0 ) , f ( x 1 ) , ⋯ , f ( x n ) f\left(x_0\right),f\left(x_1\right),\cdots,f\left(x_n\right) f(x0),f(x1),⋯,f(xn) 的线性组合表示, 且 f [ x 0 , x 1 , ⋯ , x n ] = ∑ k = 0 n f ( x k ) ω ′ ( x k ) = ∑ k = 0 n f ( x k ) ( x k − x 0 ) ( x k − x 1 ) ⋯ ( x k − x k − 1 ) ( x − x k + 1 ) ⋯ ( x k − x n ) f\left[x_0,x_1,\cdots,x_n\right]=\sum_{k=0}^n\frac{f\left(x_k\right)}{\omega'\left(x_k\right)}\\=\sum_{k=0}^n\frac{f\left(x_k\right)}{\left(x_k-x_0\right)\left(x_k-x_1\right)\cdots\left(x_k-x_{k-1}\right)\left(x-x_{k+1}\right)\cdots\left(x_k-x_n\right)} f[x0,x1,⋯,xn]=k=0∑nω′(xk)f(xk)=k=0∑n(xk−x0)(xk−x1)⋯(xk−xk−1)(x−xk+1)⋯(xk−xn)f(xk)其中 ω ′ ( x k ) = ∏ i = 0 , i ≠ k n ( x k − x i ) \omega'\left(x_k\right)=\prod_{i=0,i\neq k}^n\left(x_k-x_i\right) ω′(xk)=i=0,i=k∏n(xk−xi)
性质2:差商具有对称性,即在k阶差商中 f [ x 0 , x 1 , ⋯ , x n ] f\left[x_0,x_1,\cdots,x_n\right] f[x0,x1,⋯,xn]任意交换两个节点 x i x_i xi和 x j x_j xj的次序,其值不变。
例如: f [ x 0 , x 1 , x 2 ] = f [ x 1 , x 2 , x 0 ] = f [ x 0 , x 2 , x 1 ] = ⋯ f\left[x_0,x_1,x_2\right]=f\left[x_1,x_2,x_0\right]=f\left[x_0,x_2,x_1\right]=\cdots f[x0,x1,x2]=f[x1,x2,x0]=f[x0,x2,x1]=⋯ 性质3:k阶差商 f [ x 0 , x 1 , ⋯ , x k ] f\left[x_0,x_1,\cdots,x_k\right] f[x0,x1,⋯,xk]和k阶导数之间有下列关系 f [ x 0 , x 1 , ⋯ , x k ] = f ( k ) ( ξ ) k ! ξ ∈ ( m i n 0 ≤ i ≤ n x i , m a x 0 ≤ i ≤ n x i ) f\left[x_0,x_1,\cdots,x_k\right]=\frac{f^{\left(k\right)}\left(\xi\right)}{k!}\;\;\;\;\;\;\;\xi\in\left(\underset{0\leq i\leq n}{min}x_i,\underset{0\leq i\leq n}{max}x_i\right) f[x0,x1,⋯,xk]=k!f(k)(ξ)ξ∈(0≤i≤nminxi,0≤i≤nmaxxi)
2.3 差商表
| x i x_i xi | f [ x i ] f\left[x_i\right] f[xi] | f [ x i , x i + 1 ] f\left[x_i,x_{i+1}\right] f[xi,xi+1] | f [ x i , x i + 1 , x i + 2 ] f\left[x_i,x_{i+1},x_{i+2}\right] f[xi,xi+1,xi+2] | f [ x i , x i + 1 , x i + 2 , x i + 3 ] f\left[x_i,x_{i+1},x_{i+2},x_{i+3}\right] f[xi,xi+1,xi+2,xi+3] | ⋯ \cdots ⋯ |
|---|---|---|---|---|---|
| x 0 x_0 x0 | f ( x 0 ) f\left(x_0\right) f(x0) | ||||
| x 1 x_1 x1 | f ( x 1 ) f\left(x_1\right) f(x1) | f [ x 0 , x 1 ] f\left[x_0,x_1\right] f[x0,x1] | |||
| x 2 x_2 x2 | f ( x 2 ) f\left(x_2\right) f(x2) | f [ x 1 , x 2 ] f\left[x_1,x_2\right] f[x1,x2] | f [ x 0 , x 1 , x 2 ] f\left[x_0,x_1,x_2\right] f[x0,x1,x2] | ||
| x 3 x_3 x3 | f ( x 3 ) f\left(x_3\right) f(x3) | f [ x 2 , x 3 ] f\left[x_2,x_3\right] f[x2,x3] | f [ x 1 , x 2 , x 3 ] f\left[x_1,x_2,x_3\right] f[x1,x2,x3] | f [ x 0 , x 1 , x 2 , x 3 ] f\left[x_0,x_1,x_2,x_3\right] f[x0,x1,x2,x3] | |
| ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ | ⋯ \cdots ⋯ |
3.牛顿(Newton)插值公式
由之前牛顿插值多项式和差商可推出牛顿插值公式其中系数 a 0 = f ( x 0 ) a_0=f\left(x_0\right) a0=f(x0) a 1 = f [ x 0 , x 1 ] a_1=f\left[x_0,x_1\right] a1=f[x0,x1] a 2 = f [ x 0 , x 1 , x 2 ] a_2=f\left[x_0,x_1,x_2\right] a2=f[x0,x1,x2] 其中一般式: a k = f [ x 0 , x 1 , ⋯ , x k ] ( k = 0 , 1 , ⋯ , n ) a_k=f\left[x_0,x_1,\cdots,x_k\right]\;\;\;\;\;\left(k=0,1,\cdots,n\right) ak=f[x0,x1,⋯,xk](k=0,1,⋯,n) 将求得系数代入多项式中即可得到n次牛顿插值公式 N n ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + ⋯ + f [ x 0 , x 1 , ⋯ , x n ] ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n ) N_n\left(x\right)=f\left(x_0\right)+f\left[x_0,x_1\right]\left(x-x_0\right)+\cdots+f\left[x_0,x_1,\cdots,x_n\right]\left(x-x_0\right)\left(x-x_1\right)\cdots\left(x-x_n\right) Nn(x)=f(x0)+f[x0,x1](x−x0)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn) 其余项为 R n ( x ) = f [ x 0 , x 1 , ⋯ , x n , x ] ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n ) = f [ x 0 , x 1 , ⋯ , x n , x ] ∏ i = 0 n ( x − x i ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ∏ i = 0 n ( x − x i ) f [ x 0 , x 1 , ⋯ , x n ] = f ( n + 1 ) ( ξ ) ( n + 1 ) ! R_n\left(x\right)=f\left[x_0,x_1,\cdots,x_n,x\right]\left(x-x_0\right)\left(x-x_1\right)\cdots\left(x-x_n\right)\\=f\left[x_0,x_1,\cdots,x_n,x\right]\prod_{i=0}^n\left(x-x_i\right)=\frac{f^{\left(n+1\right)}\left(\xi\right)}{\left(n+1\right)!}\prod_{i=0}^n\left(x-x_i\right)\\f\left[x_0,x_1,\cdots,x_n\right]=\frac{f^{\left(n+1\right)}\left(\xi\right)}{\left(n+1\right)!} Rn(x)=f[x0,x1,⋯,xn,x](x−x0)(x−x1)⋯(x−xn)=f[x0,x1,⋯,xn,x]i=0∏n(x−xi)=(n+1)!f(n+1)(ξ)i=0∏n(x−xi)f[x0,x1,⋯,xn]=(n+1)!f(n+1)(ξ)
二、牛顿插值公式matlab代码
友情提示:本人使用的是matlab2019b版本,并且个人很喜欢使用matlab中的实时在线脚本,很少使用脚本来编写程序。实时在线脚本脚本编译环境我个人非常喜欢,所以接下来的代码都是在实时在线脚本中实现,简要的讲一下实时在线脚本
1. matlab实时在线脚本
简要介绍一下实时在线脚本,首先打开matlab,可以看到一下界面,点击实时在线脚本
基本打开后就可以看到这样一个界面如下图所示,还有很多功能等待读者自己去体会简要概述讲到这里
给大家看一下编写代码后的部分样子,函数,代码,结果分块显示非常清晰,与脚本的区别还是很大的,大家特别注意一下脚本生成的文件为.m文件,实时在线脚本脚本为.mlx文件
2. 牛顿插值代码
下面展示牛顿插值函数代码
function [A,y]= newtonzi(X,Y,x)
% Newton插值函数
% X为已知数据点的x坐标
% Y为已知数据点的y坐标
% x为插值点的x坐标
% 函数返回A差商表
% y为各插值点函数值
n=length(X); m=length(x);
for t=1:m
z=x(t); A=zeros(n,n);A(:,1)=Y';
s=0.0; y=0.0; c1=1.0;
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));
end
end
C=A(n,n);
for k=1:n
p=1.0;
for j=1:k-1
p=p*(z-X(j));
end
s=s+A(k,k)*p;
end
ss(t)=s;
end
y=ss;
A=[X',A];
end
3.实例
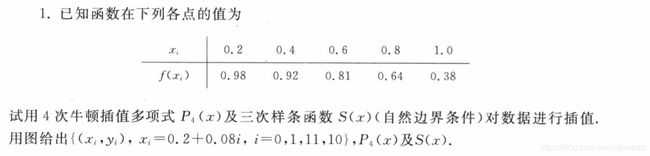
选取的实例是以教材《数值分析》(第五版 李庆扬)第二章 插值法计算实习题题目如下:
这里先解决牛顿插值多项式,利用之前编写的牛顿插值函数
下面展示代码
x=0.2:0.2:1;
y=[0.98 0.92 0.81 0.64 0.38];
x0=[0.2 0.28 1.0 1.08];
[d,y]=newtonzi(x,y,x0) %调用牛顿插值函数
运行后的结果如下 d为差商表,y为插值点 x 0 x_0 x0对应的纵坐标

在实时在线脚本中代码结果全样貌如下图所示

根据计算结果得到牛顿4次插值公式为:
P 4 ( x ) = 0.98 − 0.3 ( x − 0.2 ) − 0.625 ( x − 0.2 ) ( x − 0.4 ) − 0.2083 ( x − 0.2 ) ( x − 0.4 ) ( x − 0.6 ) − 0.5208 ( x − 0.2 ) ( x − 0.4 ) ( x − 0.6 ) ( x − 0.8 ) P_4\left(x\right)=0.98-0.3\left(x-0.2\right)-0.625\left(x-0.2\right)\left(x-0.4\right)-0.2083\left(x-0.2\right)\left(x-0.4\right)\left(x-0.6\right)\\-0.5208\left(x-0.2\right)\left(x-0.4\right)\left(x-0.6\right)\left(x-0.8\right) P4(x)=0.98−0.3(x−0.2)−0.625(x−0.2)(x−0.4)−0.2083(x−0.2)(x−0.4)(x−0.6)−0.5208(x−0.2)(x−0.4)(x−0.6)(x−0.8)
三、总结
此次内容主要讲的是牛顿插值的原理,及根据原理利用matlab编写一个通用计算公式函数,然后举例来验证代码的正确性。此次例题中提到了一个三次样条插值函数,将会放在下篇更新。本人第一次写csdn,也是第一次发表,有些地方存在问题希望读者多多指正,也感谢大家多多关注本人。
顺便问下有没有cug的校友,多支持一下。谢谢读者耐心的观看本篇文章。
四、补充
下一篇文章1 : 数值分析(二) 三次样条插值法matlab代码
下一篇文章 2: 数值分析(二续) 三次样条插值二类边界完整matlab代码