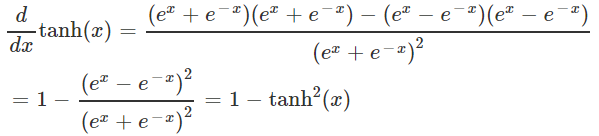PyTorch系列学习笔记07 - 随机梯度下降
PyTorch系列学习笔记07 - 随机梯度下降
- 07 随机梯度下降
-
- 7.1 什么是梯度?
-
- 梯度在深度学习中是如何发挥作用的?
- 梯度下降算法面临的两个问题:局部极小值与鞍点
- 除了损失函数本身以外影响优化器性能的因素
- 7.2 常见函数的梯度
-
- 感知机函数
- PyTorch自动求导机制
-
- torch.autograd.grad()
- loss.backward()
- 7.3 激活函数的梯度
-
- 最初的激活函数
- Sigmoid / Logistic
- Tanh
- ReLU
-
- PyTorch API
- Softmax
- 7.4 Loss的梯度
-
- Mean Squared Error,MSE
- Cross Entropy,CE
- 7.5 单层感知机(Perception)的梯度计算与参数更新
-
- 单层单输出感知机梯度计算及参数更新过程
- 单层多输出感知机梯度计算及参数更新过程
- 7.6 链式法则
- 7.7 多层感知机(MLP)反向传播算法
- 7.8 2D函数(Himmelblau function)优化问题实战
- Reference
07 随机梯度下降
在前几章中,介绍了使用PyTorch对Tensor进行基本的操作,如维度变换、计算等。这些操作都是为了本节的内容做铺垫,梯度是深度学习中最为核心的概念,梯度下降算法是神经网络能够学习知识的最为关键的工具。本节将对梯度下降算法进行介绍。
7.1 什么是梯度?
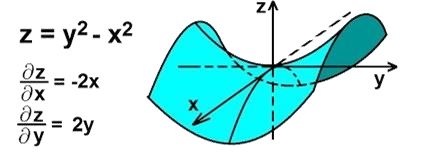
梯度是从导数衍生出来的一个概念,表示某一函数在该点处的方向导数沿着该方向取得最大值。
- 导数(derivate)
- 偏导数(partial derivate)
- 梯度(gradient)是一个向量,对于 f ( x 1 , x 2 , . . . , x n ) f(x_1, x_2, ...,x_n) f(x1,x2,...,xn),其梯度表达式为: ∇ f = ( ∂ f ∂ x 1 , ∂ f ∂ x 2 , . . . , ∂ f ∂ x n ) \nabla f=(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},...,\frac{\partial f}{\partial x_n}) ∇f=(∂x1∂f,∂x2∂f,...,∂xn∂f)
导数反映了函数在某一点处的变化趋势,梯度既有大小,又有方向,是一个矢量。梯度的方向代表了函数值增长最快的方向,梯度的大小表示了沿着该方向的方向导数的值,即函数值增长的速率。
 |
|---|
梯度在深度学习中是如何发挥作用的?
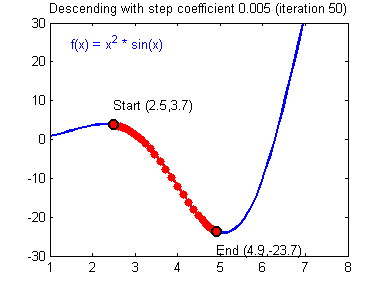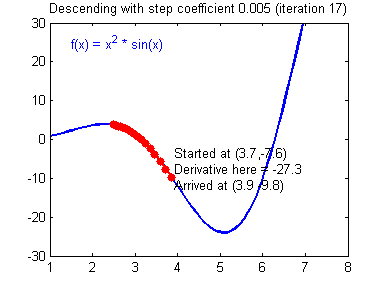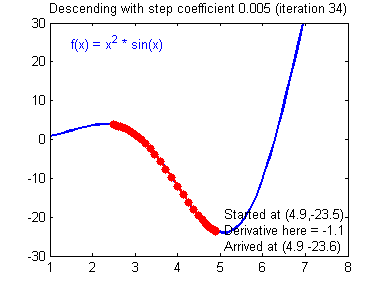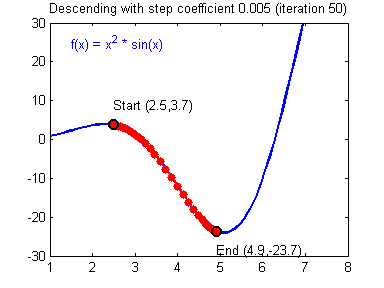
深度学习所要解决的问题可以理解为一个最优化问题,即寻找到一个最大值或者最小值的问题。梯度既然代表了函数在某一点处增长最快的方向,那么顺着该方向,就能够找到一个函数的极大值或者极小值。
深度学习一般设置最小化损失函数 loss 为目标函数,所以梯度在深度学习中的应用就是 如何找到一个极小值 的问题。
神经网络中的参数更新公式: θ t + 1 = θ t − α t ∗ ∇ f ( θ t ) \theta_{t+1}=\theta_t-\alpha_t*\nabla f(\theta_t) θt+1=θt−αt∗∇f(θt)其中, α t \alpha_t αt 一般为学习率,一般设置为较小的值,如 0.001, ∇ f ( θ t ) \nabla f(\theta_t) ∇f(θt) 表示梯度,负号表示沿梯度反方向,即函数值减小的方向。
举个栗子:
对于包含两个参数 θ 1 , θ 2 \theta_1, \theta_2 θ1,θ2 的函数 J ( θ 1 , θ 2 ) J(\theta_1, \theta_2) J(θ1,θ2),其参数更新的过程如下所示:

如果参数初始化恰好取到了 ( θ 1 , θ 2 ) = ( 0 , 0 ) (\theta_1, \theta_2)=(0, 0) (θ1,θ2)=(0,0) ,那么参数更新后还是 ( θ 1 , θ 2 ) = ( 0 , 0 ) (\theta_1, \theta_2)=(0, 0) (θ1,θ2)=(0,0),说明此时恰好取到了一个极小值,根据对该函数的了解我们知道该点恰好是它的最小值。
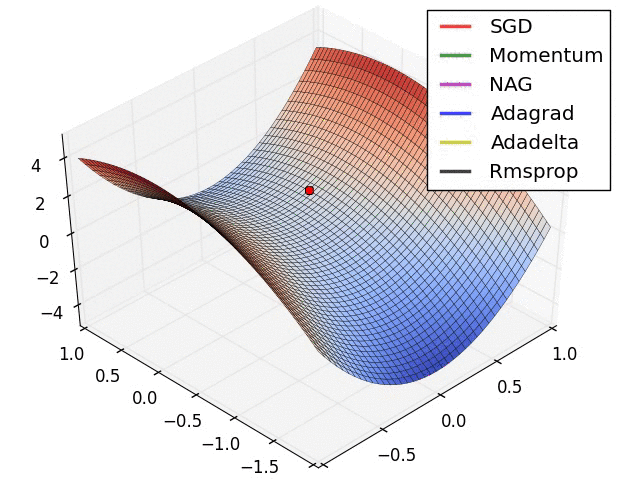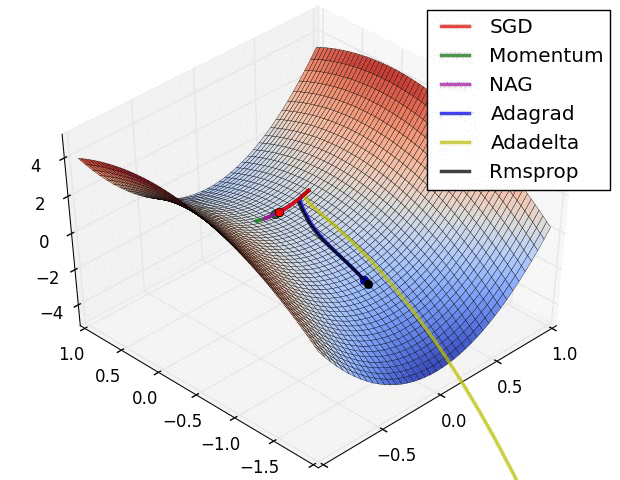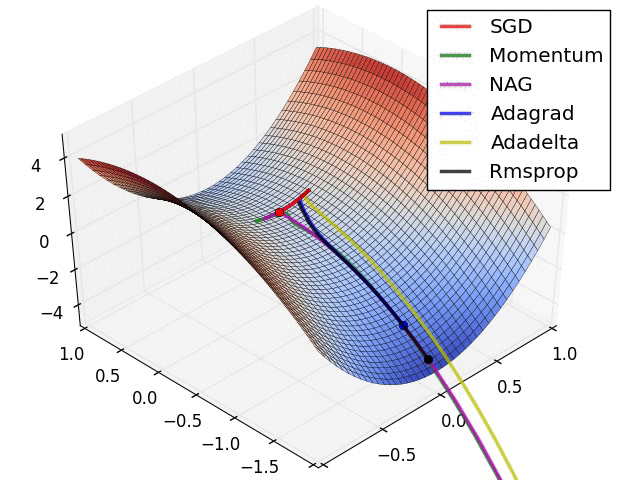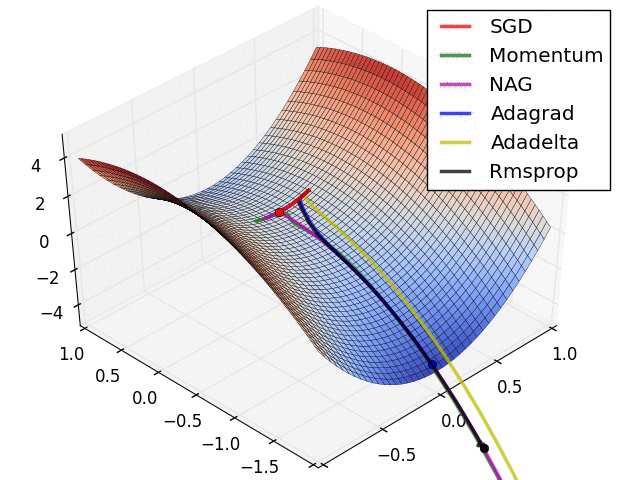
下图展示了梯度更新的过程:
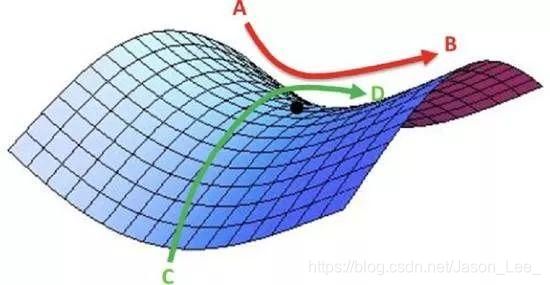
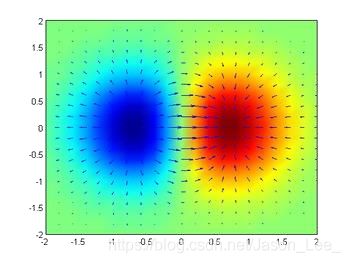
梯度下降算法面临的两个问题:局部极小值与鞍点
局部极小值
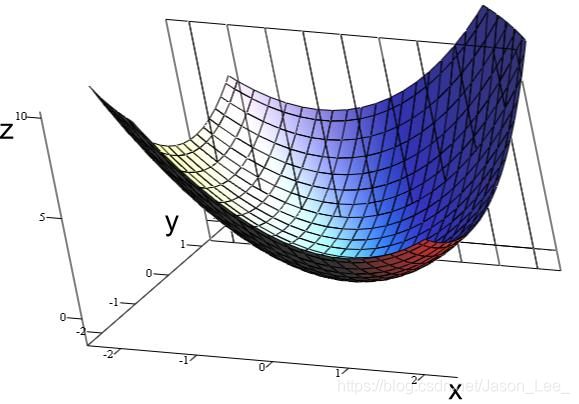
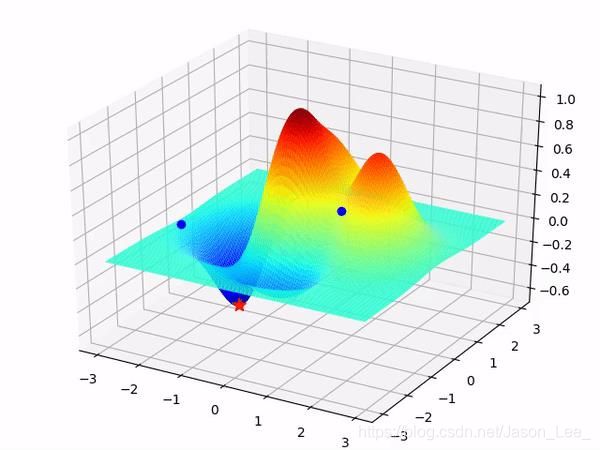
对于目标函数是凸函数(Convex function)的优化问题,其极值点必然是最值点,所以必然能够找到最优值。这也是比较简单的一种情况,但是对于梯度下降算法也面临着一个问题:利用梯度下降算法得到的结果可能只是极小值,而非最小值。
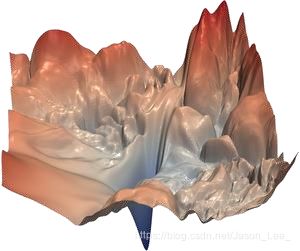
对于这些情况,很难找到最小值。在ResNet中,添加了 “skip” 连接后,loss函数简化成了下图所示的情况:
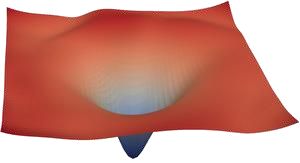
鞍点
下图中所示的点就是鞍点,在鞍点位置,梯度同样为0,其沿着 x 和 y 方向的导数均为 0 ,所以参数不再更新。在这种情况下,其在参数 w 1 w_1 w1 维度上取得极小值,但是在参数 w 2 w_2 w2 维度上却取得了一个极大值。 在深度学习中,参数数量往往是百万级别的,所以会不可避免的遇到两个参数出现鞍点情况。
除了损失函数本身以外影响优化器性能的因素
- 初始状态
- 学习率
- 动量
- 等等…
初始状态的选取对优化器性能的影响
选取不同的初始值可能会取得极小值也可能取得最小值。
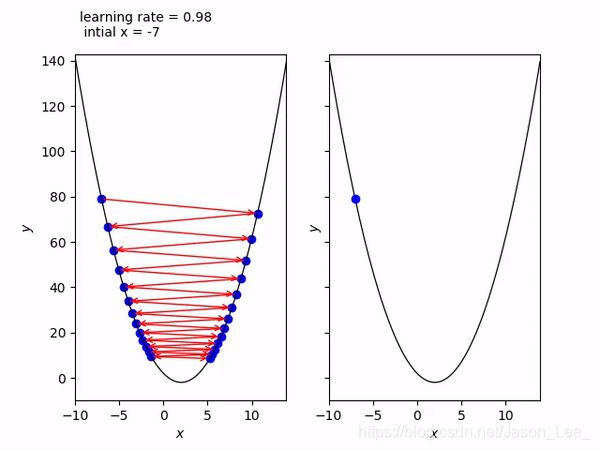
学习率的设置对优化器性能的影响
学习率设置过大,可能会导致震荡。
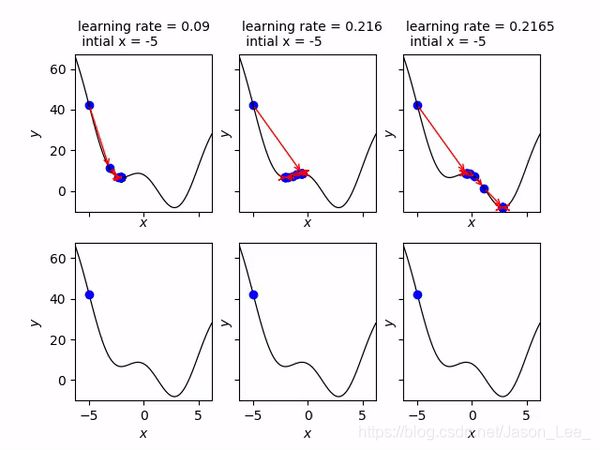
添加动量对优化器性能的影响
在优化器中加入动量,可能会使得参数根据之前移动的惯性跳出极小值。
7.2 常见函数的梯度
感知机函数
不使用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是 最原始的感知机(Perceptron) 。
感知机线性模型可以表示为: f ( x ) = w ∗ x + b ∂ f ∂ w = x ∂ f ∂ b = 1 ∇ ( w , b ) = ( x , 1 ) \begin{aligned} & f(x)=w*x+b \\ \\ & \frac{\partial{f}}{\partial{w}}=x \\ & \frac{\partial{f}}{\partial{b}}=1 \\ & \nabla_{(w,b)}=(x, 1) \end{aligned} f(x)=w∗x+b∂w∂f=x∂b∂f=1∇(w,b)=(x,1)
PyTorch自动求导机制
在PyTorch中,用来实现自动求导机制的API主要有两个:
torch.autograd.grad(loss, [w1, w2, ...])
使用该API可以指定对哪些参数求导,并直接返回求导得到的张量(对几个参数计算梯度,就返回几个参数的张量)。loss.backward()与w.grad
使用该API会直接对所有设置了requires_grad的参数求导,且该方法无返回值,会直接将计算得到的梯度附加在原张量之上,可以使用w.grad查看参数w的梯度信息。
torch.autograd.grad()
PyTorch自动求导API:torch.autograd.grad()
torch.autograd.grad(outputs, inputs, grad_outputs=None, retain_graph=None, create_graph=False, only_inputs=True, allow_unused=False)
"""
outputs: 输出函数 y
inputs: 需要进行求导的参数 θ=[w1, w2, ...]
即outputs对inputs进行求导:dy/dθ
retain_graph: 如果设置为False,则计算完梯度后,用来计算梯度的计算图会被释放,再次执行梯度计算操作,会报错:
RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.
create_graph: 如果设置为“True”,则为导数创建计算图,并设置requires_grad=True,
可以对其求高阶导数,默认为“False”,不可求高阶导数。
"""
# =================源码==========================
def grad(outputs, inputs, grad_outputs=None, retain_graph=None, create_graph=False,
only_inputs=True, allow_unused=False):
"""Computes and returns the sum of gradients of outputs w.r.t. the inputs.
``grad_outputs`` should be a sequence of length matching ``output``
containing the pre-computed gradients w.r.t. each of the outputs. If an
output doesn't require_grad, then the gradient can be ``None``).
If ``only_inputs`` is ``True``, the function will only return a list of gradients
w.r.t the specified inputs. If it's ``False``, then gradient w.r.t. all remaining
leaves will still be computed, and will be accumulated into their ``.grad``
attribute.
Arguments:
outputs (sequence of Tensor): outputs of the differentiated function.
inputs (sequence of Tensor): Inputs w.r.t. which the gradient will be
returned (and not accumulated into ``.grad``).
grad_outputs (sequence of Tensor): Gradients w.r.t. each output.
None values can be specified for scalar Tensors or ones that don't require
grad. If a None value would be acceptable for all grad_tensors, then this
argument is optional. Default: None.
retain_graph (bool, optional): If ``False``, the graph used to compute the grad
will be freed. Note that in nearly all cases setting this option to ``True``
is not needed and often can be worked around in a much more efficient
way. Defaults to the value of ``create_graph``.
create_graph (bool, optional): If ``True``, graph of the derivative will
be constructed, allowing to compute higher order derivative products.
Default: ``False``.
allow_unused (bool, optional): If ``False``, specifying inputs that were not
used when computing outputs (and therefore their grad is always zero)
is an error. Defaults to ``False``.
"""
if not only_inputs:
warnings.warn("only_inputs argument is deprecated and is ignored now "
"(defaults to True). To accumulate gradient for other "
"parts of the graph, please use torch.autograd.backward.")
outputs = (outputs,) if isinstance(outputs, torch.Tensor) else tuple(outputs)
inputs = (inputs,) if isinstance(inputs, torch.Tensor) else tuple(inputs)
if grad_outputs is None:
grad_outputs = [None] * len(outputs)
elif isinstance(grad_outputs, torch.Tensor):
grad_outputs = [grad_outputs]
else:
grad_outputs = list(grad_outputs)
grad_outputs = _make_grads(outputs, grad_outputs)
if retain_graph is None:
retain_graph = create_graph
return Variable._execution_engine.run_backward(
outputs, grad_outputs, retain_graph, create_graph,
inputs, allow_unused)
以 y p r e d = w ∗ x + b y_{pred}=w*x+b ypred=w∗x+b 为例展示PyTorch的自动求导机制:
# 参数初始化
In [48]: x = torch.ones(1)
In [49]: w = torch.full([1], 2, dtype=torch.float32)
In [50]: y_pred = w*x # 设置b=0
In [51]: y_label = torch.ones(1)
In [52]: mse = F.mse_loss(y_pred, y_label)
In [53]: torch.autograd.grad(mse, [w])
# 报错:RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
In [54]: w.requires_grad_()
"""
在PyTorch中所有需要计算导数的参数都需要明确制定 requires_grad 参数,
所以需要设置w为需要求导,也可以在张量定义时即声明其需要求导:
w = torch.full([1], 2, dtype=torch.float32, requires_grad=True)
"""
Out[54]: tensor([2.], requires_grad=True)
In [55]: torch.autograd.grad(mse, [w])
"""
仍然报错:RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
因为PyTorch是动态图机制(每执行一步运算,就更新一步计算图),在此处仅更新了w,
但是计算图还没有更新,使用的仍然是原来的计算图,所以w定义之后的所有的计算步骤
都需要重新执行一遍以更新计算图
"""
In [56]: y_pred = w*x # 设置b=0
In [57]: mse = F.mse_loss(y_pred, y_label)
In [58]: torch.autograd.grad(mse, [w])
Out[58]: (tensor([2.]),) # mse求导为:2*∑(wx-y_label)*x,代入对应值得到结果为 2
再举个栗子:
无论是多深的神经网络,其都可以视为一系列函数的嵌套,因此可以使用PyTorch对输出的loss对每一个weight进行自动求导。 以 y = a 2 x + b x + c y=a^2x+bx+c y=a2x+bx+c 在 x = 1 x=1 x=1 处,对 a , b , c a,b,c a,b,c 的偏导数为例: ∂ y ∂ a = 2 a x = x = 1 , a = 1 2 ∂ y ∂ b = x = x = 1 , b = 2 1 ∂ y ∂ c = 1 = x = 1 , c = 3 1 \begin{aligned} & \frac{\partial y}{\partial a}=2ax\xlongequal{x=1,a=1}2 \\ & \frac{\partial y}{\partial b}=x\xlongequal{x=1,b=2}1 \\ & \frac{\partial y}{\partial c}=1\xlongequal{x=1,c=3}1 \\ \end{aligned} ∂a∂y=2axx=1,a=12∂b∂y=xx=1,b=21∂c∂y=1x=1,c=31
import torch
from torch import autograd
x = torch.tensor(1.) # 不能对变量 x 进行求导,所以不能指定 requires_grad=True。
a = torch.tensor(1., requires_grad=True) # 参数 requires_grad=True 表示需要对其求导计算梯度
b = torch.tensor(2., requires_grad=True)
c = torch.tensor(3., requires_grad=True)
y = a**2 * x + b * x + c
print('before:', a.grad, b.grad, c.grad)
grads = autograd.grad(y, [a, b, c])
print('after :', grads[0], grads[1], grads[2])
运行结果:
# 在求导之前,没有梯度信息,输出为 None ,且只有使用loss.backward进行求导时,可以使用a.grad输出梯度信息。
before: None None None
after : tensor(2.) tensor(1.) tensor(1.)
loss.backward()
在使用 loss.backward() 进行反向传播时,会自动计算参数的梯度信息,但是,不会直接返回一个包含所有参数梯度信息的张量,而是将梯度信息附加在每个参数之后,可以使用 w.grad 查看参数 w 的梯度信息。
PyTorch API:loss.backward()
# 参数初始化
In [48]: x = torch.ones(1)
In [49]: w = torch.full([1], 2, dtype=torch.float32)
In [50]: y_pred = w*x # 设置b=0
In [51]: y_label = torch.ones(1)
In [52]: mse = F.mse_loss(y_pred, y_label)
In [53]: mse.backward()
# 使用loss.backward()同样会报错:RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
In [54]: w.requires_grad_()
"""
在PyTorch中所有需要计算导数的参数都需要明确制定 requires_grad 参数,
所以需要设置w为需要求导,也可以在张量定义时即声明其需要求导:
w = torch.full([1], 2, dtype=torch.float32, requires_grad=True)
"""
Out[54]: tensor([2.], requires_grad=True)
In [55]: mse.backward()
"""
仍然报错:RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn
因为PyTorch是动态图机制(每执行一步运算,就更新一步计算图),在此处仅更新了w,
但是计算图还没有更新,使用的仍然是原来的计算图,所以w定义之后的所有使用到参数w
的计算步骤都需要重新执行一遍以更新计算图
"""
In [56]: y_pred = w*x + 0 # 设置b=0
In [57]: mse = F.mse_loss(y_pred, y_label)
In [58]: mse.backward()
In [59]: w.grad
Out[59]: tensor([2.])
# 如果参数数量很大,梯度信息很多的话,一般采用打印范数,来查看梯度的相对大小
In [27]: w.grad.norm()
Out[27]: tensor(2.)
7.3 激活函数的梯度
激活函数(Activation functions)对于人工神经网络模型学习、理解非常复杂和非线性的函数来说具有十分重要的作用,其将非线性特性引入到神经网络中。激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
下图展示了使用了激活函数的神经元基本结构:
最初的激活函数
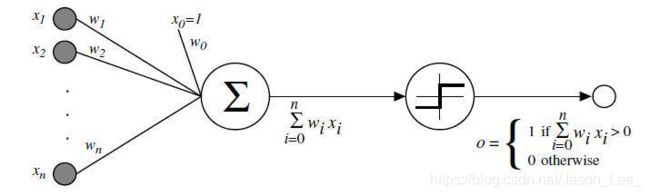
基于青蛙的神经元对于输入刺激响应阈值的原理设计出的激活函数:
 |
 |
|---|
由于该激活函数存在着不可导点,因此该函数不适用于梯度下降算法进行优化。求解这种激活函数的方法是 启发式搜索,用于求解单层感知机最优解。
Sigmoid / Logistic
Sigmoid 激活函数又称为 Logistic 激活函数,其表达式如下: f ( x ) = σ ( x ) = 1 1 + e − x ∈ ( 0 , 1 ) f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\in(0,1) f(x)=σ(x)=1+e−x1∈(0,1)可以将函数值区间压缩 ( − ∞ , + ∞ ) ⇒ ( 0 , 1 ) (-\infty,+\infty)\Rightarrow(0,1) (−∞,+∞)⇒(0,1) 。其函数曲线如下:

其导数: d d x σ ( x ) = d d x ( 1 1 + e − x ) = e − x ( 1 + e − x ) 2 = ( 1 + e − x ) − 1 ( 1 + e − x ) 2 = 1 + e − x ( 1 + e − x ) 2 − ( 1 1 + e − x ) 2 = σ ( x ) − σ ( x ) 2 ⇒ σ ′ = σ ( 1 − σ ) \begin{aligned} \frac{d}{dx}\sigma(x) & =\frac{d}{dx}(\frac{1}{1+e^{-x}}) \\ & =\frac{e^{-x}}{(1+e^{-x})^2} \\ & =\frac{(1+e^{-x})-1}{(1+e^{-x})^2} \\ & =\frac{1+e^{-x}}{(1+e^{-x})^2}-(\frac{1}{1+e^{-x}})^2 \\ & =\sigma(x)-\sigma(x)^2 \\ \\ \Rightarrow\sigma' & =\sigma(1-\sigma) \end{aligned} dxdσ(x)⇒σ′=dxd(1+e−x1)=(1+e−x)2e−x=(1+e−x)2(1+e−x)−1=(1+e−x)21+e−x−(1+e−x1)2=σ(x)−σ(x)2=σ(1−σ)所以对Sigmoid函数求导是非常简单的。但是 Sigmoid函数有一个最致命的缺陷:当输入值趋近于负无穷或者正无穷时,导数值趋近于0,会发生梯度弥散,参数无法更新。
PyTorch API:torch.sigmoid() 或 torch.sigmoid_() 或 F.sigmoid()
同样的,使用torch.sigmoid()需要再次进行赋值,而 torch.sigmoid_() 会对原张量尽心修改,无需再次进行赋值。
In [2]: a = torch.linspace(-100, 100, 10)
In [3]: torch.sigmoid(a)
Out[3]:
tensor([0.0000e+00, 1.6655e-34, 7.4564e-25, 3.3382e-15, 1.4945e-05, 9.9999e-01,
1.0000e+00, 1.0000e+00, 1.0000e+00, 1.0000e+00])
In [4]: a
Out[4]:
tensor([-100.0000, -77.7778, -55.5556, -33.3333, -11.1111, 11.1111,
33.3333, 55.5556, 77.7778, 100.0000])
关于F.sigmoid():
from torch.nn import functional as F
F.sigmoid(a)
# 注意:warnings.warn("nn.functional.sigmoid is deprecated. Use torch.sigmoid instead.")
Tanh
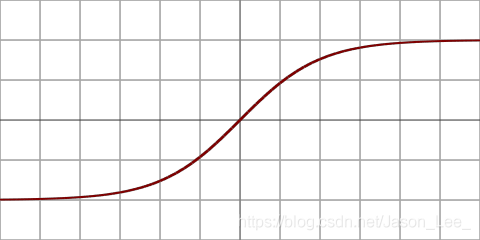
Tanh 在RNN中用的比较多,其表达式如下: f ( x ) = t a n h ( x ) = e x − e − x e x + e − x = 2 ∗ sigmoid ( 2 x ) − 1 ∈ ( − 1 , 1 ) f(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2*\text{sigmoid}(2x)-1\in(-1,1) f(x)=tanh(x)=ex+e−xex−e−x=2∗sigmoid(2x)−1∈(−1,1)函数曲线:
PyTorch API:torch.tanh() 或 torch.tanh() 或 F.tanh (nn.functional.tanh is deprecated.)
同样的,使用torch.tanh()需要再次进行赋值,而 torch.tanh_() 会对原张量尽心修改,无需再次进行赋值。
In [9]: a = torch.linspace(-1, 1, 10)
In [10]: torch.tanh(a)
Out[10]:
tensor([-0.7616, -0.6514, -0.5047, -0.3215, -0.1107, 0.1107, 0.3215, 0.5047, 0.6514, 0.7616])
In [11]: a
Out[11]:
tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556, 0.7778, 1.0000])
ReLU
修正线性单元(Rectified Linear Unit,ReLU)函数,该激活函数是现在神经网络中应用最广的激活函数,其性质决定了其特别适合于深度学习,很少出现梯度弥散和梯度爆炸的情况。其表达式如下: f ( x ) = { 0 for x < 0 x for x ≥ 0 f(x)=\begin{cases}0 &\text{for }x<0 \\ x &\text{for }x≥0 \end{cases} f(x)={ 0xfor x<0for x≥0函数曲线:

其导数: f ′ ( x ) = { 0 for x < 0 1 for x ≥ 0 f'(x)=\begin{cases}0 &\text{for }x<0 \\ 1 &\text{for }x≥0 \end{cases} f′(x)={ 01for x<0for x≥0
PyTorch API
torch.nn.functional.relu(input=Tensor, inplace=bool)
关于其中的 inplace=bool 参数:该参数用于指定是否将输出值覆盖掉输入值,该参数默认为 False ,如果设置为 True ,则覆盖掉,可以节约内存。举个栗子:
In [24]: import torch
In [25]: import torch.nn.functional as F
In [26]: a = torch.randn(3, 3)
In [27]: b = F.relu(a, inplace=False)
In [28]: a
Out[28]:
tensor([[-2.0796, 0.1338, 1.1616],
[ 0.4556, -0.2174, 1.2848],
[-0.7775, -0.0497, -0.0320]])
In [29]: b
Out[29]:
tensor([[0.0000, 0.1338, 1.1616],
[0.4556, 0.0000, 1.2848],
[0.0000, 0.0000, 0.0000]])
In [30]: id(a), id(b)
Out[30]: (140480473638224, 140480476648784)
In [31]: b = F.relu(a, inplace=True)
In [32]: a
Out[32]:
tensor([[0.0000, 0.1338, 1.1616],
[0.4556, 0.0000, 1.2848],
[0.0000, 0.0000, 0.0000]])
In [33]: b
Out[33]:
tensor([[0.0000, 0.1338, 1.1616],
[0.4556, 0.0000, 1.2848],
[0.0000, 0.0000, 0.0000]])
In [34]: id(a), id(b) # a, b 指向同一内存地址
Out[34]: (140480473638224, 140480473638224)
除非想要提取出中间变量,其余情况下,一般均将 replace 参数设置为 replace=True 。
其他的 PyTorch API:torch.relu() 或 torch.relu_() 或 F.relu()
In [19]: a = torch.linspace(-1, 1, 10)
In [20]: torch.relu(a)
Out[20]:
tensor([0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.1111, 0.3333, 0.5556, 0.7778,
1.0000])
In [21]: a
Out[21]:
tensor([-1.0000, -0.7778, -0.5556, -0.3333, -0.1111, 0.1111, 0.3333, 0.5556,
0.7778, 1.0000])
torch.nn.relu()与F.ReLU()辨析:- 类风格的 API :
类的命名风格为以大写字母开头,例如:nn.Linear()、nn.ReLU()等。
类风格的API需要先实例化,再调用。 - 函数风格的 API :
函数命名风格为 全部小写字母+下划线 组成,例如:F.cross_entropy()、F.relu()等。
- 类风格的 API :
Softmax
Softmax激活函数常与交叉熵(Cross Entropy,CE)损失函数搭配使用。二者常搭配起来用于分类问题。
Softmax可以将神经网络的输出转换为概率值,符合概率分布,并且可以将原始输出的大小差距变大 2 / 1 ⇒ 0.7 / 0.2 2/1\Rightarrow 0.7/0.2 2/1⇒0.7/0.2。
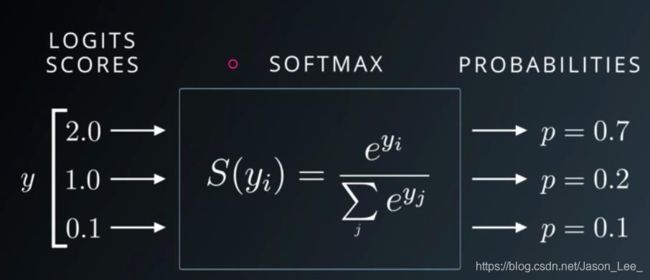
Softmax可以将网络的原始输出 y i y_i yi 变换为概率值 p i p_i pi ,Softmax 表达式: p i = e y i ∑ k = 1 n e y k p_i=\frac{e^{y_i}}{\sum_{k=1}^n e^{y_k}} pi=∑k=1neykeyi使用分式求导公式: f ( x ) g ( x ) ′ = f ′ ( x ) g ( x ) − f ( x ) g ′ ( x ) g ( x ) 2 \frac{f(x)}{g(x)}'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2} g(x)f(x)′=g(x)2f′(x)g(x)−f(x)g′(x) 求Softmax梯度: if i = j : ∂ p i ∂ y j = ∂ e y i ∑ k = 1 n e y k ∂ y j = e y i ∑ k = 1 N e y k − e y i e y j ( ∑ k = 1 N e y k ) 2 = e y i ∑ k = 1 N e y k − e y i ∗ e y j ( ∑ k = 1 N e y k ) 2 = p i − p i ∗ p j = p i ∗ ( 1 − p j ) \begin{aligned} \text{if }i=j:\frac{\partial p_i}{\partial y_j} & =\frac{\partial\frac{e^{y_i}}{\sum_{k=1}^ne^{y_k}}}{\partial y_j} \\ & =\frac{e^{y_i}\sum_{k=1}^N e^{y_k}-e^{y_i}e^{y_j}}{(\sum_{k=1}^Ne^{y_k})^2} \\ & =\frac{e^{y_i}}{\sum_{k=1}^Ne^{y_k}}-\frac{e^{y_i}*e^{y_j}}{(\sum_{k=1}^Ne^{y_k})^2} \\ & =p_i-p_i*p_j \\ & =p_i*(1-p_j) \end{aligned} if i=j:∂yj∂pi=∂yj∂∑k=1neykeyi=(∑k=1Neyk)2eyi∑k=1Neyk−eyieyj=∑k=1Neykeyi−(∑k=1Neyk)2eyi∗eyj=pi−pi∗pj=pi∗(1−pj)
if i ≠ j : ∂ p i ∂ y j = ∂ e y i ∑ k = 1 n e y k ∂ y j = 0 ∗ ∑ k = 1 N e y k − e y i e y j ( ∑ k = 1 N e y k ) 2 = − e y i ∑ k = 1 N e y k × e y j ∑ k = 1 N e y k = − p i ∗ p j \begin{aligned} \text{if }i\not =j:\frac{\partial p_i}{\partial y_j} & =\frac{\partial\frac{e^{y_i}}{\sum_{k=1}^ne^{y_k}}}{\partial y_j} \\ & =\frac{0*\sum_{k=1}^N e^{y_k}-e^{y_i}e^{y_j}}{(\sum_{k=1}^Ne^{y_k})^2} \\ & =-\frac{e^{y_i}}{\sum_{k=1}^Ne^{y_k}} \times \frac{e^{y_j}}{\sum_{k=1}^Ne^{y_k}} \\ & =-p_i*p_j \end{aligned} if i=j:∂yj∂pi=∂yj∂∑k=1neykeyi=(∑k=1Neyk)20∗∑k=1Neyk−eyieyj=−∑k=1Neykeyi×∑k=1Neykeyj=−pi∗pj综上,Softmax的梯度可以表示为: ∂ p i ∂ y j = { p i ( 1 − p j ) if i = j − p i ⋅ p j if i ≠ j \frac{\partial{p_i}}{\partial{y_j}}= \begin{cases} p_i(1-p_j) &\text{if }i=j \\ -p_i\cdot p_j &\text{if }i\not =j \end{cases} ∂yj∂pi={ pi(1−pj)−pi⋅pjif i=jif i=j还可以使用克罗内克函数(Kronecker delta): δ i j = { 1 if i = j 0 if i ≠ j \delta_{ij}= \begin{cases} 1 &\text{if }i=j \\ 0 &\text{if }i\not =j \end{cases} δij={ 10if i=jif i=j 来表示上述Softmax梯度: ∂ p i ∂ y j = p i ( δ i j − p j ) \frac{\partial{p_i}}{\partial{y_j}}=p_i(\delta_{ij}-p_j) ∂yj∂pi=pi(δij−pj)
PyTorch API:torch.nn.functional.softmax(Tensor, dim=) / F.softmax(Tensor, dim=) 或 torch.softmax(Tensor, dim=) dim参数必须指定,以确定对那个维度进行softmax操作,例如 shape=[batch_size, feature],需要设置dim=1。
In [3]: a = torch.rand(3)
In [4]: a.requires_grad_()
Out[4]: tensor([0.9451, 0.2082, 0.4011], requires_grad=True)
In [5]: p = F.softmax(a, dim=0)
In [6]: p.backward()
"""
RuntimeError: grad can be implicitly created only for scalar outputs
因为 p.shape = torch.Size([3]),而无论是使用 p.backward() 还是使用
torch.autograd.grad(p, [a]) 计算梯度,都要求 p 的 shape=0或者[1]。
"""
In [7]: torch.autograd.grad(p[0], [a], retain_graph=True)
Out[7]: (tensor([ 0.2498, -0.1129, -0.1369]),) # 由输出结果也可以看出,当 i=j 时,梯度为+,当 i≠j 时,梯度为-。
In [8]: torch.autograd.grad(p[2], [a])
Out[8]: (tensor([-0.1369, -0.0655, 0.2024]),)
In [9]: torch.autograd.grad(p[1], [a])
"""
RuntimeError: Trying to backward through the graph a second time, but the buffers have
already been freed. Specify retain_graph=True when calling backward the first time.
由于 torch.autograd.grad(p[2], [a]) 中未设置 retain_graph=True ,在执行完该语句后,计算梯度的计算图被释放,再次使用时会报错。
"""
7.4 Loss的梯度
经典损失函数:
- Mean Squared Error,MSE
- Cross Entropy,CE
- binary
- multi-class
- +softmax
交叉熵损失函数常与softmax激活函数结合使用 - 在第 8 章Logistic Regression 部分会对交叉熵进行详细讲解
Mean Squared Error,MSE
注意 MSE 与 L2 Norm 之间的区别:
- m s e = ∑ [ y − ( x w + b ) ] 2 mse=\sum[y-(xw+b)]^2 mse=∑[y−(xw+b)]2
- L 2 = ∥ y − ( x w + b ) ∥ 2 = ∑ ( y − ( x w + b ) ) 2 L_2=\|y-(xw+b)\|_2=\sqrt{\sum(y-(xw+b))^2} L2=∥y−(xw+b)∥2=∑(y−(xw+b))2
- m s e = L 2 2 mse=L_2^2 mse=L22
在PyTorch中利用 L2 Norm 实现 MSE :mse = torch.norm(y - y_pred, 2).pow(2)
MSE 梯度计算: l o s s = ∑ ( y − f θ ( x ) ) 2 ∇ l o s s ∇ θ = 2 ∗ ∑ ( y − f θ ( x ) ) ∗ ∇ f θ ( x ) ∇ θ \begin{aligned} & loss=\sum(y-f_\theta(x))^2 \\ & \frac{\nabla loss}{\nabla\theta}=2*\sum(y-f_\theta(x))*\frac{\nabla f_\theta(x)}{\nabla\theta} \end{aligned} loss=∑(y−fθ(x))2∇θ∇loss=2∗∑(y−fθ(x))∗∇θ∇fθ(x)其中, y p r e d = ∇ f θ ( x ) ∇ θ y_{pred}=\frac{\nabla f_\theta(x)}{\nabla\theta} ypred=∇θ∇fθ(x)取决于具体的网络结构。例如之前介绍的感知机函数: f ( x ) = w ∗ x + b ∇ f θ ( x ) ∇ θ = ∇ ( w , b ) = ( x , 1 ) \begin{aligned} & f(x)=w*x+b \\ \\ & \frac{\nabla f_\theta(x)}{\nabla\theta}=\nabla_{(w,b)}=(x, 1) \end{aligned} f(x)=w∗x+b∇θ∇fθ(x)=∇(w,b)=(x,1)
Cross Entropy,CE
交叉熵(Cross Entropy,CE)损失函数常与Softmax激活函数搭配使用。
在第 8 章8.2节部分会对交叉熵进行详细讲解。
7.5 单层感知机(Perception)的梯度计算与参数更新
在之前几节中介绍了常见的激活函数及Loss函数的梯度计算,在本节中,进行一个完整的多层神经网络的梯度推导过程。
单层单输出感知机梯度计算及参数更新过程
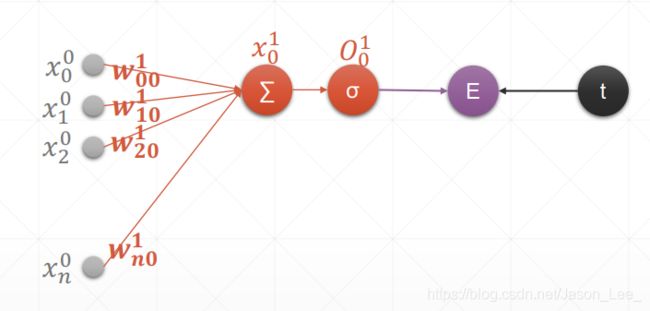
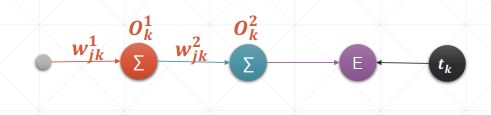
单层感知机的表达式: y = a c t i ( X W + b ) = a c t i ( ∑ k = 1 n x i k ∗ w k j + b ) \begin{aligned} y & =acti(XW+b) \\ & =acti(\sum_{k=1}^n x_{ik}*w_{kj}+b) \end{aligned} y=acti(XW+b)=acti(k=1∑nxik∗wkj+b)其中, i = 1 ; k = 1 , . . . , n ; j = 1 i=1; k=1,...,n; j=1 i=1;k=1,...,n;j=1 表示第一层输入层节点数为 X : 1 × n X: 1\times n X:1×n ,权重维度为 W : n × 1 W: n\times 1 W:n×1,输出节点数为 1 1 1。其模型示意图如下:

传统的单层感知机的激活函数一般使用阶跃函数,但是阶跃函数无法求导,所以此处我们使用sigmoid激活函数。
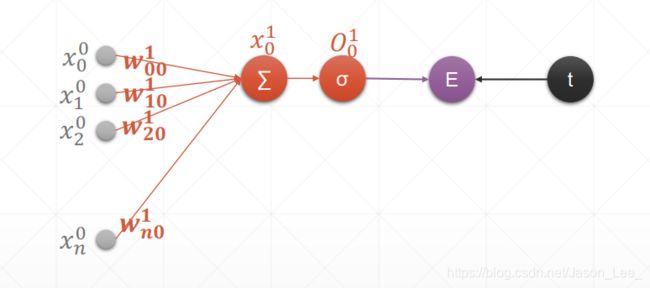
上图中, x i 0 x_i^0 xi0 表示第0层输入层的第 i i i 个节点, x 0 1 x_0^1 x01 表示第1层隐含层的输出的第0个节点, w i j 1 w_{ij}^1 wij1 表示第1层隐含层中的权重连接了上一层的第 i i i 个节点与下一层的第 j j j 个节点。
定义损失函数为MSE: l o s s = 1 2 ( O 0 1 − t ) 2 loss = \frac{1}{2}(O_0^1-t)^2 loss=21(O01−t)2,其中,t表示target(即label),1/2是为了计算方便人为加入的。计算梯度: l o s s = 1 2 ( O 0 1 − t ) 2 ∂ l o s s ∂ w j 0 1 = ( O 0 − t ) ∂ O 0 ∂ w j 0 1 = ( O 0 − t ) ∂ σ ( x 0 ) ∂ w j 0 1 = ( O 0 − t ) σ ( x 0 ) ( 1 − σ ( x 0 ) ) ∂ x 0 1 ∂ w j 0 1 = ( O 0 − t ) O 0 ( 1 − O 0 ) ∂ x 0 1 ∂ w j 0 1 = ( O 0 − t ) O 0 ( 1 − O 0 ) ∂ ( ∑ k = 1 n x k 0 ∗ w k 0 1 + b ) ∂ w j 0 1 = ( O 0 − t ) O 0 ( 1 − O 0 ) x j 0 \begin{aligned} loss & = \frac{1}{2}(O_0^1-t)^2 \\ \frac{\partial loss}{\partial w_{j0}^1} & =(O_0-t)\frac{\partial O_0}{\partial w_{j0}^1} \\ & =(O_0-t)\frac{\partial \sigma(x_0)}{\partial w_{j0}^1} \\ & =(O_0-t)\sigma(x_0)(1-\sigma(x_0))\frac{\partial x_0^1}{\partial w_{j0}^1} \\ & =(O_0-t)O_0(1-O_0)\frac{\partial x_0^1}{\partial w_{j0}^1} \\ & =(O_0-t)O_0(1-O_0)\frac{\partial (\sum_{k=1}^n x_{k}^0*w_{k0}^1+b)}{\partial w_{j0}^1} \\ & =(O_0-t)O_0(1-O_0)x_j^0 \end{aligned} loss∂wj01∂loss=21(O01−t)2=(O0−t)∂wj01∂O0=(O0−t)∂wj01∂σ(x0)=(O0−t)σ(x0)(1−σ(x0))∂wj01∂x01=(O0−t)O0(1−O0)∂wj01∂x01=(O0−t)O0(1−O0)∂wj01∂(∑k=1nxk0∗wk01+b)=(O0−t)O0(1−O0)xj0所以使用Sigmoid激活函数的单层感知机的梯度为: ∂ l o s s ∂ w j 1 = ( O 0 − t ) O 0 ( 1 − O 0 ) x j 0 \frac{\partial loss}{\partial w_j^1} =(O_0-t)O_0(1-O_0)x_j^0 ∂wj1∂loss=(O0−t)O0(1−O0)xj0在使用上式计算梯度之前,需要先进行前向传播,得到经过激活层后的输出 O 0 O_0 O0 。
PyTorch实现单层单输出感知机梯度计算及参数更新过程:
# 在本例中,我们同样设置偏置项 b=0
In [18]: x = torch.rand(1, 10)
In [19]: w = torch.rand(1, 10, requires_grad=True)
In [20]: o = torch.sigmoid(x@w.t()) # x 与 w 的转置 w.t() 进行矩阵乘法
In [21]: o.shape
Out[21]: torch.Size([1, 1])
In [22]: loss = F.mse_loss(torch.ones(1, 1), o)
In [23]: loss.shape # loss为一个标量,一次只能对一个损失函数进行反向传播计算梯度
Out[23]: torch.Size([])
In [24]: loss.backward()
In [25]: w.grad # 对w中共10个参数计算梯度
Out[25]:
tensor([[-0.0057, -0.0033, -0.0315, -0.0020, -0.0187, -0.0439, -0.0628, -0.0517, -0.0237, -0.0346]])
# 有了梯度信息,就可以使用参数更新公式更新参数了
In [26]: w
Out[26]:
tensor([[0.4177, 0.4392, 0.0890, 0.1062, 0.7068, 0.1003, 0.9056, 0.2665, 0.0495,
0.2354]], requires_grad=True)
In [27]: w - w.grad * 0.1 # 此处为了显示参数更新的效果,设置了较大的learning rate=0.1
Out[27]:
tensor([[0.4182, 0.4395, 0.0921, 0.1064, 0.7086, 0.1046, 0.9119, 0.2717, 0.0519, 0.2388]], grad_fn=<SubBackward0>)
单层多输出感知机梯度计算及参数更新过程
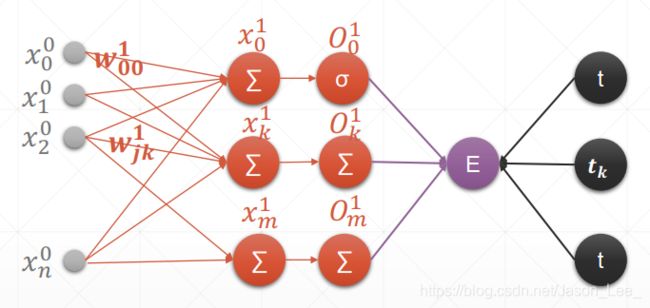
在上一节中,介绍了只有一个神经元的单输出感知机的梯度计算及梯度更新过程,接下来,将对具有多个神经元的单层神经网络——多输出感知机(Multi-output Perceptron)进行梯度计算及参数更新进行介绍。但是多输出感知机已经不是传统意义上的感知机了,传统的感知机就是只有一个输出的。多输出感知机更类似于深度学习中神经网络全连接层的结构。
下表展示了单输出感知机与多输出感知的对比:
输入层包含 N 个节点,第1层隐含层的输出层包含 M 个节点,即感知机有 M 个输出,对应于 M分类问题。
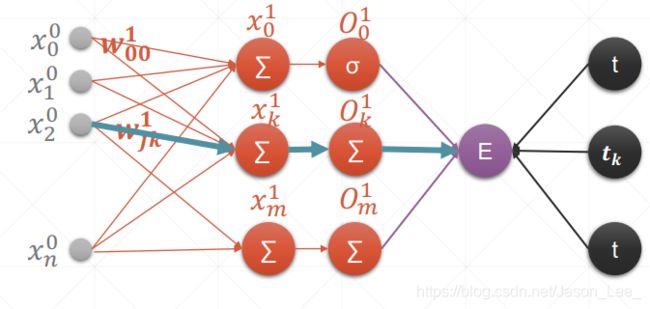
同样的,将损失函数定义为MSE: l o s s = 1 2 ( O i 1 − t i ) 2 loss = \frac{1}{2}(O_i^1-t_i)^2 loss=21(Oi1−ti)2,其中,t表示target(即label),1/2是为了计算方便人为加入的, O k O_k Ok 采用Sigmoid激活函数。计算梯度: l o s s = 1 2 ( O i 1 − t i ) 2 ∂ l o s s ∂ w j k 1 = ( O k 1 − t k ) ∂ O k 1 ∂ w j k 1 = ( O k 1 − t k ) ∂ σ ( x k 1 ) ∂ w j k 1 = ( O k 1 − t k ) σ ( x k 1 ) ( 1 − σ ( x k 1 ) ) ∂ x k 1 ∂ w j k 1 = ( O k 1 − t k ) O k 1 ( 1 − O k 1 ) ∂ x k 1 ∂ w j k 1 = ( O k 1 − t k ) O k 1 ( 1 − O k 1 ) ∂ ( ∑ i = 1 n x i 0 ∗ w i k 1 + b ) ∂ w j k 1 = ( O k 1 − t k ) O k 1 ( 1 − O k 1 ) x j 0 \begin{aligned} loss & = \frac{1}{2}(O_i^1-t_i)^2 \\ \frac{\partial loss}{\partial w_{jk}^1} & =(O_k^1-t_k)\frac{\partial O_k^1}{\partial w_{jk}^1} \\ & =(O_k^1-t_k)\frac{\partial \sigma(x_k^1)}{\partial w_{jk}^1} \\ & =(O_k^1-t_k)\sigma(x_k^1)(1-\sigma(x_k^1))\frac{\partial x_k^1}{\partial w_{jk}^1} \\ & =(O_k^1-t_k)O_k^1(1-O_k^1)\frac{\partial x_k^1}{\partial w_{jk}^1} \\ & =(O_k^1-t_k)O_k^1(1-O_k^1)\frac{\partial (\sum_{i=1}^n x_{i}^0*w_{ik}^1+b)}{\partial w_{jk}^1} \\ & =(O_k^1-t_k)O_k^1(1-O_k^1)x_j^0 \end{aligned} loss∂wjk1∂loss=21(Oi1−ti)2=(Ok1−tk)∂wjk1∂Ok1=(Ok1−tk)∂wjk1∂σ(xk1)=(Ok1−tk)σ(xk1)(1−σ(xk1))∂wjk1∂xk1=(Ok1−tk)Ok1(1−Ok1)∂wjk1∂xk1=(Ok1−tk)Ok1(1−Ok1)∂wjk1∂(∑i=1nxi0∗wik1+b)=(Ok1−tk)Ok1(1−Ok1)xj0所以使用Sigmoid激活函数的单层多输出感知机的梯度为: ∂ l o s s ∂ w j k 1 = ( O k 1 − t k ) O k 1 ( 1 − O k 1 ) x j 0 , ( j = 1 , 2 , . . . , N ; k = 1 , 2 , . . . , M ) \frac{\partial loss}{\partial w_{jk}^1} =(O_k^1-t_k)O_k^1(1-O_k^1)x_j^0,(j=1,2,...,N;k=1,2,...,M) ∂wjk1∂loss=(Ok1−tk)Ok1(1−Ok1)xj0,(j=1,2,...,N;k=1,2,...,M)在使用上式计算梯度之前,需要先进行前向传播,得到经过激活层后的输出 O k 1 , k = 1 , 2 , . . . , M O_k^1, k=1, 2, ...,M Ok1,k=1,2,...,M 。
PyTorch实现单层多输出感知机梯度计算及参数更新过程:
In [8]: x = torch.randn(1, 10)
In [9]: w = torch.randn(3, 10, requires_grad=True)
In [10]: o = torch.sigmoid(x@w.t())
In [11]: o.shape
Out[11]: torch.Size([1, 3])
In [12]: loss = F.mse_loss(torch.ones(1, 1), o)
"""
UserWarning: Using a target size (torch.Size([1, 3])) that is different to the input size (torch.Size([1, 1])).
This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
当label与pred维度不一致时,符合Broadcasting原则时会自动进行Broadcasting操作,但是会输出一个提示。
"""
In [13]: loss = F.mse_loss(torch.ones(1, 3), o)
In [14]: loss.backward()
In [15]: w.grad # w中共包含30个参数
Out[15]:
tensor([[-0.0744, -0.0926, 0.0379, -0.0412, 0.0010, 0.0157, 0.0420, -0.1026, 0.0687, -0.0309],
[-0.0191, -0.0237, 0.0097, -0.0106, 0.0003, 0.0040, 0.0108, -0.0263, 0.0176, -0.0079],
[-0.0387, -0.0481, 0.0197, -0.0214, 0.0005, 0.0082, 0.0218, -0.0533, 0.0357, -0.0161]])
In [16]: w - w.grad * 0.1 # 使用参数更新公式进行参数更新
7.6 链式法则
深度学习中最重要的公式之一:链式法则。链式法则是微积分中的求导法则,用于求一个复合函数的导数。复合函数的导数将是构成复合这有限个函数在相应点的导数的乘积,就像锁链一样一环套一环,故称链式法则。通过链式法则,就可以将神经网络最后一层的误差逐层输出至中间层,从而得到中间层的梯度信息,进而更新中间层的参数值。
求导法则:
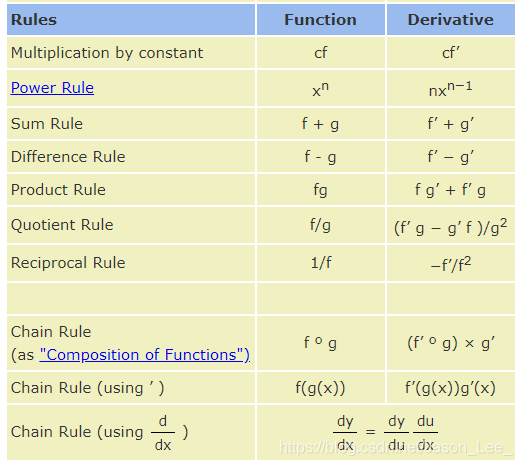
链式法则: ∂ y ∂ x = ∂ y ∂ u ∂ u ∂ x \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x} ∂x∂y=∂u∂y∂x∂u对于神经网络中前向传播过程: y 1 = x w 1 + b 1 y 2 = y 1 w 2 + b 2 \begin{aligned} & y_1=xw_1+b_1 \\ & y_2=y_1w_2+b_2 \end{aligned} y1=xw1+b1y2=y1w2+b2使用链式法则求导 ∂ y 2 ∂ w 1 \frac{\partial y_2}{\partial w_1} ∂w1∂y2 : ∂ y 2 ∂ w 1 = ∂ f ( y 1 ) ∂ w 1 = ∂ f ( y 1 ) ∂ y 1 ∂ y 1 ∂ w 1 = w 2 ∗ x \begin{aligned} \frac{\partial y_2}{\partial w_1} & =\frac{\partial f(y_1)}{\partial w_1} \\ & =\frac{\partial f(y_1)}{\partial y_1} \frac{\partial y_1}{\partial w_1} \\ & =w_2*x \end{aligned} ∂w1∂y2=∂w1∂f(y1)=∂y1∂f(y1)∂w1∂y1=w2∗x下图为一个神经网络简化后的示意图:
对这个真实的神经网络进行链式求导: ∂ E ∂ w j k 1 = ∂ E ∂ O k 1 ∂ O k 1 ∂ w j k 1 = ∂ E ∂ O k 2 ∂ O k 2 ∂ O k 1 ∂ O k 1 ∂ w j k 1 \frac{\partial E}{\partial w_{jk}^1}=\frac{\partial E}{\partial O_k^1}\frac{\partial O_k^1}{\partial w_{jk}^1}=\frac{\partial E}{\partial O_{k}^2}\frac{\partial O_k^2}{\partial O_{k}^1}\frac{\partial O_k^1}{\partial w_{jk}^1} ∂wjk1∂E=∂Ok1∂E∂wjk1∂Ok1=∂Ok2∂E∂Ok1∂Ok2∂wjk1∂Ok1
PyTorch实现链式法则求梯度:
In [6]: x = torch.tensor(1.)
In [7]: w1 = torch.tensor(2., requires_grad=True)
In [8]: b1 = torch.tensor(1.)
In [9]: w2 = torch.tensor(2., requires_grad=True)
In [10]: b2 = torch.tensor(1.)
In [11]: y1 = x*w1 + b1
In [12]: y2 = y1*w2 + b2
In [13]: dy2_dy1 = torch.autograd.grad(y2, [y1], retain_graph=True)
In [14]: dy2_dy1
Out[14]: (tensor(2.),)
In [15]: dy1_dw1 = torch.autograd.grad(y1, [w1], retain_graph=True)
In [16]: dy2_dw1 = torch.autograd.grad(y2, [w1], retain_graph=True)
In [17]: dy2_dy1 * dy1_dw1
"""
TypeError: can't multiply sequence by non-int of type 'tuple'
torch.autograd.grad()返回的是一个元组tuple类型的张量,不能直接进行乘法操作。
"""
In [18]: dy2_dy1 = torch.autograd.grad(y2, [y1], retain_graph=True)[0]
In [19]: dy1_dw1 = torch.autograd.grad(y1, [w1], retain_graph=True)[0]
In [20]: dy2_dw1 = torch.autograd.grad(y2, [w1], retain_graph=True)[0]
In [21]: dy2_dy1 * dy1_dw1
Out[21]: tensor(2.)
In [22]: dy2_dw1
Out[22]: tensor(2.)
7.7 多层感知机(MLP)反向传播算法
本节将介绍一个完整的多层感知机(multilayer perceptron, MLP)的反向传播过程。在这之前,先回顾一下单层单输出感知机和单层多输出感知机(Multi-output Perceptron)的梯度计算以及链式法则的计算过程:
结合单层多输出感知机和链式法则,就可以得到多层多输出感知机的模型:

上图中蓝色部分即为相比于单层多输出感知机模型增加的 多个隐含层 部分。
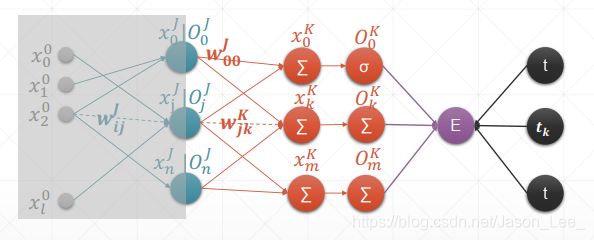
将上图灰色部分遮挡,剩余的部分和单层多输出感知机的结构相同。
注意: 下述梯度计算过程只针对上图中的虚线路径。
设置损失函数为MSE: l o s s = 1 2 ( O k K − t k ) 2 loss = \frac{1}{2}(O_k^K-t_k)^2 loss=21(OkK−tk)2,其中,t表示target(即label),1/2是为了计算方便人为加入的, O k O_k Ok 采用Sigmoid激活函数。
对神经网络最后一层进行梯度计算:
那么,由单层多输出感知机的梯度计算公式可以得到多层多输出感知机 最后一层 的梯度计算公式: ∂ l o s s ∂ w j k 1 = ( O k 1 − t k ) O k 1 ( 1 − O k 1 ) x j 0 ⇒ M L P 最 后 一 层 梯 度 计 算 ∂ l o s s ∂ w j k K = ( O k K − t k ) O k K ( 1 − O k K ) O j J \begin{aligned} & \frac{\partial loss}{\partial w_{jk}^1} =(O_k^1-t_k)O_k^1(1-O_k^1)x_j^0 \\ \xRightarrow{MLP最后一层梯度计算}& \frac{\partial loss}{\partial w_{jk}^K} =(O_k^K-t_k)O_k^K(1-O_k^K)O_j^J \end{aligned} MLP最后一层梯度计算∂wjk1∂loss=(Ok1−tk)Ok1(1−Ok1)xj0∂wjkK∂loss=(OkK−tk)OkK(1−OkK)OjJ
上述的 MLP 最后一层梯度计算公式是最终的 l o s s loss loss 关于输入 O j J O_j^J OjJ 的函数, O k K O_k^K OkK 为常数,所以令 ( O k K − t k ) O k K ( 1 − O k K ) = 记 为 μ k K (O_k^K-t_k)O_k^K(1-O_k^K)\xlongequal{记为}\mu_k^K (OkK−tk)OkK(1−OkK)记为μkK ,将最后一层的梯度计算公式简化为: ∂ l o s s ∂ w j k K = μ k K O j J ; ( j = 1 , 2 , . . . , N ; k = 1 , 2 , . . . , M ) \frac{\partial loss}{\partial w_{jk}^K}=\mu_k^KO_j^J;(j=1,2,...,N;k=1,2,...,M) ∂wjkK∂loss=μkKOjJ;(j=1,2,...,N;k=1,2,...,M)
根据上述公式可以计算得到神经网络第 K 层权重参数的梯度矩阵 G K = [ G j k K ] , G j k K = ∂ l o s s ∂ w j k K G^K=[G_{jk}^K],G_{jk}^K=\frac{\partial loss}{\partial w_{jk}^K} GK=[GjkK],GjkK=∂wjkK∂loss ,根据该矩阵即可使用参数更新公式对第 K 层权重参数进行更新。
对神经网络倒数第 2 层进行梯度计算:

依照上面对神经网络最后一层的梯度计算过程,可以对神经网络倒数第 2 层的梯度进行计算,即计算 ∂ l o s s ∂ W i j J \frac{\partial{loss}}{\partial{W_{ij}^J}} ∂WijJ∂loss : ∂ l o s s ∂ W i j J = ∂ ∂ W i j J ( 1 2 ∑ k = 1 M ( O k K − t k ) 2 ) = ∑ k = 1 M ( O k K − t k ) ∂ O k K ∂ w j k J = ∑ k = 1 M ( O k K − t k ) ∂ σ ( x k K ) ∂ w j k J = ∑ k = 1 M ( O k K − t k ) σ ( x k K ) ( 1 − σ ( x k K ) ) ∂ x k K ∂ w j k J ; (使用链式法则) = ∑ k = 1 M ( O k K − t k ) O k K ( 1 − O k K ) ∂ x k K ∂ O j J ∂ O j J ∂ w j k J ; ( 等 效 于 ∂ ( w j k K ∗ O j J + b k ) ∂ w j k J ) = ∑ k = 1 M ( O k K − t k ) O k K ( 1 − O k K ) w j k K ∂ ( O j J ) ∂ w j k J = ∑ k = 1 M ( O k K − t k ) O k K ( 1 − O k K ) w j k K ( O j J ( 1 − O j J ) ∂ x j J ∂ w j k J ) = ∑ k = 1 M ( O k K − t k ) O k K ( 1 − O k K ) w j k K ( O j J ( 1 − O j J ) ∂ ( w j k J ∗ O i I + b j ) ∂ w j k J ) ; ( 其 中 O i I 为 倒 数 第 3 层 的 输 出 ) = ∑ k = 1 M ( O k K − t k ) O k K ( 1 − O k K ) w j k K ( O j J ( 1 − O j J ) O i I ) = ( O i I O j J ( 1 − O j J ) ) ∑ k = 1 M μ k K w j k K = μ j J O i I \begin{aligned} \frac{\partial{loss}}{\partial{W_{ij}^J}} & = \frac{\partial{}}{\partial{W_{ij}^J}}\Big(\ \frac{1}{2} \sum_{k=1}^M (O_k^K-t_k)^2 \Big) \\ & =\sum_{k=1}^M (O_k^K-t_k)\frac{\partial{O_k^K}}{\partial{w_{jk}^J}} \\ & =\sum_{k=1}^M (O_k^K-t_k)\frac{\partial{\sigma(x_k^K)}}{\partial{w_{jk}^J}} \\ & =\sum_{k=1}^M (O_k^K-t_k) \sigma(x_k^K)(1-\sigma(x_k^K)) \frac{\partial{x_k^K}}{\partial{w_{jk}^J}} ; \text{ (使用链式法则)} \\ & =\sum_{k=1}^M (O_k^K-t_k) O_k^K(1-O_k^K) \frac{\partial{x_k^K}}{\partial{O_j^J}}\frac{\partial{O_j^J}}{\partial{w_{jk}^J}} ; (等效于\frac{\partial{(w_{jk}^K*O_j^J+b_k)}}{\partial{w_{jk}^J}}) \\ & =\sum_{k=1}^M (O_k^K-t_k) O_k^K(1-O_k^K) w_{jk}^K\frac{\partial{(O_j^J)}}{\partial{w_{jk}^J}} \\ & =\sum_{k=1}^M (O_k^K-t_k) O_k^K(1-O_k^K) w_{jk}^K\Bigg(O_j^J(1-O_j^J)\frac{\partial{x_j^J}}{\partial{w_{jk}^J}} \Bigg) \\ & =\sum_{k=1}^M (O_k^K-t_k) O_k^K(1-O_k^K) w_{jk}^K\Bigg(O_j^J(1-O_j^J)\frac{\partial{(w_{jk}^J*O_i^I+b_j)}}{\partial{w_{jk}^J}} \Bigg) ; (其中O_i^I为倒数第3层的输出) \\ & =\sum_{k=1}^M (O_k^K-t_k) O_k^K(1-O_k^K) w_{jk}^K\Bigg(O_j^J(1-O_j^J)O_i^I \Bigg) \\ & = \Bigg( O_i^I O_j^J(1-O_j^J) \Bigg)\sum_{k=1}^M \mu_k^K w_{jk}^K \\ & =\mu_j^J O_i^I \end{aligned} ∂WijJ∂loss=∂WijJ∂( 21k=1∑M(OkK−tk)2)=k=1∑M(OkK−tk)∂wjkJ∂OkK=k=1∑M(OkK−tk)∂wjkJ∂σ(xkK)=k=1∑M(OkK−tk)σ(xkK)(1−σ(xkK))∂wjkJ∂xkK; (使用链式法则)=k=1∑M(OkK−tk)OkK(1−OkK)∂OjJ∂xkK∂wjkJ∂OjJ;(等效于∂wjkJ∂(wjkK∗OjJ+bk))=k=1∑M(OkK−tk)OkK(1−OkK)wjkK∂wjkJ∂(OjJ)=k=1∑M(OkK−tk)OkK(1−OkK)wjkK(OjJ(1−OjJ)∂wjkJ∂xjJ)=k=1∑M(OkK−tk)OkK(1−OkK)wjkK(OjJ(1−OjJ)∂wjkJ∂(wjkJ∗OiI+bj));(其中OiI为倒数第3层的输出)=k=1∑M(OkK−tk)OkK(1−OkK)wjkK(OjJ(1−OjJ)OiI)=(OiIOjJ(1−OjJ))k=1∑MμkKwjkK=μjJOiI
根据上述公式可以计算得到神经网络第 J 层权重参数的梯度矩阵 G J = [ G j k J ] , G j k J = ∂ l o s s ∂ w j k J G^J=[G_{jk}^J],G_{jk}^J=\frac{\partial loss}{\partial w_{jk}^J} GJ=[GjkJ],GjkJ=∂wjkJ∂loss ,根据该矩阵即可使用参数更新公式对第 J 层权重参数进行更新。
现在对上述的过程进行一下总结:
可以归纳出对倒数第 3 层 I I I 的梯度计算公式为: ∂ l o s s ∂ W h i I = ( O i I − 1 O i I ( 1 − O i I ) ) ∑ j = 1 N μ j J w i j J ∂ l o s s ∂ W h i I = μ i I O i I − 1 \begin{aligned} & \frac{\partial{loss}}{\partial{W_{hi}^I}} =\Bigg( O_i^{I-1} O_i^I(1-O_i^I) \Bigg)\sum_{j=1}^N \mu_j^J w_{ij}^J \\ & \frac{\partial{loss}}{\partial{W_{hi}^I}}=\mu_i^IO_i^{I-1} \end{aligned} ∂WhiI∂loss=(OiI−1OiI(1−OiI))j=1∑NμjJwijJ∂WhiI∂loss=μiIOiI−1根据以上过程依次向前计算梯度,即可完成反向传播过程。
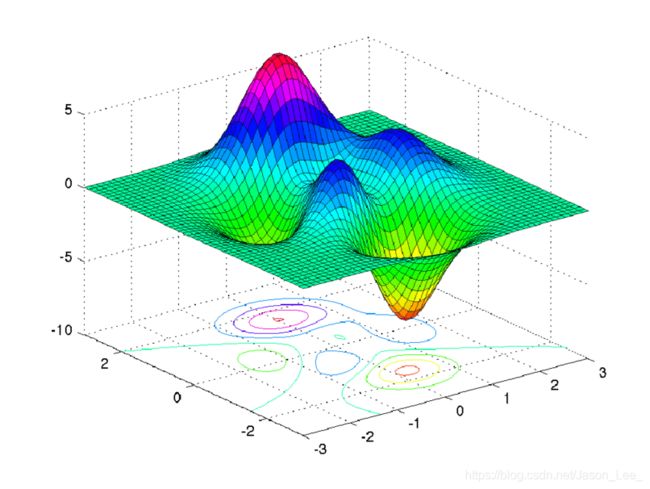
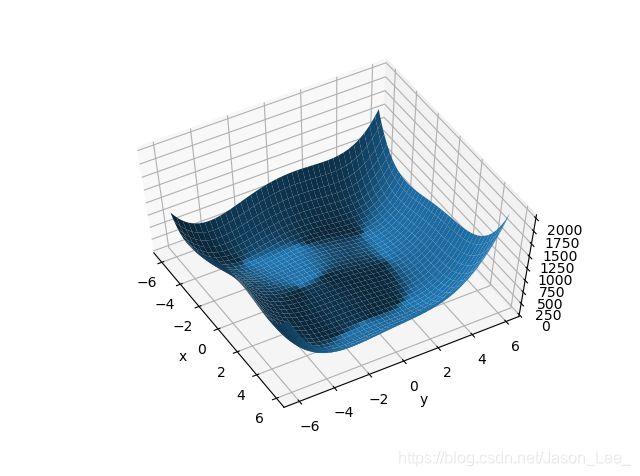
7.8 2D函数(Himmelblau function)优化问题实战
在数学优化中,Himmelblau function是一个多峰函数,常用于测试优化算法的性能。该函数定义为: f ( x , y ) = ( x 2 + y − 11 ) 2 + ( x + y 2 − 7 ) 2 f(x,y)=(x^2+y-11)^2+(x+y^2-7)^2 f(x,y)=(x2+y−11)2+(x+y2−7)2其包含 1 个局部最大值和 4 个全局最小值: f ( − 0.270845 , − 0.923039 ) = 181.617 f ( 3.0 , 2.0 ) = 0.0 f ( − 2.805118 , 3.131312 ) = 0.0 f ( − 3.779310 , − 3.283186 ) = 0.0 f ( 3.584428 , − 1.848126 ) = 0.0 \begin{aligned} & f(-0.270845,-0.923039)=181.617 \\ & f(3.0,2.0)=0.0 \\ & f(-2.805118,3.131312)=0.0 \\ & f(-3.779310,-3.283186)=0.0 \\ & f(3.584428,-1.848126)=0.0 \end{aligned} f(−0.270845,−0.923039)=181.617f(3.0,2.0)=0.0f(−2.805118,3.131312)=0.0f(−3.779310,−3.283186)=0.0f(3.584428,−1.848126)=0.0该函数已经求得了封闭解(closed-formed solution),所以可以用其来测试提出的优化器性能,看其是否能找到最优解。该函数曲面如下图所示:
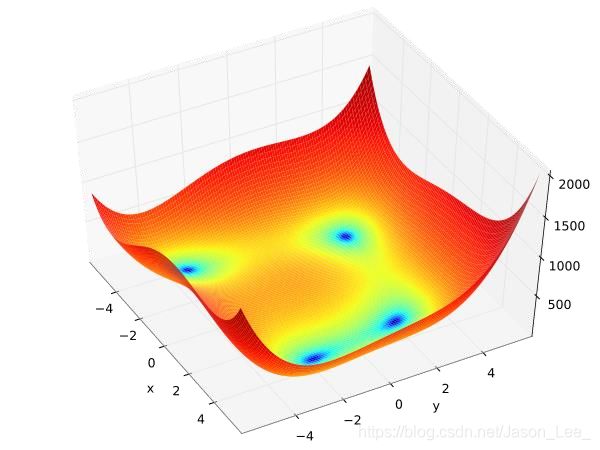 |
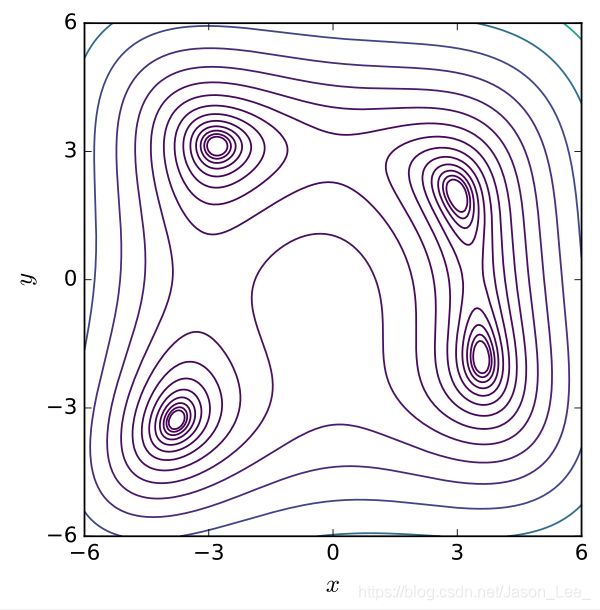 |
|---|
Himmelblau函数曲面绘制:
# 定义Himmelblau函数
def himmelblau(x):
return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape) # 输出:x,y range: (120,) (120,)
X, Y = np.meshgrid(x, y) # 用于生成网格点坐标矩阵。
print('X,Y maps:', X.shape, Y.shape) # 输出:X,Y maps: (120, 120) (120, 120)
Z = himmelblau([X, Y]) # 使用himmelblau函数求取坐标点处的函数值
# 绘制himmelblau函数曲面
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
绘图结果:
# 对himmelblau函数中的参数x进行优化
# [1., 0.], [-4, 0.], [4, 0.] 选择不同的初始化值,会得到不同的极小值点
x = torch.tensor([-4., 0.], requires_grad=True)
optimizer = torch.optim.Adam([x], lr=1e-3) # 指定优化器(待优化参数, 学习率)
for step in range(20000):
pred = himmelblau(x)
optimizer.zero_grad() # 在每轮迭代之前,都需要清除当前优化器中的所有梯度信息
pred.backward() # 反向传播计算梯度
optimizer.step() # 执行一步优化步骤(参数更新)
if step % 2000 == 0:
print('step {}: x = {}, f(x) = {}'.format(step, x.tolist(), pred.item()))
"""
PyTorch中的Tensor.tolist()方法可以直接将张量转换为列表形式,与list(Tensor)不同
list(x)
[tensor(-3.7793, grad_fn=), tensor(-3.2832, grad_fn=)]
x.tolist()
[-3.7793102264404297, -3.2831859588623047]
Tensor.item() 会返回当前张量中的值,但是注意一次只能返回一个值,需要使用x[1].item()
"""
# step 0: x = [-3.999000072479248, -0.0009999999310821295], f(x) = 146.0
# step 2000: x = [-3.526559829711914, -2.5002429485321045], f(x) = 19.4503231048584
# step 4000: x = [-3.777446746826172, -3.2777843475341797], f(x) = 0.0012130826944485307
# step 6000: x = [-3.7793045043945312, -3.283174753189087], f(x) = 5.636138666886836e-09
# step 8000: x = [-3.779308319091797, -3.28318190574646], f(x) = 7.248672773130238e-10
# step 10000: x = [-3.7793095111846924, -3.28318452835083], f(x) = 8.822098607197404e-11
# step 12000: x = [-3.7793102264404297, -3.2831854820251465], f(x) = 8.185452315956354e-12
# step 14000: x = [-3.7793102264404297, -3.2831859588623047], f(x) = 0.0
# step 16000: x = [-3.7793102264404297, -3.2831859588623047], f(x) = 0.0
# step 18000: x = [-3.7793102264404297, -3.2831859588623047], f(x) = 0.0
本文仅为笔者PyTorch学习笔记,部分图文来源于网络,若有侵权,联系即删。
Reference
https://study.163.com/course/introduction/1208894818.htm