140 - The 12th Zhejiang Provincial Collegiate Programming Contest（第二部分）

Floor Function

---

Time Limit: 10 Seconds       Memory Limit: 65536 KB

---

a, b, c and d are all positive integers which satisfy bc - ad > 0. Your task is to minimize the following function of a positive integer n.

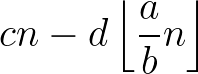
⌊x⌋, the floor function, means the largest integer not greater than x.

You need to find a positive integer n to minimize the above function. If there are multiple n's minimizing it, find the smallest one.

Input

There are multiple test cases. The first line of input contains an integer T ≈ 100000 indicating the number of test cases. For each test case:

There are four positive integers: a, b, c and d. (1 <= a, b, c, d <= 10¹⁸)

Output

For each case, print the smallest positive integer n which minimizes the function.

Sample Input

3

1 2 3 4

3 4 4 5

97 37 101 31

Sample Output

2

4

1


题意：求最小的n使得等式结果最小
待更新....
转载请注明出处：寻找&星空の孩子

Permutation Graph

---

Time Limit: 3 Seconds       Memory Limit: 65536 KB

---

Edward has a permutation {a₁, a₂, … a_n}. He finds that if he connects each pair (a_i, a_j) such that i < j and a_i > a_j, he will get a graph.

For example, if the permutation is {2, 3, 1, 4}, then 1 and 2 are connected and 1 and 3 are connected.

Edward lost his permutation, but he does know the connected components of the corresponding graph. He wants to know how many permutations will result in the same connected components.

Note that two vertices u, v belong to the same connected component if there exists a sequence of vertices starting with u and ending with v such that every two subsequent vertices in the sequence are connected by an edge.

Input

There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case:

The first line contains two integers n, m (1 ≤ m ≤ n ≤ 100000), indicating the length of the permutation and the number of connected components in the graph.

Each of the following m lines contains an integer c_i which denotes the size of i-th connected component, followed by c_i distinct integers v_i,1, v_i,2, … v_i,ci which denotes the connected component (1 ≤ c_i, v_i,1, v_i,2, … v_i,ci≤ n).

It is guaranteed that every number will appear in exact one connected component and c₁ + c₂ + … + c_m = n.

Output

For each case, output the answer modulo 786433.

Sample Input

2

4 4

1 1

1 2

1 3

1 4

4 2

3 1 2 3

1 4

Sample Output

1

3

Hint

For the second case, the three permutations is: {2, 3, 1, 4}, {3, 2, 1, 4}, {3, 1, 2, 4}.

题意：每个集合里，每个大数可以把后面的小数连起来，问你全部能连起来的组合个数；
待更新...

转载请注明出处：寻找&星空の孩子

Lunch Time

---

Time Limit: 2 Seconds       Memory Limit: 65536 KB

---

The 999th Zhejiang Provincial Collegiate Programming Contest will be held in Marjar University. The canteen of Marjar University is making preparations for this grand competition. The canteen provides a lunch set of three types: appetizer, main course and dessert. Each type has several dishes with different prices for choosing.

Edward is the headmaster of Marjar University. One day, to inspect the quality of dishes, he go to the canteen and decides to choose a median set for his lunch. That means he must choose one dish from each of appetizers, main courses and desserts. Each chosen dish should at the median price among all dishes of the same type.

For example, if there are five dessert dishes selling at the price of 2, 3, 5, 10, 30, Edward should choose the dish with price 5 as his dessert since its price is located at the median place of the dessert type. If the number of dishes of a type is even, Edward will choose the dish which is more expensive among the two medians.

You are given the list of all dishes, please write a program to help Edward decide which dishes he should choose.

Input

There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case:

The first line contains three integers S, M and D (1 <= S, M, D <= 100), which means that there are S dishes of appetizer, M dishes of main course and D dishes of dessert.

Then followed by three parts. The first part contains S lines, the second and the last part contains M and D lines respectively. In each line of the three parts, there is a string and an integer indicating the name and the price of a dish. The name of dishes will only consist of non-whitespace characters with no more than 50 characters. The price of dishes are non-negative integers less than or equal to 1000. All dish names will be distinct.

Output

For each test case, output the total price of the median set, together with the names of appetizer, main course and dessert, separated by a single space.

Sample Input

2

1 3 2

Fresh_Cucumber 4

Chow_Mein 5

Rice_Served_with_Duck_Leg 12

Fried_Vermicelli 7

Steamed_Dumpling 3

Steamed_Stuffed_Bun 4

2 3 1

Stir-fried_Loofah_with_Dried_Bamboo_Shoot 33

West_Lake_Water_Shield_Soup 36

DongPo's_Braised_Pork 54

West_Lake_Fish_in_Vinegar 48

Longjing_Shrimp 188

DongPo's_Crisp 18

Sample Output

15 Fresh_Cucumber Fried_Vermicelli Steamed_Stuffed_Bun

108 West_Lake_Water_Shield_Soup DongPo's_Braised_Pork DongPo's_Crisp

题意：求每组甜点的中位数的和，如果有中位数有2组，取价格大的；

转载请注明出处：寻找&星空の孩子

#include <iostream>

#include <stdio.h>

#include <string.h>

#include <stack>

#include <queue>

#include <map>

#include <set>

#include <vector>

#include <math.h>

#include <algorithm>

using namespace std;

#define ls 2*i

#define rs 2*i+1

#define up(i,x,y) for(i=x;i<=y;i++)

#define down(i,x,y) for(i=x;i>=y;i--)

#define mem(a,x) memset(a,x,sizeof(a))

#define w(a) while(a)

#define LL long long

const double pi = acos(-1.0);

#define Len 20005

#define mod 19999997

const int INF = 0x3f3f3f3f;



int t,a,b,c;



struct node

{

    char name[105];

    int num;

}s[3][105];



int cmp(node a,node b)

{

    return a.num<b.num;

}



int main()

{

    int i,j,k;

    scanf("%d",&t);

    w(t--)

    {

        scanf("%d%d%d",&a,&b,&c);

        up(i,0,a-1)

        scanf("%s%d",s[0][i].name,&s[0][i].num);

        up(i,0,b-1)

        scanf("%s%d",s[1][i].name,&s[1][i].num);

        up(i,0,c-1)

        scanf("%s%d",s[2][i].name,&s[2][i].num);

        sort(s[0],s[0]+a,cmp);

        sort(s[1],s[1]+b,cmp);

        sort(s[2],s[2]+c,cmp);

        int ans=s[0][a/2].num+s[1][b/2].num+s[2][c/2].num;

        printf("%d %s %s %s\n",ans,s[0][a/2].name,s[1][b/2].name,s[2][c/2].name);

    }



    return 0;

}

 

 

May Day Holiday

---

Time Limit: 2 Seconds       Memory Limit: 65536 KB

---

As a university advocating self-learning and work-rest balance, Marjar University has so many days of rest, including holidays and weekends. Each weekend, which consists of Saturday and Sunday, is a rest time in the Marjar University.

The May Day, also known as International Workers' Day or International Labour Day, falls on May 1st. In Marjar University, the May Day holiday is a five-day vacation from May 1st to May 5th. Due to Saturday or Sunday may be adjacent to the May Day holiday, the continuous vacation may be as long as nine days in reality. For example, the May Day in 2015 is Friday so the continuous vacation is only 5 days (May 1st to May 5th). And the May Day in 2016 is Sunday so the continuous vacation is 6 days (April 30th to May 5th). In 2017, the May Day is Monday so the vacation is 9 days (April 29th to May 7th). How excited!

Edward, the headmaster of Marjar University, is very curious how long is the continuous vacation containing May Day in different years. Can you help him?

Input

There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case, there is an integer y (1928 <= y <= 9999) in one line, indicating the year of Edward's query.

Output

For each case, print the number of days of the continuous vacation in that year.

Sample Input

3

2015

2016

2017

Output

5

6

9

 题意：问五一放几天假，首先确定每年的五一在哪一天，因为周日到周六，都可以打表表示，所以确定闰年的个数就可以了，是闰年对应的星期就+2，其余的+1（相对与1928年）

转载请注明出处：寻找&星空の孩子

 

//1928年周二

#include<stdio.h>

int a[7]= {6,9,6,5,5,5,5};

int main()

{

    int year,T;

    scanf("%d",&T);

    while(T--)

    {

        scanf("%d",&year);

        int k=year-1928;

        int cnt=0;

        for(int i=1929; i<=year; i++)

        {

            if(i%400==0||(i%4==0&&i%100!=0)) cnt++;

        }

        printf("%d\n",a[(2+k+cnt)%7]);

    }

    return 0;

}