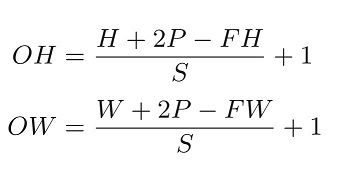CNN

一、卷积神经网络结构

1.全连接神经网络

基于全连接层（Affine 层）的网络

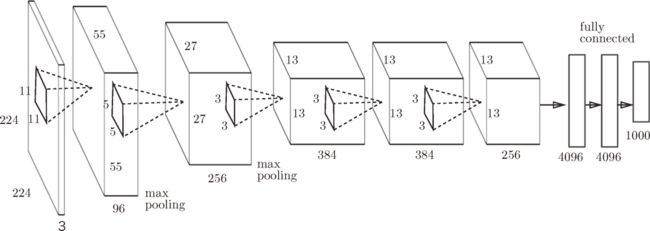
2.卷积神经网络

全连接层存在的问题：数据的形状被“忽视”了
例如，输入数据是图像时，图像通常是高、长、通道方向上的 3 维形状。但是，向全连接层输入时，需要将 3 维数据拉平为 1 维数据。实际上，前面提到的使用了 MNIST 数据集的例子中，输入图像就是 1 通道、高 28 像素、长 28 像素的（1, 28, 28）形状，但却被排成 1 列，以 784 个数据的形式输入到最开始的 Affine 层。
图像是 3 维形状，这个形状中应该含有重要的空间信息。例如，空间上邻近的像素为相似的值、RBG 的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等，3 维形状中可能隐藏有值得提取的本质模式。但是，因为全连接层会忽视形状，将全部的输入数据作为相同的神经元（同一维度的神经元）处理，所以无法利用与形状相关的信息。

而卷积层可以保持形状不变。当输入数据是图像时，卷积层会以 3 维数据的形式接收输入数据，并同样以 3 维数据的形式输出至下一层。因此，在 CNN 中，可以（有可能）正确理解图像等具有形状的数据。
CNN 中，有时将卷积层的输入输出数据称为特征图（feature map）。其中，卷积层的输入数据称为输入特征图（input feature map），输出数据称为输出特征图（output feature map）。

基于 CNN 的网络

二、卷积层

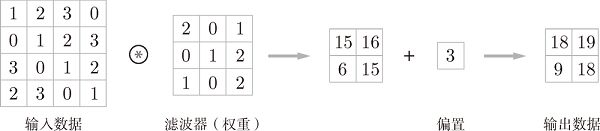
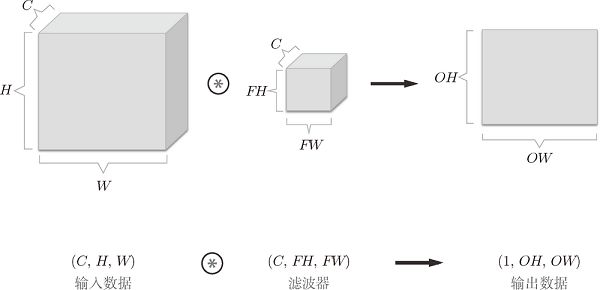
1.卷积运算（Convolution）

卷积运算

带偏置的卷积运算

2.填充（Padding）

在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（比如0等）。

幅度为 1 的填充（向输入数据的周围填入 0）

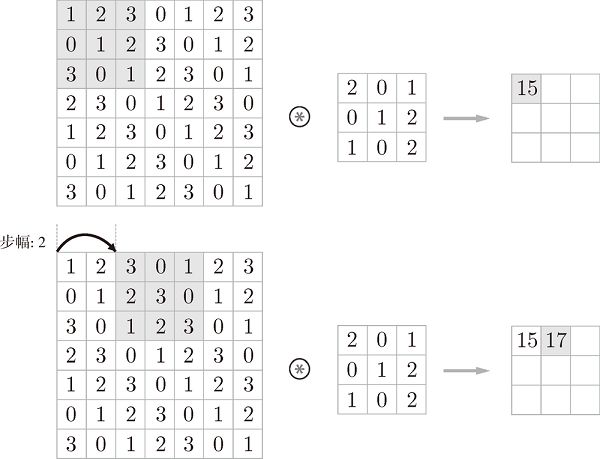
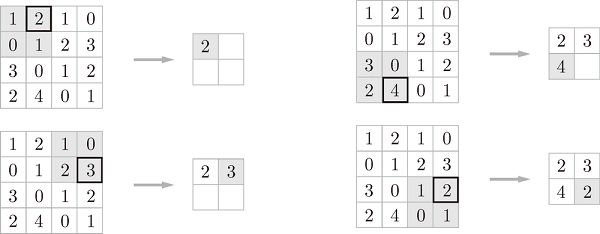
3.卷积步长（Stride）

应用滤波器的位置间隔称为步长（stride）。

步长为 2 的卷积运算

假设输入大小为 (H, W)，滤波器大小为 (FH, FW)，输出大小为 (OH, OW)，填充为 P，步幅为 S。此时，输出大小为

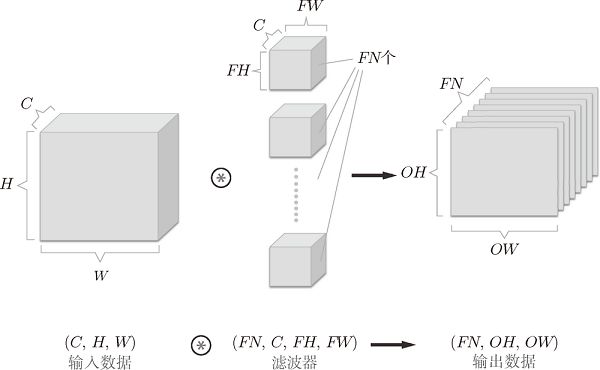
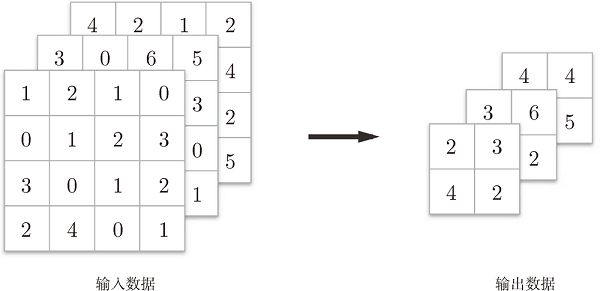
4.多通道卷积

通道方向上有多个特征图时，会按通道进行输入数据和滤波器的卷积运算，并将结果相加，从而得到输出。

通道数为C

多个滤波器

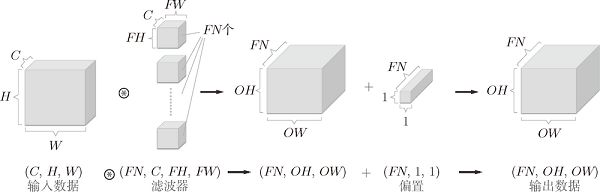
5.卷积层完整处理流

卷积层处理流

卷积层处理流（批处理）

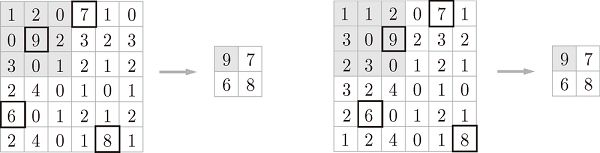
三、池化层

池化运算（ Max 池化）

除了 Max 池化之外，还有 Average 池化等。相对于 Max 池化是从目标区域中取出最大值，Average 池化则是计算目标区域的平均值。在图像识别领域，主要使用 Max 池化。

池化层的特征

1.没有要学习的参数

池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取最大值（或者平均值），所以不存在要学习的参数。

2.通道数不发生变化

经过池化运算，输入数据和输出数据的通道数不会发生变化。

通道数不变性

3.对微小的位置变化具有鲁棒性

输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对输入数据的微小偏差具有鲁棒性。

微小偏差鲁棒性

四、卷积层实现

1.基于 im2col 的展开

如果老老实实地实现卷积运算，估计要重复好几层的 for 语句。这样的实现有点麻烦，而且，NumPy 中存在使用 for 语句后处理变慢的缺点（NumPy 中，访问元素时最好不要用 for 语句）。这里，我们不使用 for 语句，而是使用 im2col 这个便利的函数进行简单的实现。

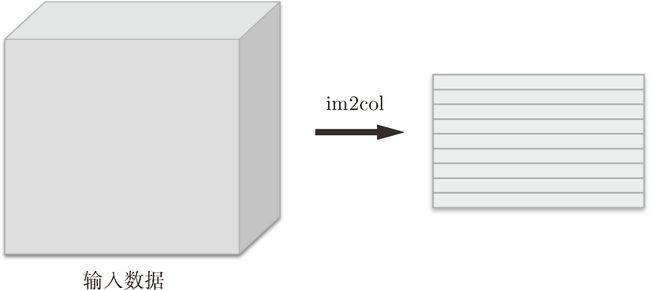
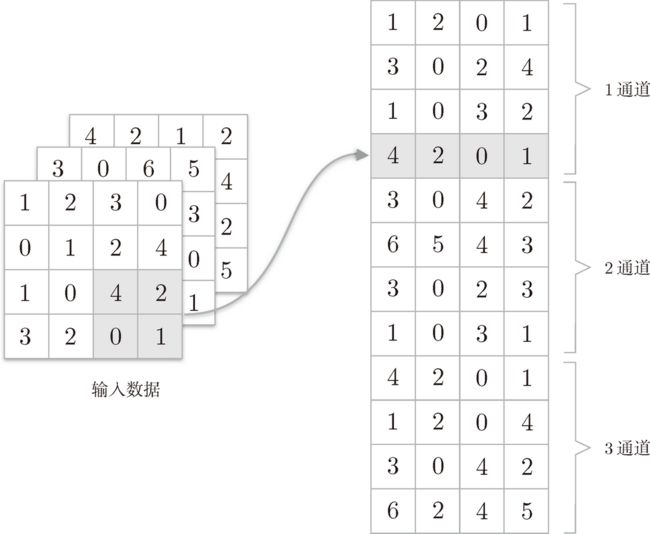
im2col 是一个函数，将输入数据展开以适合滤波器（权重）。如图 7-17 所示，对 3 维的输入数据应用 im2col 后，数据转换为 2 维矩阵（正确地讲，是把包含批数量的 4 维数据转换成了 2 维数据）。

将滤波器的应用区域从头开始依次横向展开为 1 列

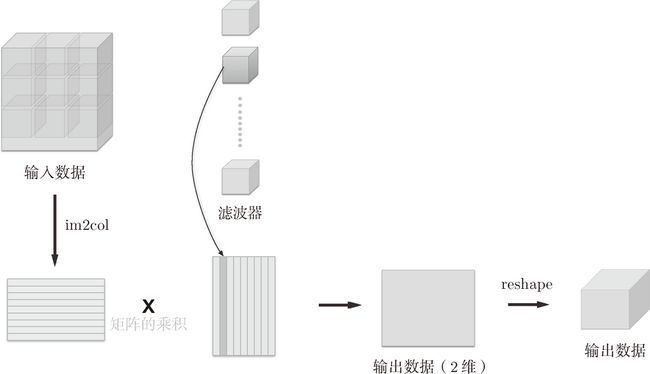
卷积运算的滤波器处理的细节：将滤波器纵向展开为 1 列，并计算和 im2col 展开的数据的矩阵乘积，最后转换（reshape）为输出数据的大小。

 class Convolution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad

    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
        out_w = int(1 + (W + 2*self.pad - FW) / self.stride)

        col = im2col(x, FH, FW, self.stride, self.pad)
        col_W = self.W.reshape(FN, -1).T # 滤波器的展开
        out = np.dot(col, col_W) + self.b

        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        return out

五、池化层实现

对输入数据展开池化的应用区域（2×2 的池化的例子）

池化层的实现流程：池化的应用区域内的最大值元素用灰色表示

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)

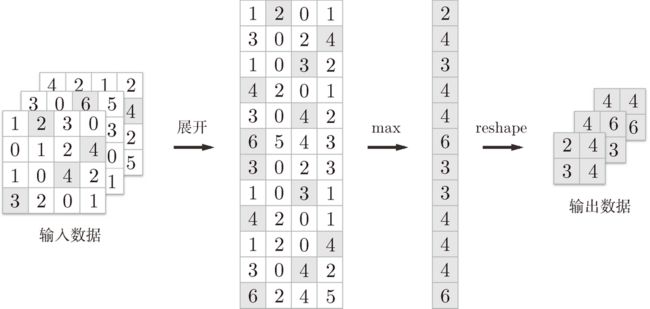
        # 展开(1)
        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
        col = col.reshape(-1, self.pool_h*self.pool_w)

        # 最大值(2)
        out = np.max(col, axis=1)
        # 转换(3)
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

        return out

六、常见构筑与算法

1.一维构筑

（1）时间延迟网络（Time Delay Neural Network, TDNN）

（2）WaveNet

2.二维构筑

（1）LeNet

（2）AlexNet

3.全卷积构筑

（1）SRCNN（Super Resolution CNN）

（2）U-Net

卷积神经网络

CNN