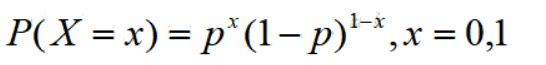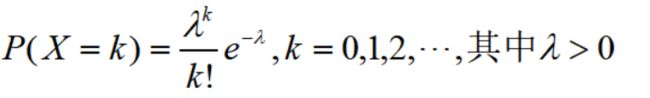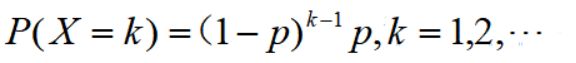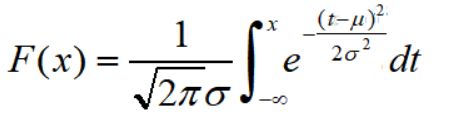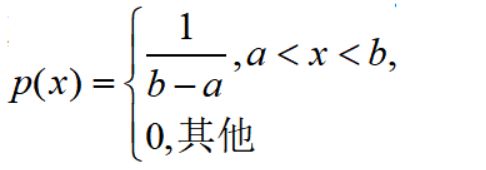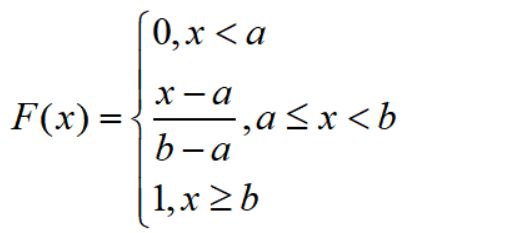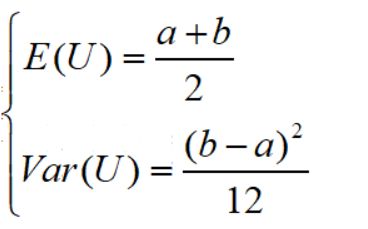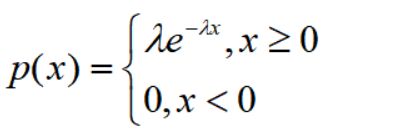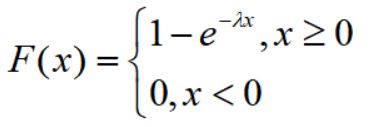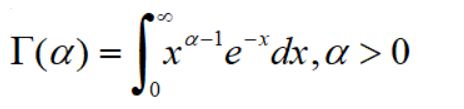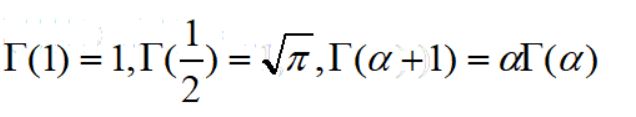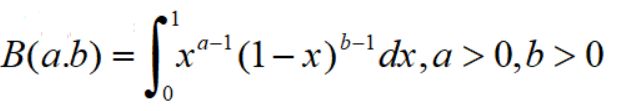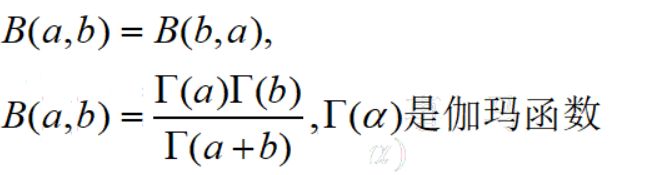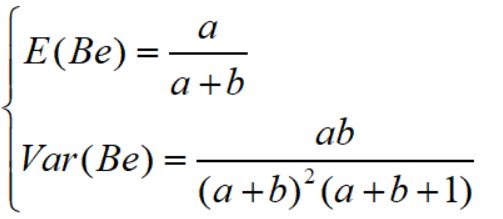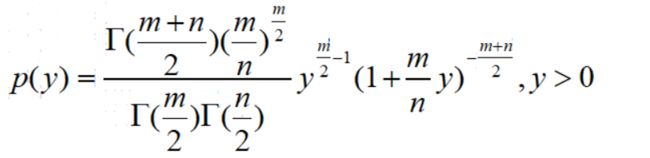十二种概率分布及python实现

1.常见离散分布有四种：二项分布、泊松分布、超几何分布和几何分布

2.常见连续分布有五种：正态分布、均匀分布、指数分布、伽玛分布和贝塔分布

3.三大抽样分布为：卡方分布、F分布和t分布

4.泊松分布的参数λ是单位时间或单位面积内随机事件的平均发生次数

5.指数分布的参数λ表示同一事件发生的平均时间间隔，它与泊松分布是相对的

6.当n<

7.几何分布与指数分布都具备无记忆性

8.泊松分布的应用场景有一天里内商场到店顾客数；单位面积上玻璃上的气泡数等

9.几何分布应用场景有首次抽查到不合格品；首次命中靶心等

10.指数分布被用作各种"寿命"分布，比如通话时长，服务时间，电灯寿命等

11.贝塔分布应用场景有不合格品率、机器的维修率、市场的占有率等

12.二项分布主要应用在一个事件是否为真上，比如风控上好人坏人的概率

概率论中，随机变量分为离散变量和连续变量，对应的分布称为离散分布和连续分布，本文我们介绍常用的两类分布以及用编程如何实现，常见的离散分布有：二项分布、泊松分布、超几何分布和几何分布四种；常见的连续分布有正态分布、均匀分布、指数分布、伽玛分布和贝塔分布五种。除此之外，我们也介绍三大抽样分布：卡方分布、F分布和t分布

1.二项分布

记X为n重伯努利试验中成功（记为事件A）的次数，则X的可能取值为0，1.…，n.记p为每次试验中A发生的概率，即P（A）=p，则这个分布称为二项分布，记为X~b(n,p)

特别地，如果n=1，则二项分布退化为0-1分布（伯努利分布），也称二点分布，记为X~b(1,p)

二项分布X~b(n,p)的期望是np,方差为np(1-p)

利用python的模块scipy可以实现二项分布:

from scipy.stats import binom

#第一个参数表示成功次数k，
#第二个参数是伯努利试验次数n，
#第三个参数是每次试验成功概率p

binom.pmf(5,10,0.5) #概率密度
binom.cdf(5,10,0.5) #累计概率

我们画出n=10，p依次取0.2，0.5，0.8的分布图：

n = 10 #试验次数
m = 0
fig = plt.figure(figsize=(20,6))
for p in [0.2,0.5,0.8]:
    m += 1
    X = np.arange(0, n+1, 1)
    p_list = binom.pmf(X,n,p)
    
    fig.add_subplot(1,3,m)
    plt.plot(X, p_list, linestyle='None', marker='o',color='#DAA520')
    plt.vlines(X, 0, p_list,color='#DAA520')
    plt.xlabel('随机变量X:成功次数k')
    plt.ylabel('Probability')
    plt.title('二项分布X~b({},{})'.format(n,p))

• 位于均值p附近概率较大. 

• 随着p的增加，分布的峰逐渐右移.

2.泊松分布

泊松分布的概率分布列是：

记X~P(λ)

其中，参数λ是单位时间或单位面积内随机事件的平均发生次数。一些常见的场景都服从泊松分布：

• 在一天内，来到某商场的顾客数

• 在单位时间内，一电路受到外界电磁波的冲击次数

• 1平方米内，玻璃上的气泡数

• 一铸件上的砂眼数

• 在一定时期内，某种放射性物质放射出来的α-粒子数

泊松分布具备三个性质：

平稳性: 在一段时间T内，事件发生的概率相同

独立性: 事件的发生彼此独立，没有关联或关联很弱

普通性: 将T划分为无限个小的ΔT, 在每个ΔT内，事件发生多次的概率几乎为0

泊松分布X~P(λ)的期望和方差均是λ

利用python的模块scipy可以实现泊松分布：

from scipy.stats import poisson
lam = 5   #泊松分布的参数λ
poisson.pmf(3,lam) #随机变量取值为k时的概率
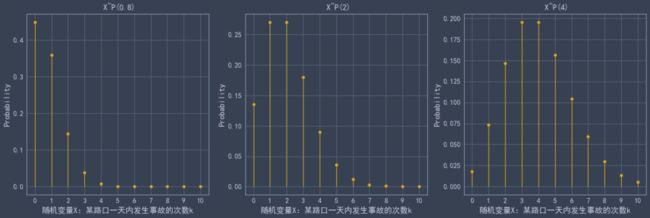
poisson.cdf(7,lam) #累计概率

假设某路口一天发生的事故次数服从泊松分布，我们画出不用参数下的分布图：

m = 0     
fig = plt.figure(figsize=(20,6))
for lam in [0.8,2,4]:
    m += 1
    X = np.arange(0, 11, 1)
    p_list = poisson.pmf(X,lam)
    fig.add_subplot(1,3,m)
    plt.plot(X, p_list, linestyle='None', marker='o',color='#DAA520')
    plt.vlines(X, 0, p_list,color='#DAA520')
    plt.xticks(np.arange(0, 11, 1))
    plt.xlabel('随机变量X：某路口一天内发生事故的次数k')
    plt.ylabel('Probability')
    plt.title(' X~P({})'.format(lam))

• 位于均值λ附近概率较大

• 随着λ的增加，分布逐渐趋于对称

拓展

二项分布的极限就是泊松分布，这是泊松分布一个非常实用的特性。该性质

称为泊松定理：

当n越大，p越小时，两者的近似程度越好

3.超几何分布

从一个有限总体中进行不放回抽样常会遇到超几何分布.

设有N件产品，其中有M件不合格品.若从中不放回地随机抽取n件，则其中含有的不合格品的件数X服从超几何分布，记为X~h(n,N,M).

超几何分布的概率分布列为：

超几何分布X~h(n,N,M)的期望与方差为：

利用python的模块scipy可以实现超几何分布：

from scipy.stats import hypergeom

n = 10 #抽10次
N = 50 #共50件产品
M = 20 #次品的个数
hypergeom.pmf(4,N,M,n) #概率
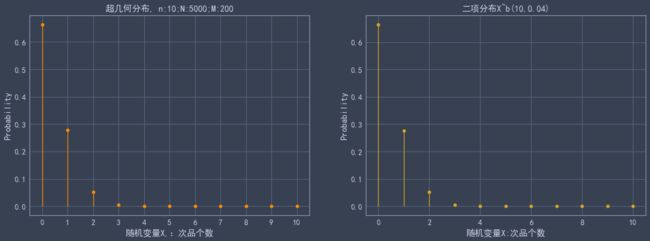
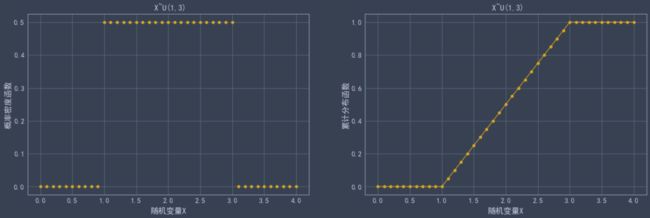
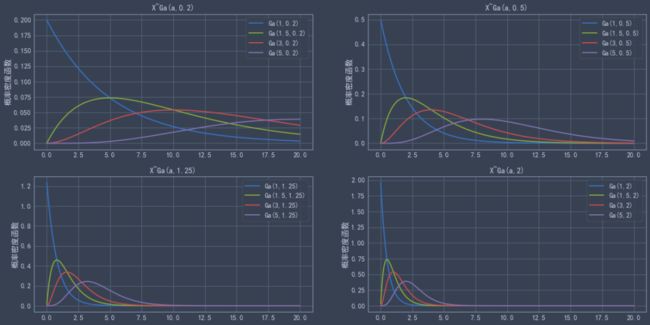
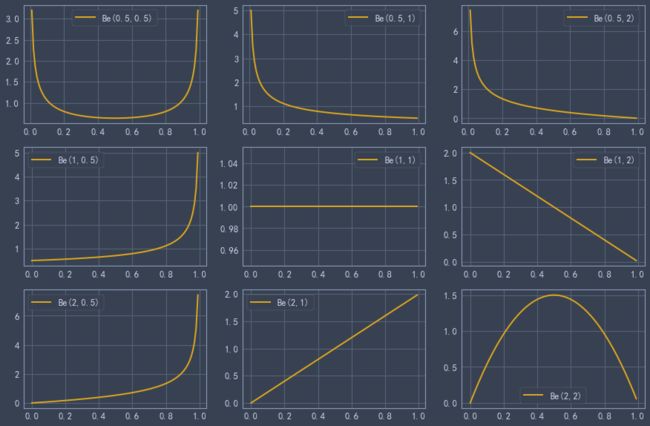
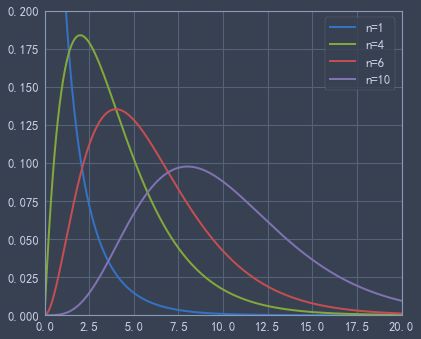
hypergeom.cdf(4,N,M,n) #累计概率

当n<

比如在含有200件次品的5000个样品中抽取10次，超几何分布与二项分布的分布如下：

n = 10 #抽10次
N = 5000 #共50件产品
M = 200 #次品的个数
p = 200/5000 #抓取次品的概率
X = np.arange(0, n+1, 1)
fig = plt.figure(figsize=(18,6))

p_list = hypergeom.pmf(X,N,M,n)
fig.add_subplot(1,2,1)
plt.plot(X, p_list, linestyle='None', marker='o',color='#FF8C00')
plt.vlines(X, 0, p_list,color='#FF8C00')
plt.xticks(np.arange(0, n+1, 1))
plt.xlabel('随机变量X,：次品个数')
plt.ylabel('Probability')
plt.title('超几何分布, n:{};N:{};M:{}'.format(n,N,M))

p_list = binom.pmf(X,n,p)
fig.add_subplot(1,2,2)
plt.plot(X, p_list, linestyle='None', marker='o',color='#DAA520')
plt.vlines(X, 0, p_list,color='#DAA520')
plt.xlabel('随机变量X:次品个数')
plt.ylabel('Probability')
plt.title('二项分布X~b({},{})'.format(n,p))

可见，两者分布近似

4.几何分布

在伯努利试验序列中，记每次试验中事件A发生的概率为p，如果X为事件A首次出现时的试验次数，则X的可能取值为1，2，，…，称X服从几何分布，记为X~Ge(p).

生活很多场景服从几何分布，比如

• 某产品的不合格率为0.05，则首次查到不合格品的检查次数X~Ge(0.05)

• 某射手的命中率为0.8，则首次击中目标的射击次数Y~Ge(0.8)

• 掷一颗骰子，首次出现6点的投掷次数 Z~Ge(1/6)

• 同时掷两颗骰子，首次达到两个点数之和为8的投掷次数W~Ge(5/36)

几何分布X~Ge(p)的期望为1/p,方差是(1-p)/(p^2)

利用python模块scipy可以实现几何分布。

from scipy.stats import geom

p = 0.2
geom.pmf(8,p) #第k次才发生的概率
geom.cdf(8,p) #累计概率

几何分布具有无记忆性：

P(X>m+n|X>m)=P(X>n)

该含义是说：对于几何分布的事件A，前m次试验都没有发生的前提下，在接下去的n次试验中A仍未出现的概率只与n有关，而与前m次试验无关

5.正态分布

正态分布也称高斯分布，是最常见的连续分布。

若随机变量X的密度函数为：

则称X服从正态分布，称X为正态变量，记作X~N(μ，σ^2)

其分布函数为

利用python可以实现正态分布：

from scipy.stats import norm

#第一个参数，随机变量X的取值
#第二个参数，正态分布均值
#第三份参数，正态分布方差
norm.pdf(8,0,1) #概率密度
norm.cdf(8,0,1) #分布函数值

比较不同均值、方差下的正态分布图

from scipy.stats import norm
fig = plt.figure(figsize=(20,6))

x = np.linspace(-10, 40, 1000)
fig.add_subplot(1,2,1)
plt.plot(x, norm.pdf(x,5,7), label='N(5,7)')
plt.plot(x, norm.pdf(x,20,7), label='N(20,7)')
plt.legend()

x = np.linspace(-10, 10, 1000)
fig.add_subplot(1,2,2)
plt.plot(x, norm.pdf(x,0,1), label='N(0,1)')
plt.plot(x, norm.pdf(x,0,2), label='N(0,2)')
plt.plot(x, norm.pdf(x,0,5), label='N(0,5)')
plt.axis([-10,10,0,0.5])
plt.legend()
plt.show()

6.均匀分布

若连续随机变量X的密度函数为

则称X服从区间(a,b)上的均匀分布，记为X~U(a,b)

其分布函数为

均匀分布X~U(a,b)的期望与方差为：

利用python可以实现均匀分布：

from scipy.stats import uniform

#第一个参数，随机变量X取值
#第二个参数，均匀分布参数a
#第三个参数，均匀分布参数b与参数a的差值
uniform.pdf(1.5,1,2) #概率密度函数
uniform.cdf(1.5,1,2) #累计分布函数

生成一个U(1,3)的均匀分布，其概率密度函数和累计分布函数为：

X = np.linspace(0,4,41)
a = 1
e = 2

fig = plt.figure(figsize=(20,6))

p_list = uniform.pdf(X,1,2)
fig.add_subplot(1,2,1)
plt.plot(X, p_list, linestyle='None', marker='o',color='#DAA520')
plt.xlabel('随机变量X')
plt.ylabel('概率密度函数')
plt.title(' X~U({},{})'.format(a,a+e))

p_list = uniform.cdf(X,1,2)
fig.add_subplot(1,2,2)
plt.plot(X, p_list, linestyle='-', marker='o',color='#DAA520')
plt.xlabel('随机变量X')
plt.ylabel('累计分布函数')
plt.title(' X~U({},{})'.format(a,a+e))

7.指数分布

若随机变量X的密度概率函数为

则称X服从指数分布，记为X~Exp(λ),参数λ表示同一事件发生的平均时间间隔

其累计分布函数为

指数分布是一种偏态分布，由于指数分布分布密度函数随机变量只可能取非负实数，所以指数分布常被用作各种"寿命"分布，譬如电子元器件的寿命、动物的寿命、电话的通话时间、随机服务系统中的服务时间等都可假定服从指数分布.指数分布在可靠性与排队论中有着广泛的应用.

指数分布X~Exp(λ)的期望为1/λ，方差为1/(λ^2)

利用python可以实现指数分布

from scipy.stats import expon
#第一个参数，随机变量X取值
#第二个参数，指数分布参数λ的倒数
expon.pdf(1,scale=3) #概率密度函数
expon.cdf(1,scale=3) #累计分布函数

不同参数下指数分布如下：

from scipy.stats import expon

lam1 = 0.5 
lam2 = 1
lam3 = 3
X = np.arange(0,5, 0.01)
p_list1 = expon.pdf(X,scale=1/lam1) # 内置函数是使用1/lam作为参数，即间隔(每天来的人之间的间隔时间)。
p_list2 = expon.pdf(X,scale=1/lam2)
p_list3 = expon.pdf(X,scale=1/lam3)

plt.plot(X, p_list1, linestyle='-',lw=2, marker='None',label='Exp({})'.format(lam1))
plt.plot(X, p_list2, linestyle='-',lw=2, marker='None',label='Exp({})'.format(lam2))
plt.plot(X, p_list3, linestyle='-',lw=2,marker='None',label='Exp({})'.format(lam3))
plt.xlabel('随机变量X：事件发生的时间间隔时长')
plt.ylabel('Probability')
plt.legend()
plt.title('指数分布')

指数分布也具有无记忆性：如果随机变量X服从指数分布，则对任意s>0,t>0，有

P(X>s+t|X>s)=P(X>t)

8.伽玛分布

先介绍伽玛函数：

伽玛函数具有以下性质：

若随机变量X的密度函数为

则称变量X服从伽玛分布，记为X~Ga(α，λ），其中α为形状参数，λ为尺度参数。

伽玛分布X~Ga(α，λ）的期望为α/λ，方差为α/(λ^2)

利用python可以实现伽玛分布

from scipy.stats import gamma
#第一个参数，随机变量X的取值
#第二个参数，形状参数α
#第三个参数，尺度参数λ的倒数
a = 2
lam = 3
gamma.pdf(1,a,scale=1/lam) #概率密度函数
gamma.cdf(1,a,scale=1/lam) #累计概率分布

比较不同形状参数α与尺度参数λ下的伽玛分布

lam = [0.2,0.5,1.25,2]
fig = plt.figure(figsize=(20,10))
m = 0 
for l in lam:
    m += 1
    x = np.arange(0.01,20,0.01)
    p_list1 = gamma.pdf(x,1,scale=1/l)
    p_list2 = gamma.pdf(x,2,scale=1/l)
    p_list3 = gamma.pdf(x,3,scale=1/l)
    p_list4 = gamma.pdf(x,5,scale=1/l)
    
    fig.add_subplot(2,2,m)
    plt.plot(x, p_list1, linestyle='-', lw=2, marker='None',label='Ga({},{})'.format(1,l))
    plt.plot(x, p_list2, linestyle='-', lw=2,marker='None',label='Ga({},{})'.format(1.5,l))
    plt.plot(x, p_list3, linestyle='-', lw=2,marker='None',label='Ga({},{})'.format(3,l))
    plt.plot(x, p_list4, linestyle='-', lw=2,marker='None',label='Ga({},{})'.format(5,l))
    plt.ylabel('概率密度函数')
    plt.legend()
    plt.title('X~Ga(a,{})'.format(l))

可以看到：

• 当0<α<1时，p(x)是严格下降函数，且在x=0处有奇异点

• 当α=1时，p(x)是严格下降函数，且在x=0处p(0)=λ

• 当1<α≤2时，p(x)是单峰函数，先上凸、后下凸

• 当α>2时，p(x)是单峰函数，先下凸、中间上凸、后下凸;且α越大，p(x)越近似于正态密度，但伽玛分布总是偏态分布，α愈小其偏斜程度愈严重

9.贝塔分布

先介绍贝塔函数

贝塔函数具备以下性质：

若随机变量X的密度函数为

则称X服从贝塔分布，记为X~Be(a,b)。其中a,b是形状参数.

在不合格品率、机器的维修率、市场的占有率、射击的命中率等各种比率选用贝塔分布作为它们的概率分布是恰当的，只要选择合适的参数a与b即可.

贝塔分布X~Be(a,b)的期望与方差为：

利用python可实现贝塔分布

from scipy.stats import beta
#第一个参数，随机变量X取值
#第二个参数，beta分布参数a
#第二个参数,beta分布参数b
beta.pdf(0.5,1,2) #概率密度函数
beta.cdf(0.5,1,2) #累计分布函数

不同参数下贝塔分布

from scipy.stats import beta

a = [0.5,1,2]
b = [0.5,1,2]
fig = plt.figure(figsize=(15,10))
m = 0 
for i in a:
    for j in b:
        m += 1
        x = np.arange(0,1,0.01)
        p_list = beta.pdf(x,i,j)
        fig.add_subplot(3,3,m)
        plt.plot(x, p_list, linestyle='-', lw=2, color='#DAA520',marker='None',label='Be({},{})'.format(i,j))
        plt.legend()

可见，

当a<1，b<1时，p(x)是下凸的U形函数

当a>1，b>1时，p(x)是上凸的单峰函数

当a<1，b≥1时，p(x)是下凸的单调减函数

当a≥1，b<1时，p(x)是下凸的单调增函数

当a=1，b=1时，p(x)是常数函数，且Be(1，1)=U(0，1)

10.卡方分布

卡方分布的概率密度函数为

卡方分布期望是自由度n，方差为2n

利用python可以实现卡方分布

from scipy.stats import chi2
#第一个参数，卡方密度函数变量y
#第二哥参数，卡方自由度n
chi2.pdf(5,2) #概率密度函数
chi2.cdf(5,2) #累计分布函数

观测不同自由度下卡方的分布曲线

from scipy.stats import chi2

x = np.linspace( 0, 20, 1000)
plt.plot(x, chi2.pdf(x,1), lw=2, label='n=1')
plt.plot(x, chi2.pdf(x,4), lw=2, label='n=4')
plt.plot(x, chi2.pdf(x,6), lw=2, label='n=6')
plt.plot(x, chi2.pdf(x,10),lw=2, label='n=10')
plt.axis([0,20,0,0.2])
plt.legend()
plt.show()

11.F分布

F分布的概率密度函数为

F分布F~F(m,n)的期望与方差为

利用python可以实现F分布

from scipy.stats import f
#第一个参数，F分布随机变量y取值
#第二个参数，F分布分子自由度m
#第三个参数，F分布分母自由度n
f.pdf(2,4,1)#概率密度函数
f.cdf(2,4,1)#累计分布函数

不同自由度下F的分布曲线

from scipy.stats import f

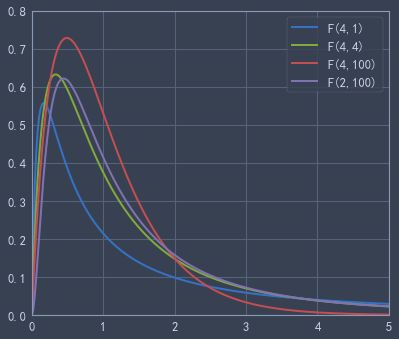
x = np.linspace( 0, 20, 1000)
plt.plot(x, f.pdf(x,4,1), lw=2,label='F(4,1)')
plt.plot(x, f.pdf(x,4,4), lw=2,label='F(4,4)')
plt.plot(x, f.pdf(x,4,100), lw=2,label='F(4,100)')
plt.plot(x, f.pdf(x,6,4), lw=2,label='F(2,100)')
plt.axis([0,5,0,0.8])
plt.legend()
plt.show()

12.t分布

t分布的概率密度函数为

t分布t~t(n)的数学期望与方差为

• E(t)=0，n>1

• Var(t)=n/(n-2)，n>2

利用python可实现t分布

from scipy.stats import t
#第一个参数，t分布随机变量y取值
#第二个参数，t分布自由度n

t.pdf(2,1)#概率密度函数
t.cdf(2,1)#累计分布函数

不同自由度下t分布曲线

from scipy.stats import t

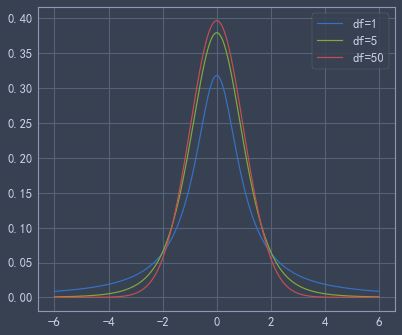
x = np.linspace( -6, 6, 1000)
plt.plot(x, t.pdf(x,1), label='df=1')
plt.plot(x, t.pdf(x,5), label='df=5')
plt.plot(x, t.pdf(x,50), label='df=50')
plt.legend()
plt.show()

参考资料：

《概率论与数理统计（第二版）》

https://blog.csdn.net/u011702002/article/details/78245804