全景图

在同一位置（即图像的照相机位置相同）拍摄的两幅或者多幅图像是单应性相关的。我们经常使用该约束将很多图像缝补起来，拼成一个大的图像来创建全景图像。

RANSAC

RANSAC 是“RANdom SAmple Consensus”（随机一致性采样）的缩写。该方法是用来找到正确模型来拟合带有噪声数据的迭代方法。给定一个模型，例如点集之间的单应性矩阵，RANSAC 基本的思想是，数据中包含正确的点和噪声点，合理的模型应该能够在描述正确数据点的同时摒弃噪声点。

RANSAC 的标准例子：用一条直线拟合带有噪声数据的点集。简单的最小二乘在该例子中可能会失效，但是 RANSAC 能够挑选出正确的点，然后获取能够正确拟合的直线。下面来看使用 RANSAC 的例子。你可以从 http://www.scipy.org/Cookbook/RANSAC 下载 ransac.py，里面包含了特定的例子作为测试用例。

稳健的单应性矩阵估计

使用RANSAC算法求解单应性矩阵 RansacModel类是用于测试单应性矩阵的类 里面包含了fit（）和get_error()方法

fit()方法计算选取的四个对应的单应性矩阵

get_error() 是对所有的对应计算单应性矩阵，然后对每个变换后的点，返回相应的误差

class RansacModel(object):
    """ Class for testing homography fit with ransac.py from
        http://www.scipy.org/Cookbook/RANSAC"""
 
    def __init__(self, debug=False):
        self.debug = debug
 
    def fit(self, data):
        """ Fit homography to four selected correspondences. """
 
        # transpose to fit H_from_points()
        data = data.T
 
        # from points
        fp = data[:3, :4]
        # target points
        tp = data[3:, :4]
 
        # fit homography and return
        return H_from_points(fp, tp)
 
    def get_error(self, data, H):
        """ Apply homography to all correspondences,
            return error for each transformed point. """
 
        data = data.T
 
        # from points
        fp = data[:3]
        # target points
        tp = data[3:]
 
        # transform fp
        fp_transformed = dot(H, fp)
 
        # normalize hom. coordinates
        for i in range(3):
            fp_transformed[i]/=fp_transformed[2]
 
        # return error per point
        return sqrt(sum((tp - fp_transformed) ** 2, axis=0))

H_from_ransac() 使用RANSAC稳健性估计点对应间的单应性矩阵H。该函数允许提供阈值和最小期望的点对数目。最重要的参数是最大迭代次数：程序退出太早可能得到一个坏解；迭代次数太多会占有太多时间。函数的返回结果为单应性矩阵和对应该单应性矩阵的正确点对。

def H_from_ransac(fp, tp, model, maxiter=1000, match_theshold=10):
    """ Robust estimation of homography H from point
        correspondences using RANSAC (ransac.py from
        http://www.scipy.org/Cookbook/RANSAC).
        input: fp,tp (3*n arrays) points in hom. coordinates. """
 
    import ransac
 
    # group corresponding points
    data = vstack((fp, tp))
 
    # compute H and return
    H, ransac_data = ransac.ransac(data.T, model, 4, maxiter, match_theshold, 10, return_all=True)
    return H, ransac_data['inliers']

代码实现

from pylab import *
from numpy import *
from PIL import Image

# If you have PCV installed, these imports should work
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift

# 设置数据文件夹的路径
featname = ['image/' + str(i + 1) + '.sift' for i in range(5)]
imname = ['image/' + str(i + 1) + '.jpg' for i in range(5)]

# 使用sift特征自动找到匹配对应
l = {}
d = {}
for i in range(5):
    sift.process_image(imname[i], featname[i])
    l[i], d[i] = sift.read_features_from_file(featname[i])

matches = {}
for i in range(4):
    matches[i] = sift.match(d[i + 1], d[i])

# 可视化两张图像
for i in range(4):
    im1 = array(Image.open(imname[i]))
    im2 = array(Image.open(imname[i + 1]))
    figure()
    sift.plot_matches(im2, im1, l[i + 1], l[i], matches[i], show_below=True)


# 将匹配项转化为特征点
def convert_points(j):
    ndx = matches[j].nonzero()[0]
    fp = homography.make_homog(l[j + 1][ndx, :2].T)
    ndx2 = [int(matches[j][i]) for i in ndx]
    tp = homography.make_homog(l[j][ndx2, :2].T)

    # switch x and y - TODO this should move elsewhere
    fp = vstack([fp[1], fp[0], fp[2]])
    tp = vstack([tp[1], tp[0], tp[2]])
    return fp, tp


# 估计单应性矩阵
model = homography.RansacModel()

fp, tp = convert_points(1)
H_12 = homography.H_from_ransac(fp, tp, model)[0]  # im 1 to 2

fp, tp = convert_points(0)
H_01 = homography.H_from_ransac(fp, tp, model)[0]  # im 0 to 1

tp, fp = convert_points(2)  # NB: reverse order
H_32 = homography.H_from_ransac(fp, tp, model)[0]  # im 3 to 2

tp, fp = convert_points(3)  # NB: reverse order
H_43 = homography.H_from_ransac(fp, tp, model)[0]  # im 4 to 3

# 扭曲图像
delta = 2000  # for padding and translation

im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12, im1, im2, delta, delta)

im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12, H_01), im1, im_12, delta, delta)

im1 = array(Image.open(imname[3]), "f")
im_32 = warp.panorama(H_32, im1, im_02, delta, delta)

im1 = array(Image.open(imname[4]), "f")
im_42 = warp.panorama(dot(H_32, H_43), im1, im_32, delta, 2 * delta)

figure()
imshow(array(im_42, "uint8"))
axis('off')
show()

结果分析

原图：

sift特征匹配：




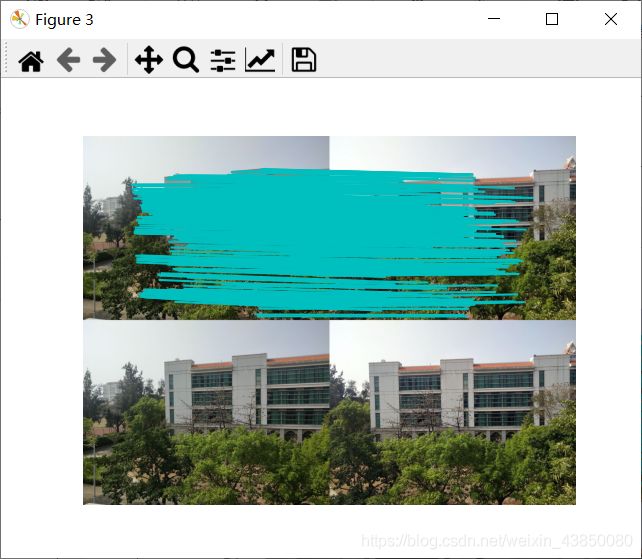
拼接结果：

这是针对于远景图片拼接的结果图，因为将五张图片的像素调为1000*750，所以会比较模糊，但是可以大致的看出拼接的结果是不错的，比较好的还原了拍摄的全景图，不过算法并未考虑全局拼接多张图片平均亮度的问题，出现了分割很明显的部分。

实验总结

1. 图像大小会影响程序的速度，所以要对图片进行压缩，图片太大的话会出现错误
   
2. 图片全景拼接把几张图片拼接在一起，先选取一个中间图像作为中心图像，也就是希望将其他图像变成的图像，由于匹配是从最右边的图像开始计算，所以需要注意将图片的顺序进行颠倒（即由1，2，3，4，5的存放顺序变为5，4，3，2，1），使得从左边图像开始扭曲，将所有图像扭曲到一个公共的图像平面上。