姓名:谢意远
学号:19021110366T
嵌牛导读:图像中的目标物体是连接在一起的,则分割起来很困难,分水岭分割算法经常用于处理这类问题,通常会取得比较好的效果。
嵌牛鼻子:图像分割、分水岭算法
嵌牛提问:分水岭算法具体有哪些步骤?
嵌牛正文:
一、综述
分水岭分割算法把图像看成一幅“地形图”,其中亮度比较强的区域像素值较大,而比较暗的区域像素值较小,通过寻找“汇水盆地”和“分水岭界限”,对图像进行分割。而直接应用分水岭分割算法的效果往往并不好,如果在图像中对前景对象和背景对象进行标注区别,再应用分水岭算法会取得较好的分割效果。基于标记控制的分水岭分割方法有以下基本步骤:
1 综述
分水岭分割算法把图像看成一幅“地形图”,其中亮度比较强的区域像素值较大,而比较暗的区域像素值较小,通过寻找“汇水盆地”和“分水岭界限”,对图像进行分割。直接应用分水岭分割算法的效果往往并不好,如果在图像中对前景对象和背景对象进行标注区别,再应用分水岭算法会取得较好的分割效果。基于标记控制的分水岭分割方法有以下基本步骤:
1.计算分割函数。图像中较暗的区域是要分割的对象
2.计算前景标志。这些是每个对象内部连接的斑点像素。
3.计算背景标志。这些是不属于任何对象的要素。
4.修改分割函数,使其仅在前景和后景标记位置有极小值。
5.对修改后的分割函数做分水岭变换计算。
使用MATLAB图像处理工具箱
注:期间用到了很多图像处理工具箱的函数,例如fspecial、imfilter、watershed、label2rgb、imopen、imclose、imreconstruct、imcomplement、imregionalmax、bwareaopen、graythresh和imimposemin函数等。
2 步骤
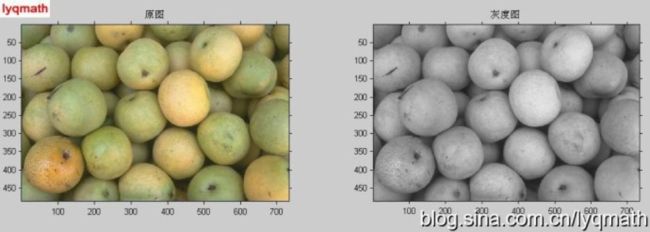
第一步:读入彩色图像,将其转化成灰度图像
clc; clear all; close all;
rgb = imread('pears.png');
if ndims(rgb) == 3
I = rgb2gray(rgb);
else
I = rgb;
end
figure('units', 'normalized', 'position', [0 0 1 1]);
第2步:将梯度幅值作为分割函数
使用Sobel边缘算子对图像进行水平和垂直方向的滤波,然后求取模值,sobel算子滤波后的图像在边界处会显示比较大的值,在没有边界处的值会很小。
hy = fspecial('sobel');
hx = hy';
Iy = imfilter(double(I), hy, 'replicate');
Ix = imfilter(double(I), hx, 'replicate');
gradmag = sqrt(Ix.^2 + Iy.^2);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(I,[]), title('灰度图像')
subplot(1, 2, 2); imshow(gradmag,[]), title('梯度幅值图像')
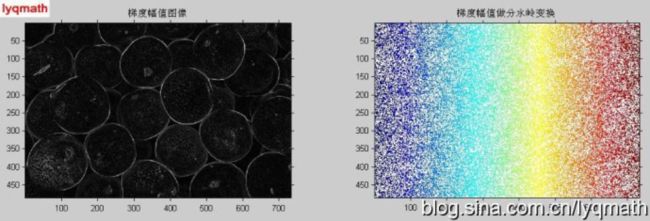
可否直接对梯度幅值图像使用分水岭算法?
L = watershed(gradmag);
Lrgb = label2rgb(L);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(gradmag,[]), title('梯度幅值图像')
subplot(1, 2, 2); imshow(Lrgb); title('梯度幅值做分水岭变换')
直接使用梯度模值图像进行分水岭算法得到的结果往往会存在过度分割的现象。因此通常需要分别对前景对象和背景对象进行标记,以获得更好的分割效果。
第3步:标记前景对象
有多种方法可以应用在这里来获得前景标记,这些标记必须是前景对象内部的连接斑点像素。这个例子中,将使用形态学技术“基于开的重建”和“基于闭的重建”来清理图像。这些操作将会在每个对象内部创建单位极大值,使得可以使用imregionalmax来定位。
开运算和闭运算:先腐蚀后膨胀称为开;先膨胀后腐蚀称为闭。开和闭这两种运算可以除去比结构元素小的特定图像细节,同时保证不产生全局几何失真。开运算可以把比结构元素小的突刺滤掉,切断细长搭接而起到分离作用;闭运算可以把比结构元素小的缺口或孔填充上,搭接短的间隔而起到连接作用。
开操作是腐蚀后膨胀,基于开的重建(基于重建的开操作)是腐蚀后进行形态学重建。下面比较这两种方式。首先,用imopen做开操作。
se = strel('disk', 20);
Io = imopen(I, se);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(I, []); title('灰度图像');
subplot(1, 2, 2); imshow(Io), title('图像开操作')
接下来,通过腐蚀后重建来做基于开的重建计算。
Ie = imerode(I,se)
Iobr = imreconstruct(Ie,I);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(I, []); title('灰度图像');
subplot(1, 2, 2); imshow(Iobr, []), title('基于开的重建图像')
开操作后,接着进行闭操作,可以移除较暗的斑点和枝干标记。对比常规的形态学闭操作和基于闭的重建操作。首先,使用imclose:
Ioc = imclose(Io, se);
Ic = inclose(I,se);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(I, []); title('灰度图像');
subplot(2, 2, 2); imshow(Io, []); title('开操作图像');
subplot(2, 2, 3); imshow(Ic, []); title('闭操作图像');
subplot(2, 2, 4); imshow(Ioc, []), title('开闭操作');
现在使用imdilate,然后使用imreconstruct。注意必须对输入图像求补,对imreconstruct输出图像求补。IM2 = imcomplement(IM)计算图像IM的补集。IM可以是二值图像,或者RGB图像。IM2与IM有着相同的数据类型和大小。
Iobrd = imdilate(Iobr, se);
Iobrcbr = imreconstruct(imcomplement(Iobrd), imcomplement(Iobr));
Iobrcbr = imcomplement(Iobrcbr);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(I, []); title('灰度图像');
subplot(2, 2, 2); imshow(Ioc, []); title('开闭操作');
subplot(2, 2, 3); imshow(Iobr, []); title('基于开的重建图像');
subplot(2, 2, 4); imshow(Iobrcbr, []), title('基于闭的重建图像');
通过比较Iobrcbr和loc可以看到,在移除小污点同时不影响对象全局形状的应用下,基于重建的开闭操作要比标准的开闭重建更加有效。计算Iobrcbr的局部极大来得到更好的前景标记。
fgm = imregionalmax(Iobrcbr);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 3, 1); imshow(I, []); title('灰度图像');
subplot(1, 3, 2); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(1, 3, 3); imshow(fgm, []); title('局部极大图像');
为了帮助理解这个结果,叠加前景标记到原图上。
It1 = rgb(:, :, 1);
It2 = rgb(:, :, 2);
It3 = rgb(:, :, 3);
It1(fgm) = 255; It2(fgm) = 0; It3(fgm) = 0;
I2 = cat(3, It1, It2, It3);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(rgb, []); title('原图像');
subplot(2, 2, 2); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(2, 2, 3); imshow(fgm, []); title('局部极大图像');
subplot(2, 2, 4); imshow(I2); title('局部极大叠加到原图像');
注意到大多闭塞处和阴影对象没有被标记,这就意味着这些对象在结果中将不会得到合理的分割。而且,一些对象的前景标记会一直到对象的边缘。这就意味着应该清理标记斑点的边缘,然后收缩它们。可以通过闭操作和腐蚀操作来完成。
se2 = strel(ones(5,5));
fgm2 = imclose(fgm, se2);
fgm3 = imerode(fgm2, se2);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(2, 2, 2); imshow(fgm, []); title('局部极大图像');
subplot(2, 2, 3); imshow(fgm2, []); title('闭操作');
subplot(2, 2, 4); imshow(fgm3, []); title('腐蚀操作');
这个过程将会留下一些偏离的孤立像素,应该移除它们。可以使用bwareaopen,用来移除少于特定像素个数的斑点。BW2 = bwareaopen(BW,P)从二值图像中移除所以少于P像素值的连通块,得到另外的二值图像BW2。
fgm4 = bwareaopen(fgm3, 20);
It1 = rgb(:, :, 1);
It2 = rgb(:, :, 2);
It3 = rgb(:, :, 3);
It1(fgm4) = 255; It2(fgm4) = 0; It3(fgm4) = 0;
I3 = cat(3, It1, It2, It3);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(I2, []); title('局部极大叠加到原图像');
subplot(2, 2, 2); imshow(fgm3, []); title('闭腐蚀操作');
subplot(2, 2, 3); imshow(fgm4, []); title('去除小斑点操作');
subplot(2, 2, 4); imshow(I3, []); title('修改局部极大叠加到原图像');
第4步:计算背景标记
现在,需要标记背景。在清理后的图像Iobrcbr中,暗像素属于背景,所以可以从阈值操作开始。
bw =im2bw(Iobrcbr, graythresh(Iobrcbr));
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(1, 2, 2); imshow(bw, []); title('阈值分割');
背景像素在黑色区域,但是理想情形下,不必要求背景标记太接近于要分割的对象边缘。通过计算“骨架影响范围”来“细化”背景,或者SKIZ,bw的前景。这个可以通过计算bw的距离变换的分水岭变换来实现,然后寻找结果的分水岭脊线(DL==0)。D = bwdist(BW)计算二值图像BW的欧几里得矩阵。对BW的每一个像素,距离变换指定像素和最近的BW非零像素的距离。bwdist默认使用欧几里得距离公式。BW可以由任意维数,D与BW有同样的大小。
D = bwdist(bw);
DL = watershed(D);
bgm = DL == 0;
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2, 2, 1); imshow(Iobrcbr, []); title('基于重建的开闭操作');
subplot(2, 2, 2); imshow(bw, []); title('阈值分割');
subplot(2, 2, 3); imshow(label2rgb(DL), []); title('分水岭变换示意图');
subplot(2, 2, 4); imshow(bgm, []); title('分水岭变换脊线图');
第5步:计算分割函数的分水岭变换
函数imimposemin可以用来修改图像,使其只是在特定的要求位置有局部极小。这里可以使用imimposemin来修改梯度幅值图像,使其只在前景和后景标记像素有局部极小。
gradmag2 = imimposemin(gradmag, bgm | fgm4);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(2,2,1)imshow(bgm,[]);title('分水岭变换脊线图');
subplot(2, 2, 2); imshow(fgm4, []); title('前景标记');
subplot(2, 2, 3); imshow(gradmag, []); title('梯度幅值图像');
subplot(2, 2, 4); imshow(gradmag2, []); title('修改梯度幅值图像');
最后,可以做基于分水岭的图像分割计算。
第6步:查看结果
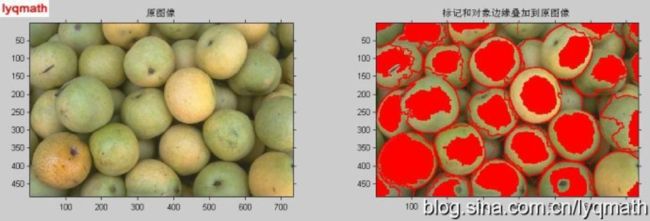
一个可视化技术是叠加前景标记、背景标记、分割对象边界到初始图像。可以使用膨胀来实现某些要求,比如对象边界,更加清晰可见。对象边界定位于L==0的位置。
It1 = rgb(:, :, 1);
It2 = rgb(:, :, 2);
It3 = rgb(:, :, 3);
fgm5 = imdilate(L == 0, ones(3, 3)) | bgm | fgm4;
It1(fgm5) = 255; It2(fgm5) = 0; It3(fgm5) = 0;
I4 = cat(3, It1, It2, It3);
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(rgb, []); title('原图像');
subplot(1, 2, 2); imshow(I4, []); title('标记和对象边缘叠加到原图像');
可视化说明了前景和后景标记如何影响结果。在几个位置,部分的较暗对象与它们相邻的较亮的邻接对象相融合,这是因为受遮挡的对象没有前景标记。
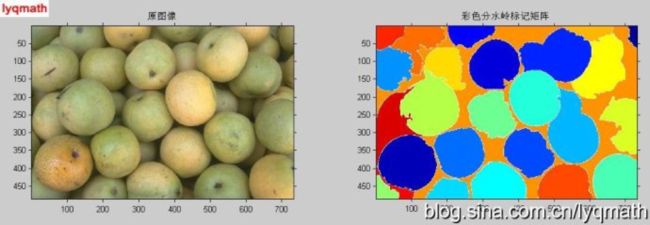
另外一个有用的可视化技术是将标记矩阵作为彩色图像进行显示。标记矩阵,比如通过watershed和bwlabel得到的,可以使用label2rgb转换到真彩图像来显示。
Lrgb = label2rgb(L,'jet', 'w', 'shuffle');
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(rgb, []); title('原图像');
subplot(1, 2, 2); imshow(Lrgb); title('彩色分水岭标记矩阵');
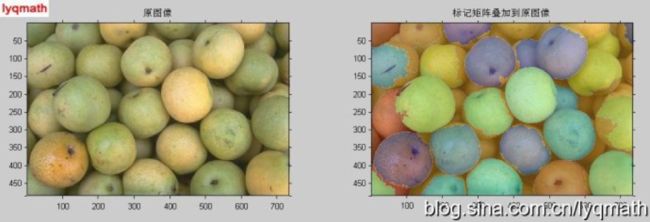
可以使用透明度来叠加这个伪彩色标记矩阵在原亮度图像上进行显示。
figure('units', 'normalized', 'position', [0 0 1 1]);
subplot(1, 2, 1); imshow(rgb, []); title('原图像');
subplot(1, 2, 2); imshow(rgb, []); hold on;
himage = imshow(Lrgb);
set(himage, 'AlphaData', 0.3);
title('标记矩阵叠加到原图像');