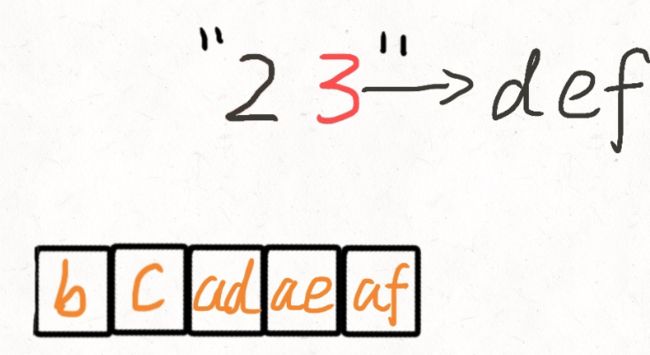1.题目描述
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]
2.思路分析
(1)利用队列求解(BFS)
我们可以利用队列的先进先出特点,再配合循环完成题目要求。
我们先将2对应的字符"a","b","c"依次放入队列中
之后再从队列中拿出第一个元素"a",跟3对应的字符"d","e","f"挨个拼接
于是队列就变成了这个样子:
按照同样的方式,再将"b"从队列中拿出,再跟3对应的字符"d","e","f"挨个拼接.
代码实现:
public static List letterCombinations(String digits) {
//边界条件判断
List list = new ArrayList<>();
if (digits.equals("") || digits == null) {
return list;
}
//先存入一个空字符,从而开始遍历
list.add("");
//1.第一个循环目的是:一共要放入的字符次数
for (int i = 0; i < digits.length(); i++) {
//获取当前字符对应的字符数组
char letters[] = getValue(digits.charAt(i));
//当前字符对应的长度
int size = list.size();
//取出当前list中的所有元素
for (int j = 0; j < size; j++) {
String tmp = list.remove(0);
//然后跟“def”这样的字符串拼接起来
for (int k = 0; k < letters.length; k++) {
list.add(tmp + letters[k]);
}
}
}
return list;
}
private static char[] getValue(char num) {
if (num == '2') {
char nums[] = {'a', 'b', 'c'};
return nums;
} else if (num == '3') {
char nums[] = {'d', 'e', 'f'};
return nums;
} else if (num == '4') {
char nums[] = {'g', 'h', 'i'};
return nums;
} else if (num == '5') {
char nums[] = {'j', 'k', 'l'};
return nums;
} else if (num == '6') {
char nums[] = {'m', 'n', 'o'};
return nums;
} else if (num == '7') {
char nums[] = {'p', 'q', 'r', 's'};
return nums;
} else if (num == '8') {
char nums[] = {'t', 'u', 'v'};
return nums;
} else if (num == '9') {
char nums[] = {'w', 'x', 'y', 'z'};
return nums;
}
return null;
}
(2)回溯法(DFS)
回溯的思想就是:循环中递归调用
一步一步拆解来看:
①如果只有一个字符,例如输入的是“2”,所以结果应该是:["a","b","c"],对应伪代码如下:
result = List()
for(i=0;i②如果有两个字符,输入的是23,应该怎么做呢?23的结果是["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"],对应的伪代码如下:
result = List()
for(i=0;i③如果有三个字符,输入的是234,对应的伪代码:
result = List()
for(i=0;i总结:所以我们发现,循环的嵌套层数跟我们输入的字符长度相关,可如果输入的字符长度不确定,那我们应该怎么办呢?
这个时候,递归就派上了用场!
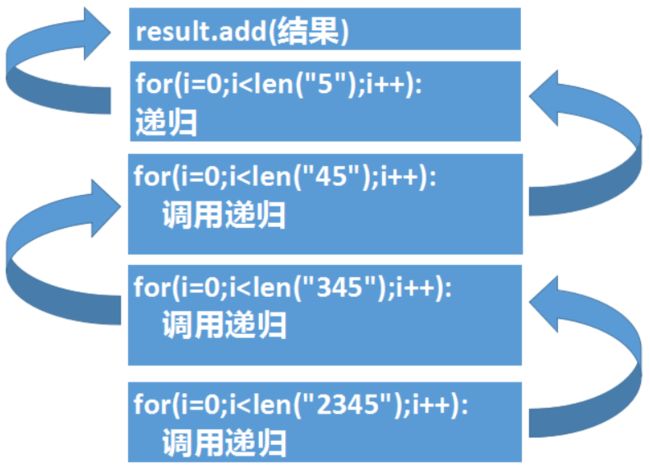
对于打印"2345"这样的字符串:
第一次递归就是上图中最下面的方格,然后处理完第一个字符2之后,将输入的字符改变成"345"并调用第二个递归函数
第二次递归处理3,将字符串改变成"45"后再次递归
第三次递归处理4,将字符串改变成"5"后继续递归
第四次递归处理5,将字符串改变成""后继续递归
最后发现字符串为空了,将结果放到列表中并返回
上面是从函数调用的角度去看的,而每次调用下一层递归时,都需要将本层的一些处理结果放到一个临时变量中,再传递给下一层,从这个变量层层传递的变化看,就像一棵树一样,这个算法的时间复杂度很高,是O(3^n)这个级别的,空间复杂度是O(n)
代码实现:
public static List letterCombinations2(String digits) {
List list = new ArrayList<>();
if (digits.equals("") || digits == null) {
return list;
}
getList(digits, 0, list, "");
return list;
}
public static void getList(String digits, int cur, List list, String curStr) {
if (cur == digits.length()) {
list.add(curStr);
return;
}
char[] arrays = getValue(digits.charAt(cur));
for (int i = 0; i < arrays.length; i++) {
getList(digits, cur + 1, list, curStr + String.valueOf(arrays[i]));
}
}
private static char[] getValue(char num) {
if (num == '2') {
char nums[] = {'a', 'b', 'c'};
return nums;
} else if (num == '3') {
char nums[] = {'d', 'e', 'f'};
return nums;
} else if (num == '4') {
char nums[] = {'g', 'h', 'i'};
return nums;
} else if (num == '5') {
char nums[] = {'j', 'k', 'l'};
return nums;
} else if (num == '6') {
char nums[] = {'m', 'n', 'o'};
return nums;
} else if (num == '7') {
char nums[] = {'p', 'q', 'r', 's'};
return nums;
} else if (num == '8') {
char nums[] = {'t', 'u', 'v'};
return nums;
} else if (num == '9') {
char nums[] = {'w', 'x', 'y', 'z'};
return nums;
}
return null;
}
3.参考文献
https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/solution/tong-su-yi-dong-dong-hua-yan-shi-17-dian-hua-hao-m/