Pytorch 深度学习实践 第3讲
二、梯度下降算法
课程链接:Pytorch 深度学习实践——梯度下降算法
1、梯度下降算法的合理性
①梯度下降算法实际上是一种贪心算法,因此可以找到局部最优点,但是无法保证找到全局最优点。又由于深度学习中的loss函数通常不存在很多的局部最优点,并且还可以通过改变学习率来进行多次实验,因此可以采用梯度下降算法来解决大部分深度学习的问题。
②如果遇到鞍点:gradient=0,那么迭代无法继续,这是梯度下降算法需要解决的问题。
2、MSE Loss函数的梯度下降
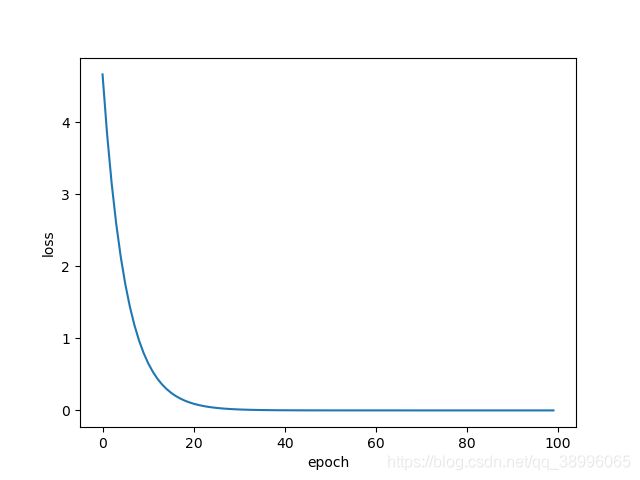
Ⅰ、BGD(Batch Gradient Descent)
梯度更新规则:
BGD 采用整个训练集的数据来计算 cost function 对参数的梯度。
代码实现:
import numpy as np
import matplotlib.pyplot as plt
def forward(x):
return w * x
def loss(y, t):
return np.sum((y-t)**2) / len(y)
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (w * x - y)
return grad / len(xs)
x_data = np.arange(1.0, 4.0, 1.0)
y_data = np.arange(2.0, 8.0, 2.0)
epoch_list = []
loss_list = []
w = 1.0#随机初始化一个值
for epoch in range(100):
y_pred = forward(x_data)
cost = loss(y_pred, y_data)
grad = gradient(x_data, y_data)
w -= 0.01 * grad
loss_list.append(cost)
epoch_list.append(epoch)
if(epoch % 10 == 0):
print('Epoch = ' + str(epoch) + '\t' 'W = ' + str(format(w, '.4f')) + '\t' + 'loss = ' + str(format(cost, '.4f')))
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
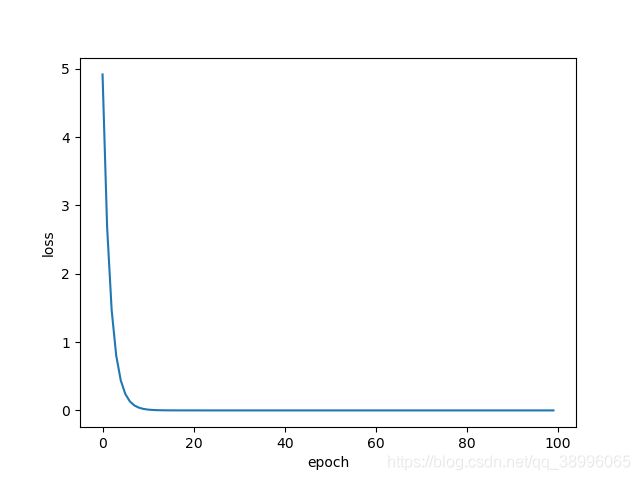
Ⅱ、SGD(Stochastic Gradient Descent):随机梯度下降
梯度更新规则:
和 BGD 的一次用所有数据计算梯度相比,SGD 每次更新时对每个样本进行梯度更新,对于很大的数据集来说,可能会有相似的样本,这样 BGD 在计算梯度时会出现冗余,而 SGD 一次只进行一次更新,就没有冗余,而且比较快,并且可以新增样本。
可以对照BGD看出两者之间的区别:BGD对整个数据集计算梯度,所以计算起来非常慢,针对大样本的数据集可能比较吃力,而且最后的结果可能是局部最优值,性能较差(BGD的缺点),随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况,时间复杂度较高(SGD的缺点),那么可能只用其中部分的样本(Mini-Batch SGD)。
代码实现:
import numpy as np
import matplotlib.pyplot as plt
def forward(x):
return w * x
def loss(y, t):
return (y - t) ** 2
def gradient(x, y):
return 2 * x * (w * x - y)
x_data = np.arange(1.0, 4.0, 1.0)
y_data = np.arange(2.0, 8.0, 2.0)
epoch_list = []
loss_list = []
w = 1.0#随机初始化一个值
for epoch in range(100):
for x, y in zip(x_data, y_data):
grad = gradient(x, y)
w -= 0.01 * grad
t = forward(x)
l = loss(y, t)
if(epoch % 10 == 0):
print('Epoch = ' + str(epoch) + '\t' 'W = ' + str(format(w, '.4f')) + '\t' + 'loss = ' + str(format(l, '.4f')))
loss_list.append(l)
epoch_list.append(epoch)
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
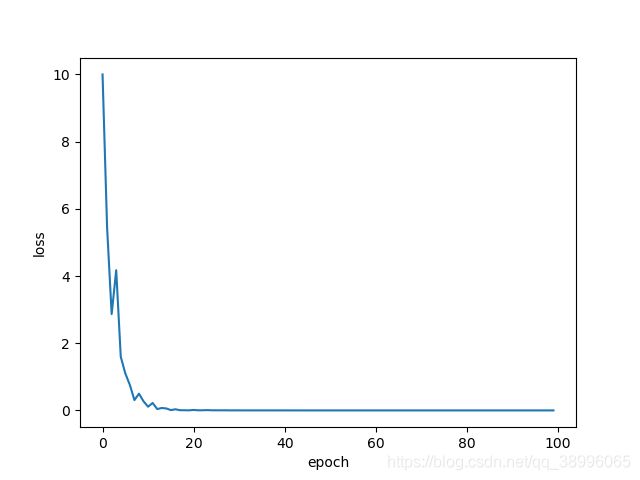
Ⅲ、Mini-Batch SGD
import numpy as np
import matplotlib.pyplot as plt
def forward(x):
return w * x
def loss(y, t):
return np.sum((y-t)**2) / len(y)
def gradient(xs, ys):
grad = 0
for x, y in zip(xs, ys):
grad += 2 * x * (w * x - y)
return grad / len(xs)
x_data = np.arange(1.0, 5.0, 1.0)
y_data = np.arange(2.0, 10.0, 2.0)
train_size = len(x_data)
batch_size = 2
epoch_list = []
loss_list = []
w = 1.0#随机初始化一个值
for epoch in range(100):
#获取mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_data[batch_mask]
y_batch = y_data[batch_mask]
t_batch = forward(x_batch)
cost = loss(y_batch, t_batch)
grad = gradient(x_batch, y_batch)
w -= 0.01 * grad
loss_list.append(cost)
epoch_list.append(epoch)
if(epoch % 10 == 0):
print('Epoch = ' + str(epoch) + '\t' 'W = ' + str(format(w, '.4f')) + '\t' + 'loss = ' + str(format(cost, '.4f')))
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()