图论——最小生成树

最小生成树

什么是最小生成树：

1.生成树：
在一张无向连通有权图中，我们要从一个节点出发，找到一组有权边，将所有节点都连接起来，这样的一组节点和边将构成一颗树，也就是生成树，这颗树是根据图而生成的。
2.最小生成树：
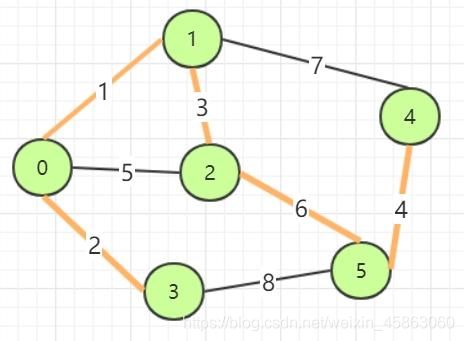
在所有生成树中，如果其中一棵树的所有边的权值和最小，那么就成为最小生成树，不过最小生成树可能不是唯一的。下图中加粗的边就构成了一颗最小生成树。

获得最小生成树的两种算法

1.Kruskal算法
Kruskal算法使用的是一种贪婪策略，首先对于V个节点，我们初始生成包含V棵树的森林，森林中的每一棵树初始本身就是其单个节点。接下来我们将所有边E从小到大排序，并由小到达对其进行遍历，如若找到的一条边（u，v）中u，v不属于同一棵树，那么我们将这个边（u，v）加入到最小生成树的边当中，并将u，v分别所在的两棵树a，b进行合并，合并成同一颗树c，如果u，v所在同一棵树上，那么我们就不对（u，v）进行上述操作，而将其舍弃。重复上述过程，可以不断将森林中的树合并，并不断将遍历到的一些边加入到最小生成树的边当中，当森林中的所有树被合并成一棵树时，这棵树就是最小生成树，算法结束。

用上面的图来描述Kruskal算法的过程：
遍历边的顺序大致如下：
（u,v）  weight   decision
    0,1          1         加入
    0,3          2         加入
    1,2          3         加入
    4,5          4         加入
    0,2          5         舍弃
    2,5          6         加入
    1,4          7         舍弃
    3,5          8         舍弃

下面给出完整的用c实现的Kruskal算法(基于上面给出的图获得最小生成树)：

#include 
#include 
//Kruskal算法获得最小生成树 
# define N 6
//定义邻接表 
int map[N][N]={
     
0,1,5,2,0,0,
1,0,3,0,7,0,
5,3,0,0,0,6,
2,0,0,0,0,8,
0,7,0,0,0,4,
0,0,6,8,4,0
};
//设置邻接表
set_map()
{
     
	int i,j,k;
	for(i=0;i<N;i++)
	{
     
		printf("请输入第%d个节点的邻接关系：\n",i);
		for(j=0;j<N;j++)
		{
     
			printf("通向节点%d的边的权值： ",j) ;
			scanf("%d",&map[i][j]);
		}
	}
	printf("\n邻接表设置完毕\n");
	for(i=0;i<N;i++)
	{
     
		for(j=0;j<N;j++)
		{
     
			printf("%d ",map[i][j]);
		}
		printf("\n");
	}
}
 
//定义边
typedef struct edge
{
     
	int u;
	int v;
	int weight;
 } edge;
 //定义存放边的集合
typedef struct edgeList
{
     
	int size;
	edge edges[N*N];
} edgeList;
//初始化边的集合
Init_edgeList(edgeList ** eL)
{
     
	(*eL)=(edgeList *)malloc(sizeof(edgeList));
	(*eL)->size=0;
	int i,j,k;
	//获得所有边的信息并加入到表中 
	for(i=0;i<N;i++) 
	{
     
		for(j=i+1;j<N;j++)
		{
     
			if(map[i][j]!=0)
			{
     
				(*eL)->edges[(*eL)->size].weight=map[i][j];
				(*eL)->edges[(*eL)->size].u=i;
				(*eL)->edges[(*eL)->size].v=j;
				(*eL)->size++;
			}
		}
	}
	//对所有边按权值从小到大进行排序,即对结构体数组进行排序 
	edge t;
	for(i=1;i<=(*eL)->size;i++)
	{
     
		for(j=0;j<(*eL)->size-i;j++)
		{
     
			if((*eL)->edges[j].weight>(*eL)->edges[j+1].weight)
			{
     
				t=(*eL)->edges[j];
				(*eL)->edges[j]=(*eL)->edges[j+1];
				(*eL)->edges[j+1]=t;
			}
		}
	 } 
 } 
 //定义树
 typedef struct tree
 {
     
 	edge edges[N-1];
 	int vertexs[N];
 	int edge_num;
 	int flag; 
  } tree;
  
//定义森林
typedef struct forest
{
     
	tree trees[N];
	int tree_num;
 } forest;
 //初始化森林和树
 forest* Init_forest()
 {
     
 	int i,j,k;
 	forest *f=(forest*)malloc(sizeof(forest));
 	f->tree_num=N;
 	for(i=0;i<N;i++)
 	{
     
 		for(j=0;j<N;j++) f->trees[i].vertexs[j]=0;
 		f->trees[i].vertexs[i]=1;
 		f->trees[i].edge_num=0;
 		f->trees[i].flag=1;
	 }
	 return f;
  } 
  Union(tree *t1,tree *t2)//合并两棵树 
  {
     
  	int i,j;
  	//将t2中的边加入到t1当中 
  	for(i=0;i<t2->edge_num;i++)
  	{
     
  		t1->edges[t1->edge_num]=t2->edges[i];
  		t1->edge_num++;
	  }
	//将t2中的节点加入到t1当中 
	for(i=0;i<N;i++)
	{
     
		if(t2->vertexs[i]==1)
		{
     
			t1->vertexs[i]=1;
		}
	}
	//将t2标记为舍弃 
	t2->flag=0;
  }
  Kruskal(edgeList *eL,forest *f)
  {
     
  	int i,j,k,n=1;//n表示最小生成树中已经存在的节点数 
  	int u,v,t1=-1,t2=-1;
  	edge e;
  while(n!=N)
  {
     
  	for(i=0;i<N;i++)
  	{
     
  		e=eL->edges[i];
  		u=e.u;
  		v=e.v;
  		//找到u和v分别在哪一棵树当中 
  		for(j=0;j<N;j++)
  		{
     
  			if(f->trees[j].vertexs[u]==1&&f->trees[j].flag)
  			{
     
  				t1=j;
			  }
			if(f->trees[j].vertexs[v]==1&&f->trees[j].flag)
  			{
     
  				t2=j;
			  }	 
		}
		if(t1!=t2)//如果两节点不在同一棵树当中，则将这条边加入最小生成树，并将两棵树进行合并 
		{
     
		  //将这条边加入到树t1中 
		  f->trees[t1].edges[f->trees[t1].edge_num]=e;	
		  f->trees[t1].edge_num++;
		  f->trees[t1].vertexs[v]=1;
		  //将t1和t2进行合并
		  Union(&f->trees[t1],&f->trees[t2]); 
		  f->trees[t2].flag=0;
		  n++;
		 } 
	  }
    }
   } 
int main()
{
     
	//set_map();
	tree MinTree;
	int i,j,k,min_p=0;
	edgeList *eL;
    Init_edgeList(&eL);
    printf("图的邻接关系及边的权重表示如下：\n") ;
    for(i=0;i<eL->size;i++)
    {
     
    	printf("u=%d  v=%d  weight=%d\n",eL->edges[i].u,eL->edges[i].v,eL->edges[i].weight);
	}
	forest * f=Init_forest();
	Kruskal(eL,f);
	//找到最小生成树的所在 
	for(i=0;i<N;i++)
	{
     
		if(f->trees[i].flag!=0)
		{
     
			MinTree=f->trees[i];
		}
	} 
	//打印最小生成树中的每一条边 
	printf("\n最小生成树中的所有边：\n"); 
	for(i=0;i<MinTree.edge_num;i++)
	{
     
		printf("(%d,%d)   weight=%d\n",MinTree.edges[i].u,MinTree.edges[i].v,MinTree.edges[i].weight);
		min_p+=MinTree.edges[i].weight;
	}
	printf("\n最小生成树所有边的权值之和为:%d\n",min_p);
 } 

程序运行后结果显示如下：

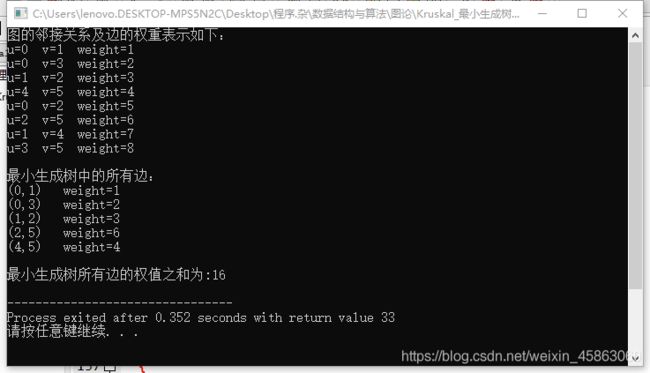
上面这段用c语言实现的Kruskal算法只是我初学Kruskal算法时按照书上给出的算法逻辑写出的，并不是很高效很正统的算法，但我认为是对于初学者来说是好理解并且形象的。