TVM的Tensor数据结构解读

这篇文章主要是解读下TVM中的tvm::te::Tensor以及相关类型的数据结构。

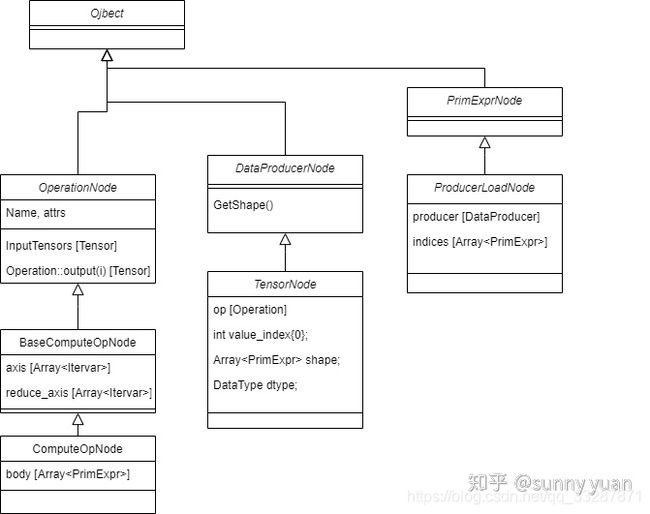
下面给出了TensorNode以及相关数据的类结构示意图。可以看到TensorNode中含有op, value_index, shape, dtype等数据成员。

op的类型是Operation，Operation有InputTensors的成员函数返回Tensor，有output(int i) 成员函数也返回Tensor，可知Operatoin的输入输出都是Tensor类型。

一个Operation可能会有多个输出，TensorNode中的value_index就表示当前tensor是它自身成员变量op的第几个输出。

BaseComputeOpNode中的axis 表达了一个计算当中使用到的循环变量。reduce_axis记录了在哪些维度上进行规约计算。

ComputeOpNode 中的body 记录了具体的计算操作。

以下面的一段代码具体解释下：

import tvm
import tvm.testing
from tvm import te
import numpy as np

n = te.var("n")
A = te.placeholder((n,), name="A")
B = te.placeholder((n,), name="B")
C = te.compute(A.shape, lambda i: A[i] + B[i], name="C")
D = te.compute(A.shape, lambda i: C[i] + B[i], name="D")

上述代码对应的抽象语法树大致如下：

D的类型是Tensor，D.op是ComputeOp类型（继承自Operation）。

D.op.body是Array类型，但是这儿size为1，D.op.body[0]的类型是tvm::tir::Add。Add有两个成员变量，分别是a、b，表达的含义就是a + b。

可以看到上述a 和 b 都是ProducerLoad类型，由图1 的数据结构图可以看到ProducerLoadNode由两个数据成员producer 和 indices。在这个例子当中producer就是Tensor。indices是Array类型，但是这儿的例子当中只是对一维数据进行操作，所以indices的size 为1。

图2中没有对C.op进一步展开，它的展开内容与D.op类似。

再看下面一段代码：

n0 = te.var("n0")
n1 = te.var("n1")
A0 = te.placeholder((n0,n1), name="A")
A1 = te.placeholder((n0,n1), name="B")
B0, B1 = te.compute((n0,n1), lambda i, j: (A0[i, j] + 2, A1[i, j] * 3), name="S")

B0， B1是两个Tensor，打印可知B0.op == B1.op， B0.value_index = 0, B1.value_index=1，说明B0, B1 是同一个Operation的两个输出。

InputTensors 函数

在了解了Tensor相关的数据结构之后，现在来看下ComputeOpNode::InputTensors()函数的实现逻辑。

Array ComputeOpNode::InputTensors() const {
  Array ret;
  std::unordered_set visited;
  for (auto& e : body) {
    tir::PostOrderVisit(e, [&ret, &visited](const ObjectRef& n) {
      if (auto* pload = n.as()) {
        Tensor t = Downcast(pload->producer);
        if (!visited.count(t)) {
          ret.push_back(t);
          visited.insert(t);
        }
      }
    });
  }
  return ret;
}

首先遍历body部分，例如上面的例子当中B0, B1对应的op的body包含两个body，并且两个body有各自的不同输入Tensor。

然后对每个body部分采取后续遍历的方式，其实看到PostOrderVisit，然后再对照之前讲过的语法树结构，应该就能理解下，下面再举个例子巩固下。

n = te.var("n")
A = te.placeholder((n,), name="A")
B = te.placeholder((n,), name="B")
E = te.placeholder((n,), name="E")
C = te.compute(A.shape, lambda i: A[i] + B[i] + E[i], name="C")

如果打印C.op.input_tensors ，那么应该有三个输入A，B，E。

下面画下AST:

对上面的AST进行后续遍历，那么遍历的结果是A[i], B[i], (A[i]+B[i]) , E[i], ((A[i]+B[i])+E[i])。其中A[i], B[i], E[i]这三个节点是ProducerLoadNode类型，会把他们的内部producer元素添加到InputTensors的返回结果中。

注意代码在遍历ProducerLoad节点的时候，是不会继续去遍历它的producer成员变量的。