Game Theory
This week you should
- watch Game Theory.
- The readings are Littman (1994), Littman and Stone (2003), Greenwald and Hall (2003), and Munoz de Cote and Littman (2008).
11B Game Theory ReLoaded
Iterated Prisoner's Delama
- Prisoner should always defects at the last game (say we have k games), then the kth game is known
- If you do the above choice, then the last game is known, and the last unknow game becomes to be the one before.
- since prisoner should defect in the last unknown game, then it should defect on the (k - 1) th game. And the (k - 1)th game becomes known.
- So prisoners should always defect at every each game
- but what happens when the last a few games are unknown?
Uncertain End
- the probability that the game will continue is γ
- Then the expected number of rounds is 1/(1 - γ).
Tit for tat
- Finite representation of a unbounded number of rounds
- Copy opponent's previous move thereafter.
Quiz 1: Tit For Tat response to different stratergies
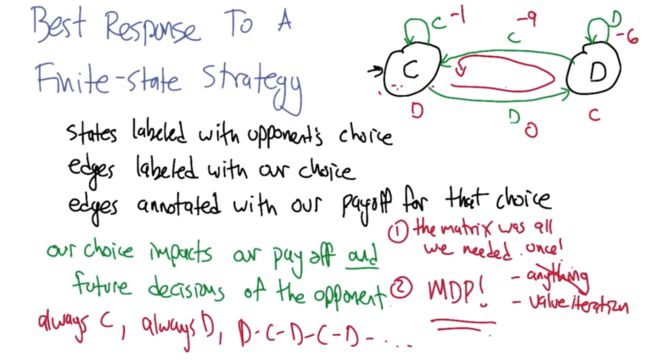
what to do if we Facing TfT?
Quiz2: what should we do against TfT
Finite-state Strategy
- TfT is like an MDP, we can solve TfT by solving MDP
- if our opponent using TfT, then our decision will affect the opponent's decision.
Quiz 3: Response to IPD
Quiz 3 answer
- Playing the game multiple times (unknown times) opens up the possibility of another Nash Equilibrium which is cooperating with each other.
- In this case, both agents playing TfT is a best way to respond to each other.
- But what if γ is not 1/6 here??? or is γ matter?
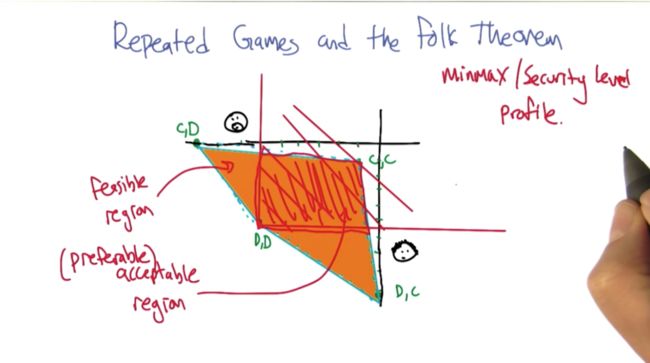
Folk Theorem
Folk Theorem in general MathmaticsX3sA
Folk Theorem in Game Theory
- Describes the set of payoffs that can result from Nash strategies in repeated games.
Quiz 4: Possible average payoff, see next fig for solution
Quiz 4: answer
Minmax Profile and Security level profile
Quiz 5: Minmax Profile
- x is the probability that Smooth chooses "B", Then (1 -x) is the probability that Smooth chooses "S". So Curly will get x if he chooses "B", and 2(1-x) if he chooses "S". Solving x = 2(1-x) will get x.
Security level profile
- MinMax Point: DD point
- Feasible payoff: yellow filled region
- acceptable payoff: any point that to the right-above of MinMax point
- Feasible acceptable payoff: intersection of 1. and 2.
Folk Theorem
Folk Theorem
- Any feasible payoff profile that strictly dominates the minmax/security level profile can be realized as a Nash equilibrium payoff profile with sufficiently large discount factor.
- translation: do what you are told (feasible payoff), or you will be punished (minMax payoff profile). See the next slide for graph representation.
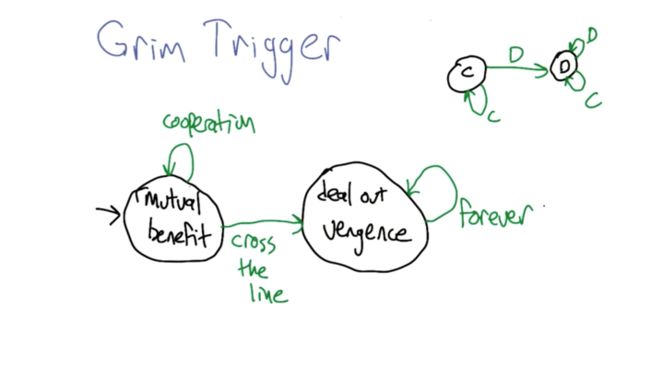
Proof of Folk Theorem
Grim Trigger
- black color--> actions of one agent
- green color--> another agent
- Grim Trigger: once cross line, will always deal with default.
implausible threats
- subgame perfect equilibrium: means taking test response independent of history.
- if under a threat the machine can reach a Nash equilibrium but cannot reach subgame perfect, then it is a implausible threat ( the agent won't carry out the threat)
quiz 6: TfT vs. TfT is not subgame Perfect
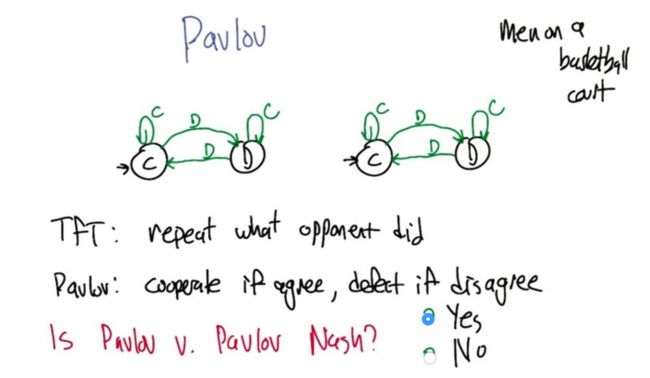
- If #1 is defecting, #2 will get better expected reward if it keeps cooperating instead copying the action of one. SO TfT vs. TfT is NOT subgame perfect.
quiz7: Pavlov Machine
- Pavlov can reach Nash equilibrium if they both choose to cooperate.
Pavlov is subgame perfect
- Pavlov is subgame perfect and reaches NE. So the threat is plausible!
Computational Folk theorem
Stochastic Games and Multiagent RL
Stochastic Games and Multiagent RL
- Game description: A and B are two agents. If they go north, there is a semi-wall with 50% chance of going through. If they both go to the center, they will flip a coin to decide who will take the block. When one agent reach $, game ends and the agent who reaches $ get 100 reward.
- NE exist?: yes, both go center.
Stochastic Games
- Stochastic Games is generalization of both MDP and single agent RL.
Quiz 8: constraining the stochastic game will get other models
- If put some constraints on the stochastic games, we will get some of the games/mdp etc we learned before.
- Since stochastic games are generalized MDP, so we can try to generalize the method to solved the MDP to solve stochastic games.
Zero-Sum Stochastic Games
Zero-Sum Stochastic Games
- Minimax can be used in a Bellman-like equation.
- VI works for the situation, minimax-Q converges, and Q* is unique, policies can be computed.
General-Sum Games
General-Sum Games are not solved
- When we general-sum case, Q type of algorithms will not work.
- The problem is not solved but there are a lot of ideas about =
Possible direction for General Sum Games
Recap
recap
11C Game Theory Revolutions
Game Theory Revolutions
Correlated equilibrium
Chicken Game
- In the chicken game, if both Dare, both get 0 reward (dies), if both chicken, both get 6 rewards. if one dare and the other chicken out, one get 7 and the other get 2 (still alive).
Quiz 1: Nash Equilibrium?
- CC is not NE because if I know you will be C, I will change to D to get more reward.
- CD or DC is NE because C is not willing to change to D, and D is not willing to change to C to get lower rewards.
- DD is not NE because D wants to change to C to get better reward.
- Although CD or DC is NE, but they are not stable because no one wants to always be C to receive a relatively lower reward.
- Mixed Strategy: Dare 1/3 of the time and Chicken out 2/3 of the time. the expected payoff is 14/3.
Quiz 2: Listening to Chris or not?
- Both agents knows three cards [C,C],[CD], and [DC]
- A third person Chris choose a card randomly and inform the agent what to do base on the card. Should the agents listen to Chris?
- if Chris told me to D, then other one must be C. I don't want to change because changing to C will get lower reward.
- if I was told to C, then the other one has half the chance to be C and half the chance to be D. If I choose C, I will get expected reward as 4. If choose D, will get expected reward of 3.5 ( see green words in the next slide). So staying with C is better.
- Yes. and this is called a correlated equilibrium(CE).
Quiz 3: expected payoff of CE
- given [C,C],[CD], and [DC] are randomly chosen, the expected CE is
1/3 * 7 + 1/3 * 2 + 1/3 *6 =5, which is better than 14/3. - not both chicken out to get reward of 6? because [C,C] is not a equilibrium!
- what are the real life analogy of "Chris"? Traffic lights, stop signs……
Correlated Facts
Cooperative-Competitive Values
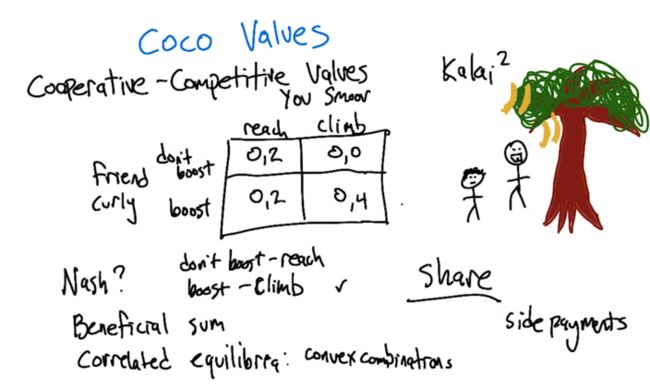
Cooperative-Competitive Values
- There are two N.E in the CoCo game.
- Curly are not motivated to do anything because he always gets 0 in the game. How to motivate him? Side payments? Smooth shares sth with him?
Cooperative-Competitive Values Definition
- to understand this, need to go back and revisit Maxmax, minimax and linear programming.
- the basic idea is to rewrite CoCo into a cooperative part and a competitive part.
CoCo Example
- given an U and U_bar matrix, compute the coco value and side payments.
- calculate maximax and minimax. There are minimax form U's and U_bar's perspective. but the two values can not be values that's outside NE regions.
- Coco value from U and U_bar's perspective are different.
- Side payments can be calculated based on U and U_bar's max value and coco value.
CoCo Recap
- CoCo-Q converges but it is not non-expansion.
Mechanism Design
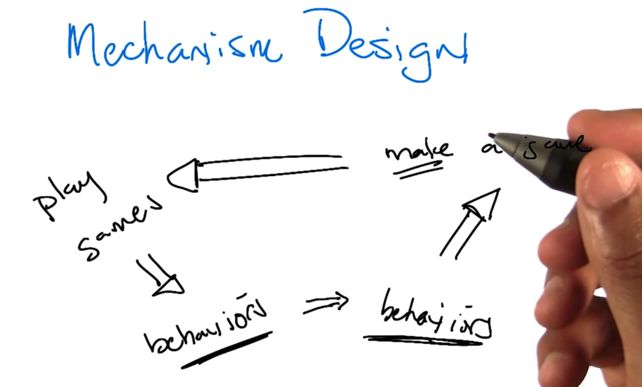
Mechanism Design
- based on wanted behavior to build/make a game.
- E.G. Tax policy to encourage people buying a house
Peer Teaching
- goal: learning.
- Learner get incentives by getting questions correct -> promote learning
- Teacher get incentives by setting the difficulty bar so that if the learning get an easy question wrong and get a hard question correct. -> push student to learn
King Solomon
- in the old King Solomon story, A and B will both say "no" and King will not get no real information.
- Given the mechanism on the left, fake mom will be honest.
- Assumption: the baby's value to real mother and fake mother will be Vreal > Vfake
- ask both the mother, is this your child, if all say yes, then A pays a fine F.
- Then B announce a V that is V > F
- ask the question the same question to A again, if A say yes, A pays V, B pays F and A keeps the baby. if A says no, B keep the baby and B pays V.
Explanation: if B is fake, she will not announce a value that's larger than Vfake, because if A says no, he will get the baby with more than he is willing to pay. So A will get the baby. If B is real mother, she will announce a value Vreal which is larger than Vfake. And A won't say yes because again she will end up with the bay but paying more than she is willing to. So, the real mom will get the baby.
What have we learned.
recap
2015-11-10 初稿
2015-11-17 完成
2015-12-06 reviewed and revised