李宏毅机器学习笔记(四)——分类问题

一.二分类问题

  在二分类中，最终我们要的输出就是两个数值，代表着分到了第一类还是第二类。对比一下我们的回归问题，对于每个点输出的值是在整个实数范围内的，因此分类不能直接的用回归的思想去解决，要另辟蹊径。

1.贝叶斯分类器

  最简单而直观的想法，当然就是转换成对于一个$n$维向量输入，我们去计算它属于这两个类的概率，哪个概率大，就分到哪个类。
  那对于这个$n$维向量输入$x$而言，设这两个类分别是$C_1$和$C_2$，那我们想要计算的，就是$x$在类$C_1$中的概率，即$P(C_1|x)$，之后我们对其用贝叶斯公式展开，可以得到$$P(C_1|x)=\frac{P(C_1)P(x|C_1)}{P(C_1)P(x|C_1)+P(C_2)P(x|C_2)}$$
  那么我们就转换成了求某个类出现的概率和在某个类中$x$的概率。前者非常简单，根据有标签的输入信息统计比例即可，而后者呢？
  一般来说，属于某个类中的那些有标签的点，一般都是有内部规律，符和一种分布的(当然，如果全是纯随机，那谁都没办法分类)。因此，我们就要分两步：(1)假设这个类中的点符合某种分布。(2)在此基础上算出对应的这个分布的参数。一般来说，高斯(正态)分布是最普遍的分布，因此，这里我们就默认这些点符合高斯分布(没错这又是炼丹)。
  我们假设$x$是二维的，我们将属于类$C_1$中的有标签的点可视化，得到下图。

  多元高斯分布的公式如下图所示。

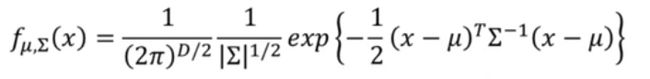
  之后我们对每个类都可以继续使用极大似然估计来计算出对应的参数$\mu$和$\Sigma$，即计算$$L(\mu ,\Sigma ,x_1,x_2,...,x_n)={\Pi }_{i=1}^n{f}_{\mu ,\Sigma }(x_i)$$
  取使得$L$的值最大的参数即可，在这个例子中，我们可以得到$$\mu =\left[\genfrac{}{}{0ex}{}{75}{71.3}\right]$$$$\Sigma =\left[\genfrac{}{}{0ex}{}{874327}{327929}\right]$$
  通过算出的参数，我们就可以计算出$P(x|C_1)$了，从而我们的公式终于可以得到结果了。
  二维情况下的效果如下图所示，正确率甚至不足50%，与随机选差不多；在七维的情况也很一般，只有54%。

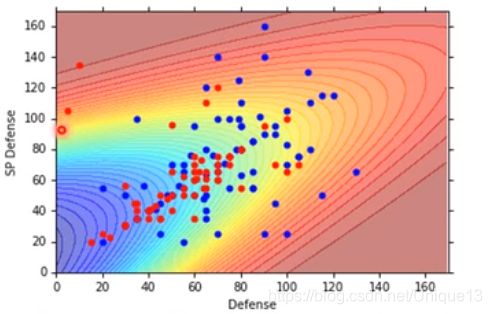
  一般来说，由于这些本就是一个整体，所以很多时候，我们可以理解为所有类的$\Sigma$是同一个值；因此我们可以简化模型，从计算多个$\Sigma$改为计算一个$\Sigma$即可。
  计算的过程其实也是类似，只是改为将所有类合并到一起去用最大似然估计来进行计算，当然最后的结果比较直观：$$\Sigma ={\Sigma }_{i=1}^{n}P(C_i){\Sigma }_i$$  我们带到图里一看，发现恰好是线性的分界线。这不是巧合，我们可以去推所谓的分界线一定是一个超平面(仅仅在二维是一条直线)。

  首先我们可以如下图所示，去将我们的条件概率进行化简，我们可以看出，这时的条件概率已经是一个sigmoid函数了，因此如果这个$z$是关于$x$的线性函数，那么最后的分界线(令这个的概率等于0.5)就一定是一条直线了。

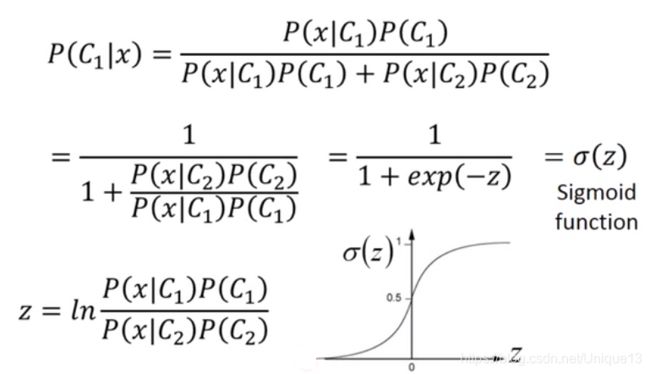
  下面就是对$z$的处理，其实过程就是将ln拆解，再将条件概率展开等等，最后可以得到下图结果。前面虽然这个式子很长，但是我们仔细一看就可以看出，虽然内容复杂，但是结构极其简单，就是$z=w^{T}x+b$这种线性函数。
  因此我们最后的分类的表达式如下:$$P(C_1|x)=\frac{1}{1+e^{-w^{T}x+b}}$$

2.Logistic回归

  在前面的问题中我们可以看出，对于这种线性分类的情况，其实我们就是为了找到最好的参数$w$和$b$而已。上面的方法我们是构建的整体的分布情况，我们完全可以简化方法，不去思考每个类的整体情况，仅仅是直接去计算我们想要的内容，去使用与普通回归类似的方式来学习参数$w$和$b$。
  首先是预测$\hat{y}$，有$P(C_1|x)=f_{w,b}(x)=\sigma (wx+b)$，$\hat{y}=0$当且仅当$f_{w,b}(x)<0.5$，$\hat{y}=1$同理。
  然后下一步就是定义损失函数，我们还是使用最大似然估计。$$L(w,b,x_1,...,x_n)={\Pi }_{x_i在C_1类中}{f}_{w,b}(x_i){\Pi }_{x_i在C_2类中}(1-f_{w,b}(x_i))$$  我们想要这个函数尽量大，我们就相当于是找出让$-lnL$尽量小的参数。仅仅是为了将两种情况合并起来变得好看，我们最后可以得到如下结果:$$w^{\ast },b^{\ast }=\arg \underset{w,b}{\min }(-{\Sigma }_{i=1}^n({\hat{y}}^{i}lnf(x^i)+(1-{\hat{y}}^i)(1-lnf(x^i)))$$  这也就是著名的交叉熵损失函数，可见在logistic回归中我们虽然也是使用了最大似然估计来得到损失函数，但因为其计算方式的不同(这里$f(x)>0.5$则$\hat{y}=1$)，因此得到的结果也不再是均方误差了。
  最后还是使用梯度下降或者Adam等算法即可，还是求损失函数对参数$w$和$b$的导数。忽略掉推导的过程，最后的公式如下图所示。

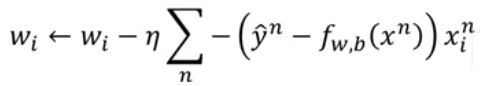
  我们惊奇的发现，这个更新方式竟然和线性回归的公式一模一样，调整的大小与预测值和真实值之间的差距成正比。这也从另一个角度看出了它们在各自问题的合理性。
  而如果我们在这里偏要使用均方误差，即$$L(f)=\frac{1}{2}{\Sigma }_{i=1}^n({\hat{y}}^i-f_{w,b}(x^i){)}^2$$  则$$\begin{array}{rl}\frac{\partial (\hat{y}-f_{w,b}(x){)}^2}{\partial w_i}& =2(\hat{y}-f_{w,b}(x))\frac{\partial f_{w,b}(x)}{\partial z}\frac{\partial z}{\partial w_i}\\ & =2(\hat{y}-f_{w,b}(x))f_{w,b}(x)(1-f_{w,b}(x))x_i\end{array}$$  然而根据上式我们可以看到，如果$f_{w,b}(x)$十分接近于1或者0，那么不论
$\hat{y}$是0还是1，得到的梯度都几乎是0，从而几乎无法进行学习(换句话说，这样无法区分完美正确和完全错误)；没有达到交叉熵的那种，每步移动的大小和到真实解的距离成正比。

3.生成模型vs判别模型

  上面两种方法，前一种是生成模型，后一者是判别模型。
  生成模型中，我们是假设了某种联合分布，之后我们再用这个联合分布来算出我们的条件分布；因此也就是说，我们多做了假设，经过更复杂的计算过程，我们也得到了更多的信息。
  而判别模型中则没有这些，我们直接让机器去自己找条件分布的特征，来预测这个条件分布；从而我们简化了步骤，假设的内容也少了，但是只能得到条件分布的信息，得不到联合分布的信息。
  至于这两种方法孰优孰劣，其实争议也比较大。其实这两大类中都有很多机器学习模型，因此他们显然都是实用的。总的来说，生成模型是否更精确取决于我们对这个联合分布的假设是否与数据契合，然而我们很多时候也不确定是否契合；如果真的很契合，那我们就是相当于多挖掘出了信息，那当然预测的更精确；但是如果数据集中某些类的数据不够多，则会存在着比较大的误差，从而我们的预测就可能比较不准确，从而影响后续的结果。但是，显然生成模型因为多了条件，他的“健壮性”更好，可以更好的免受错误数据和没有标签数据的影响，同时也可以减小后续操作的方差(因为有模型框架的约束)。

二.多分类问题

  基于二分类的思想，我们可以扩展到多分类问题中。

1.选择预测函数

  由于分类数量很多(假设分为m类)，我们无法再通过一个$w$和$b$来计算，将结果再映射；因此我们只能是，我们让$z_i=w_{i}x+b_i$，然后取优化这几组参数，但是下一个问题就是如何去判断$z_i$与$y$之间的相近程度呢？这就出现了一个问题。
  下面是一系列数学内容，高能警告！！

(1).指数族分布

  如果参数为$\eta$，关于$y$的分布为如下图所示的式子，我们就称之为指数族分布。$$p(y;\eta )=b(y)exp({\eta }^{T}T(y)-\alpha (\eta ))$$  当然，这其实是一个比一些著名的分布更广泛的二元函数分布。很多有名的分布，例如指数分布，正态分布，伯努利分布，多项式分布等等等等，都属于指数族分布，这里的证明可见：我是传送门。

(2).广义线性模型假设

  由于指数族分布涵盖了几乎所有的比较常见的分布模型，因此正常来说的线性分类问题，都可以用指数族分布的模型进行建模，通过里面函数的不同来确定模型。然而指数族分布中除了$y$以外只有参数$\eta$，而线性模型中则是${\theta }^{T}x$，因此我们就可以合理的假设${\theta }^{T}x$就是指数族分布的$\eta$。

(3).softmax回归

  对于k分类问题，首先我们要考虑如何表示各输出的概率，这样才可以转化成指数族分布模型。我们当然可以用k个参数${\varphi }_1,{\varphi }_2,...,{\varphi }_k$来对应各输出值的概率，但是，我们完全可以只用k-1个来表示，然后最后一个就是用1去减去其他所有的就可以得到。因此我们有:$$\varphi (i)=p(y=i,\varphi )(1\le i\le k-1)$$$$\varphi (k)=1-{\Sigma }_{i=1}^{k-1}\varphi (i)$$
  之后我们要确定我们的输出如何表示。当然，值一定是有k个，即y=1,2,3,…,k，代表着y属于第几类；当然，为了进行建模，同时将其表示成线性无关的情况，我们就要建立函数$T(y)$。当然，我们这里可以使用k维One-Hot表示法，但为了和上面的输出概率匹配，我们修改为k-1维的变种，即：$$T(1)=[1,0,0,...,0,0{]}_{k-1}^T$$$$T(2)=[0,1,0,...,0,0{]}_{k-1}^T$$$$T(3)=[0,0,1,...,0,0{]}_{k-1}^T$$$$T(k-1)=[0,0,0,...,0,1{]}_{k-1}^T$$$$T(k)=[0,0,0,...,0,0{]}_{k-1}^T$$
  这样也保证了线性无关且有${\Sigma }_{i=1}^{k}T(i)=1$。
  为了更好的进行转化，可以定义一个指示函数$F$,有$F\{statement\}=1$当且仅当$statement$为真；否则$F\{statement\}=0$。因此就有如下式子：$$(T(y){)}_i=F\{y=i\}$$
  之后我们要通过$\varphi$来建立这个模型，我们只要要求不属于第$i$类则为1，否则为${\varphi }_i$，这样就可以保证不管属于哪类，都可以与模型相匹配了。从而$$\begin{array}{rl}p(y;\theta )& ={\varphi }_1^{F\{y=1\}}{\varphi }_2^{F\{y=2\}}...{\varphi }_k^{F\{y=k\}}\\ & ={\varphi }_1^{F\{y=1\}}{\varphi }_2^{F\{y=2\}}...{\varphi }_k^{1-{\Sigma }_{i=1}^{k-1}F\{y=i\}}\\ & ={\varphi }_1^{(T(y){)}_1}{\varphi }_1^{(T(y){)}_2}...{\varphi }_k^{1-{\Sigma }_{i=1}^{k-1}(T(y){)}_k}\\ & =exp((T(y){)}_{1}log({\varphi }_1/{\varphi }_k)+(T(y){)}_{2}log({\varphi }_2/{\varphi }_k)+...+(T(y){)}_{k-1}log({\varphi }_{k-1}/{\varphi }_k)+log({\varphi }_k))\\ & =b(y)exp({\eta }^{T}T(y)-\alpha (\eta ))\end{array}$$  此时有${\theta }^{T}x=\eta =[log({\varphi }_1/{\varphi }_k),log({\varphi }_2/{\varphi }_k),...log({\varphi }_{k-1}/{\varphi }_k)]$,因此有${\varphi }_i=\frac{e^{{\eta }_i}}{{\Sigma }_{j=1}^{k-1}{e}^{{\eta }_j}}$也就是我们的softmax函数。
  最终的效果示例如下所示。也就是说softmax是一种有理有据的建模方式，虽然我们无法证明它是一定最完美的，但是它确实有它统计学的意义，以及现实中优良的效果。

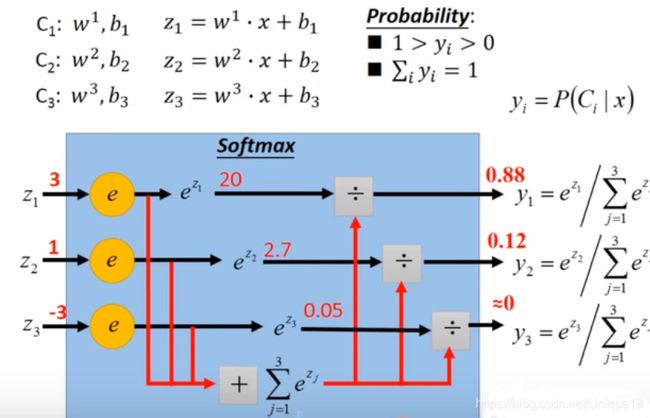
2.计算损失值

  根据上文的One-Hot表示法，对于损失函数我们可以继续采用MLE的思想来做。这里有一个假设，那就是如果分错了类，那么分错到哪类都是一样的，也就是说各个类之间完全独立——这也是合理的，因为One-Hot表示法也是建立在这个前提下的。
  因此对于一个样本的输入，把其他错误的类看成是同一类，带入二分类的表达式中，损失值为$-{\Sigma }_{i=1}^k{\hat{y}}_{i}log{y}_i$,因此直接可以带入到多分类中。对于多个样本就是累加取平均即可。
  有趣的是，这恰好也是信息熵的值，因此也侧面的互相说明了合理性。关于信息熵的概念和计算可以参考如下知乎问题的最高赞回答:https://www.zhihu.com/question/22178202

3.优化

  我们关注损失函数，可以看到这个损失函数最终还是关于$w$和$b$的连续函数，因此可以直接使用梯度下降及其优化算法进行优化，得到损失值最小的解。