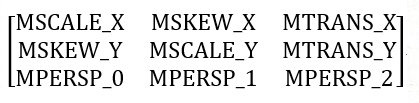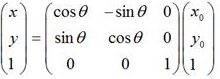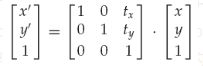图形矩阵-----Matrix

一、矩阵的定义

二、矩阵与矩阵的乘法

矩阵的乘法满足以下运算律：
结合律,分配律,
但是矩阵乘法不满足交换律。
更详细的矩阵知识：
矩阵的运算及其运算规则

三、Matrix---------图形矩阵

1.Matrix 的结构

Matrix 是 Android SDK 提供的一个矩阵类，它代表一个 3 X 3 的矩阵。 Matrix 提供了让我们获得 Matrix 值的 API —— getValues。如果我们将这个 float 排成直观的矩阵格式，那它将是下面这样子的

• 构造函数

public Matrix()
public Matrix(Matrix src)

构造函数有两个，第一个是直接创建一个单位矩阵，第二个是根据提供的矩阵创建一个新的矩阵（采用深copy）。

• isIdentity与isAffine

public boolean isIdentity()//判断是否是单位矩阵
public boolean isAffine()//判断是否是仿射矩阵 

仿射变换其实就是二维坐标到二维坐标的线性变换，保持二维图形的“平直性”（即变换后直线还是直线不会打弯，圆弧还是圆弧）和“平行性”（指保持二维图形间的相对位置关系不变，平行线还是平行线，而直线上点的位置顺序不变），可以通过一系列的原子变换的复合来实现，原子变换就包括：平移、缩放、翻转、旋转和错切。这里除了透视可以改变z轴以外，其他的变换基本都是上述的原子变换，所以，只要最后一行是0,0,1则是仿射矩阵。

• rectStaysRect

public boolean rectStaysRect()

判断该矩阵是否可以将一个矩形依然变换为一个矩形。当矩阵是单位矩阵，或者只进行平移，缩放，以及旋转90度的倍数的时候，返回true。

• reset
  public void reset()
  重置矩阵为单位矩阵。

• setTranslate
  public void setTranslate(float dx, float dy)
  设置平移效果，参数分别是x，y上的平移量。

• setScale
  public void setScale(float sx, float sy, float px, float py)
  public void setScale(float sx, float sy)
  两个方法都是设置缩放到matrix中，sx，sy代表了缩放的倍数，px,py代表缩放的中心。这里跟上面比较类似不做讲解了。

• setRotate
  public void setRotate(float degrees, float px, float py)
  public void setRotate(float degrees)
  例如：
  原图（以下实例的所有原图）：
  

  

  实例的所有原图

//以图片为原点中心，
Matrix matrix = new Matrix();
matrix.setRotate(1, 0, 0, 0);
canvas.drawBitmap(bitmap, matrix, paint);


//以图片为旋转中心，
Matrix matrix = new Matrix();
matrix.setRotate(1, 0, bitmap.getWidth() / 2, bitmap.getHeight() / 2);
canvas.drawBitmap(bitmap, matrix, paint);

图片为原点中心

图片为旋转中心

• setSinCos

public void setSinCos(float sinValue, float cosValue, float px, float py)
public void setSinCos(float sinValue, float cosValue)

sinValue：对应图中的sin值
cosValue：对应cos值
px:中心的x坐标
py：中心的y坐标

setSinCos

如果我们把图像旋转90度，那么90度对应的sin和cos分别是1和0。
看代码如下：

Matrixmatrix = new Matrix();
matrix.setSinCos(1, 0, 0, 0);
canvas.drawBitmap(bitmap, matrix, paint);

-setSkew
public void setSkew(float kx, float ky, float px, float py)
public void setSkew(float kx, float ky)
错切，这里kx，ky分别代表了x，y上的错切因子，px，py代表了错切的中心。

• setConcat
  public boolean setConcat(Matrix a,Matrix b)
  将当前matrix的值变为a和b的乘积

Matrix matrix_a = new Matrix();
matrix1.setValues(new float[]{0.5f, 0, 0, 0, 0.5f, 0, 0, 0, 1.0f});//缩小0.5
Matrix matrix_b = new Matrix();
matrix2.setValues(new float[]{1, 0, 100, 0, 1, 100, 0, 0, 1.0f});//平移100
matrix.setConcat(matrix_a,matrix_b);
canvas.drawBitmap(bitmap, matrix, paint);

注意哦！矩阵a和矩阵b的前乘，后乘是不一样的，如下图可以看到

a * b

b * a

2. 进阶方法解析

Matrix主要用于对平面进行平移(Translate)，缩放(Scale)，旋转(Rotate)以及斜切(Skew)操作。
为简化矩阵变换，Android封装了一系列方法来进行矩阵变换；其中包括：
set系列方法：setTranslate，setScale，setRotate，setSkew；设置，会覆盖之前的参数。
pre系列方法：preTranslate，preScale，preRotate，preSkew；矩阵先乘，如M' = M * T(dx, dy)。
post系列方法：postTranslate，postScale，postRotate，postSkew；矩阵后乘，如M' = T(dx, dy) * M。
通过将变换矩阵与原始矩阵相乘来达到变换的目的，例如：
平移（x'=x+tx；y'=y+ty）

平移

缩放（x'=sx * x；y'=sy * y）

缩放

旋转（x'=cosβ * x-sinβ * y；y'=sinβ * x+cosβ）

旋转

选择需要用到如下的三角函数的公式：
①sin(α+β)=sinαcosβ+cosαsinβ
②cos(α+β)=cosαcosβ-sinαsinβ
公式①可以由单位圆方法或托勒密定理推导出来。
斜切（x'=x+k1 * y；y'=k2 * x+y）

斜切

如下代码：

Matrix matrix = new Matrix();
matrix.setTranslate(100, 1000);
matrix.preScale(0.5f, 0.5f); 

这里matrix前乘了一个scale矩阵，换算成数学式如下：

反之，

Matrix matrix = new Matrix();
matrix.setTranslate(100, 1000);
matrix.postScale(0.5f, 0.5f); 

这里matrix后乘了一个scale矩阵，换算成数学式如下：

实例 1

Matrix matrix = new Matrix();
matrix.preScale(0.5f, 0.5f);//缩放
matrix.preRotate(180);//旋转
//下面的Translate组合是为了将缩放和旋转的基点移动到整个图像的中心，不然系统默认是以图像的左上角作为基点
matrix.preTranslate(-mBitmapWidth()/2, -mBitmapHeight()/2);
matrix.postTranslate(mBitmapWidth()/2, mBitmapHeight()/2);

实例1 效果

实例 2

matrix.reset();
//这段代码的执行顺序：translate(50f, 50f) -> scale(1.5f, 1.5f) -> scale(0.5f, 0.5f) -> translate(50f, 50f)
matrix.preScale(1.5f, 1.5f);
matrix.preTranslate(50f, 50f);
matrix.postScale(0.5f, 0.5f);
matrix.postTranslate(50f, 50f);

公式

实例 2 效果

3.其他方法解析

matrix除了上面的方法外，还有一些其他的方法，
(1) setRectToRect
public boolean setRectToRect(RectF src, RectF dst, ScaleToFit stf)

将rect变换成rect，上面的rectStaysRect已经说过，要保持rect只能做缩放平移和选择90度的倍数，那么这里其实也是一样，只是这几种变化，这里通过stf参数来控制。
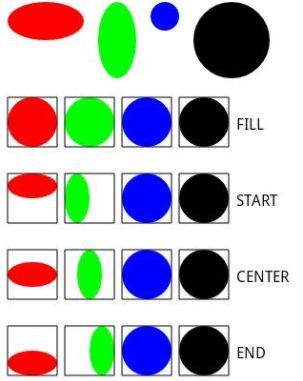
ScaleToFit 有如下四个值：
FILL: 可能会变换矩形的长宽比，保证变换和目标矩阵长宽一致。
START:保持坐标变换前矩形的长宽比，并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。左上对齐。
CENTER: 保持坐标变换前矩形的长宽比，并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。
END:保持坐标变换前矩形的长宽比，并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。右下对齐。
这里使用谷歌的api demo的图片作为例子：

(2) setPolyToPoly
public boolean setPolyToPoly(float[] src, int srcIndex,float[] dst, int dstIndex,int pointCount)
通过指定的0-4个点，原始坐标以及变化后的坐标，来得到一个变换矩阵。如果指定0个点则没有效果。
下面通过例子分别说明1到4个点的可以达到的效果：
1个点-----平移
只指定一个点，可以达到平移效果：

float[] src = {0, 0};
int DX = 100;
float[] dst = {0 + DX, 0 + DX};
matrix.setPolyToPoly(src, 0, dst, 0, 1);
canvas.drawBitmap(bitmap, matrix, paint);

2个点-----旋转或者缩放
两个点，可以达到旋转效果或者缩放效果，缩放比较简单，这里我们来看旋转效果，一个点指定中心，一点指出旋转的效果,代码如下:

int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {bw / 2, bh / 2, bw, 0};
float[] dst = {bw / 2, bh / 2, bw / 2 + bh / 2, bh / 2 + bw / 2};
matrix.setPolyToPoly(src, 0, dst, 0, 2);
canvas.drawBitmap(bitmap, matrix, paint);

图片的中心点作为旋转的中心，前后不变，右上角变化到了下方，所以导致图片旋转了90度。

3个点------错切
使用3个点，可以产生错切效果，指定3个顶点，一个固定，另外两个移动。 代码如下：

Matrix matrix = new Matrix();
int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {0,0, 0, bh,bw,bh};
float[] dst = {0, 0, 200, bh, bw + 200, bh};
matrix.setPolyToPoly(src, 0, dst, 0, 3);
canvas.drawBitmap(bitmap, matrix, paint);

4个点------透视
透视就是观察的角度变化了。导致投射到平面上的二维图像变化了。

Matrix matrix = new Matrix();
int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {0, 0, 0, bh, bw, bh, bw, 0};
int DX = 100;
float[] dst = {0 + DX, 0, 0, bh, bw, bh, bw - DX, 0};
matrix.setPolyToPoly(src, 0, dst, 0, 4);
canvas.drawBitmap(bitmap, matrix, paint);

可以看到，只是把左右两个顶点往里面收拢了，这样就得出了一个有3d效果的透视图。
(3) invert
public boolean invert(Matrix inverse)

反转当前矩阵，如果能反转就返回true并将反转后的值写入inverse，否则返回false。当前矩阵inverse=单位矩阵。
反转前后有什么效果，我们来看看示例：

可以看到，反转之后，其实是对效果的一种反转。

(4) mapPoints

public void mapPoints(float[] dst, int dstIndex, float[] src, int srcIndex,int pointCount)
public void mapPoints(float[] dst, float[] src)
public void mapPoints(float[] pts)

映射点的值到指定的数组中，这个方法可以在矩阵变换以后，给出指定点的值。
dst：指定写入的数组
dstIndex：写入的起始索引，x，y两个坐标算作一对，索引的单位是对，也就是经过两个值才加1
src：指定要计算的点
srcIndex：要计算的点的索引
pointCount：需要计算的点的个数，每个点有两个值，x和y。
(5) mapVectors

public void mapVectors(float[] dst, int dstIndex, float[] src, int srcIndex,int vectorCount)
public void mapVectors(float[] dst, float[] src)
public void mapVectors(float[] vecs)

与上面的mapPoionts基本类似，这里是将一个矩阵作用于一个向量，由于向量的平移前后是相等的，所以这个方法不会对translate相关的方法产生反应，如果只是调用了translate相关的方法，那么得到的值和原本的一致。
(6) mapRect
public boolean mapRect(RectF dst, RectF src)
public boolean mapRect(RectF rect)
返回值即是调用的rectStaysRect()，这个方法前面有讲过，这里把src中指定的矩形的左上角和右下角的两个点的坐标，写入dst中。
(7) mapRadius
public float mapRadius(float radius)

返回一个圆圈半径的平均值，将matrix作用于一个指定radius半径的圆，随后返回的平均半径。