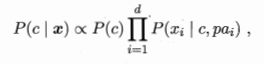《机器学习（周志华）》学习笔记（七）

Q：什么是贝叶斯分类器？

一句话：以贝叶斯方法为核心原理构造出来的分类程序统称为贝叶斯分类器，主要包括朴素贝叶斯分类器，半朴素贝叶斯分类器，以及贝叶斯网络。

Q：那么，贝叶斯方法又是什么？

贝叶斯方法是一位英国数学家托马斯·贝叶斯在18世纪提出来的概率学方法。此法强大之处不多赘述，贝叶斯学派占据了概率江湖中的半壁江山（另外一半江山归于频率学派）。

举个例子：

已知
——100名男生中有99个短发，1个长发；
——100名女生中有90个长发，10个短发；

那么
——从这200名学生中抽取一个学生，已知是男生，则该男生是长发的概率是多少？答案很简单，是0.01000。

——从中200名学生中抽取一个学生，已知是长发，则该长发学生是男生的概率是多少？答案稍难一点，是0.01099。

由此可见，大多数的概率计算方法（古典概率模型、几何概率模型、条件概率公式、全概率公式、联合概率公式······）都是已知前提条件发生的情况下求各种可能结果发生的概率。而贝叶斯公式则是用于已知一件事情已经发生，求导致其发生的各种可能前提条件成立的概率。

已知：A => a 或 b 或 c 求P(a)
用古典概率模型、几何概率模型、条件概率公式、全概率公式、联合概率公式······

已知：A 或 B 或 C => a 求P(A)
用贝叶斯公式

更多贝叶斯方法的知识，可以查阅刘未鹏《数学之美番外：贝叶斯方法》

Q：怎样应用贝叶斯方法构造分类器？

我们继续以西瓜分类问题为例，用下面的色泽、根蒂等8个特征的数据，判断一个西瓜是好瓜还是坏瓜。

西瓜数据集3.0

应用贝叶斯方法的基本思想是，分别求出待分类西瓜是好瓜以及坏瓜的概率，哪一个概率高，就将其归到那一类。

那么

这两个概率怎么求？

首先我们假设样本的所有属性相互独立，比如西瓜的色泽是黑是绿，与根蒂是直是曲无关。则根据贝叶斯方法，求一个西瓜是好瓜还是坏瓜的概率的基本公式是如下

其中c是类别，向量是待测样本。因为我们并不需要求出的确切值，只需要知道和谁更大就行。因为分母P(x)对于和是一样的，所以可以一并舍去。所以关键要求出P(c)以及P(x|c），也就是

亦即

这两条式子中基本上每一项都是一个简单的条件概率。对于离散型变量，一般情况下可以直接用数数的方法加古典概型算出来。

数据集中的密度和含糖率是连续型变量，他们的条件概率怎么求？可以假设这些连续数据服从正态分布，然后算出训练数据集中这两项属性的均值和方差，代入下面概率密度函数，即可算出。

用训练数据集算出各个特征的条件概率以及各个类别出现的概率以后，就可以应用贝叶斯公式预测一个西瓜是好瓜以及坏瓜的概率了。

在上面的例子中，我们

用到了贝叶斯公式
假设各个属性互不影响（实际上不是，比如敲声可能受密度影响）

所以我们刚刚构造出的分类器叫做朴素贝叶斯分类器(Naive Bayesian classifier)。

Q：我觉得朴素贝叶斯分类器太Naive，想要高逼格一点，如何改进？

虽然朴素贝叶斯算法很Naive，但是实践显示其性能很已经不错，尤其是在文本分类领域有广泛应用，很多垃圾邮件分类算法用的就是朴素贝叶斯。

当然，可以不Naive一点，用半朴素贝叶斯（semi-naive Bayesian classifier）。

朴素贝叶斯， naive之处在于假设各个属性互不影响。这在实践中不易见到，所以人们尝试放宽点这个条件，比如改成“假设各个属性最多受一个属性影响（最多依赖于一个属性）”。

如此一改，整个模型就由

变成了

两条式子的唯一的不同之处在于各个条件概率项的条件部分，pa_i指的是被依赖的属性。举个例子——若敲声受密度影响，则有

P(敲声=沉闷|好瓜=是，密度>0.700)
P(敲声=沉闷|好瓜=否，密度>0.700)
P(敲声=沉闷|好瓜=是，密度<=0.700)
P(敲声=沉闷|好瓜=否，密度<=0.700)
······
除此之外，其他与朴素贝叶斯无大出入。

Q：半朴素贝叶斯中还是有点naive，有没有不naive的贝叶斯算法？

当然有，比如贝叶斯网络（Bayesian network），又称信念网络（Belief network）,也就是当我们完全放开了“属性之间相互影响”的假设的时候，所诞生的算法。此时一个属性可以影响多个其他属性，也可以受多个属性影响，这就比朴素贝叶斯和半朴素贝叶斯复杂多了。

贝叶斯网络之间的属性的影响关系，可以用一个有向无环图描述，图中每一个节点存储着该属性的条件概率。如

所以一个贝叶斯网络由一个有向无环图和一个条件概率表组成。

贝叶斯网络是相当高级和复杂的技术，目前我还没有全面理解，在此留白，等以后有机会再来补充。

Talk is cheap, show me the code!

使用朴素贝叶斯算法计算离散型和连续性变量时求条件概率的方法略有不同，但方便起见，我还是将其完全拆开放到两个模型里。首先时离散型变量的朴素贝叶斯模型：

"""
Naive Bayes classifier for categorical variables

:file: supervised.py
:author: Richy Zhu
:email: [email protected]
"""
import numpy as np

class MyCategoricalNBC:
    '''categorical naive bayes classifier'''

    def __init__(self):
        self.X = None
        self.y = None

    def fit(self, X, y):
        '''
        Train the nominal naive bayes classifier model

        Parameters
        ----------
        X: ndarray of shape (m, n)
            sample data where row represent sample and column represent feature
        y: ndarray of shape (m,)
            labels of sample data

        Returns
        -------
        self
            trained model
        '''
        self.X = X
        self.y = y
        return self
    
    def _predict(self, x):
        '''
        compute probabilities and make prediction.
        '''
        probas = {}
        clss = list(set(self.y))

        # compute probability for each attributes in x
        for c in clss:
            probas[c] = []
            dat = self.X[self.y==c]
            for attr_id, attr_val in enumerate(x):
                count = 0
                for row in dat:
                    if attr_val == row[attr_id]:
                        count += 1
                # use laplace smoothing
                probas[c].append((count+1)/(len(dat)+len(x)))
            probas[c].append(len(dat)/len(self.X))

        final_probas = {}
        from functools import reduce
        for c, prbs in probas.items():
            # theoretically not final probability because not divided by Pr(x)
           final_probas[reduce(lambda x,y:x * y, prbs)] = c
        return final_probas[max(final_probas)]
    
    def predict(self, X):
        '''
        Make prediction by the trained model.

        Parameters
        ----------
        X: ndarray of shape (m, n)
            data to be predicted, the same shape as trainning data

        Returns
        -------
        C: ndarray of shape (m,)
            Predicted class label per sample.
        '''
        if self.X is None:
             raise Exception("Model haven't been trained!")
        return np.array([self._predict(x) for x in X])

测试代码如下——因为sklearn包没有离散变量的数据集，又不想动用新闻数据集（其实是我的代码处理不了，会出bug），所以只能将就着用一下重复10次的西瓜数据集：

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

print('\nDescrete Naive Bayes')
print('---------------------------------------------------------------------')
xigua2 = np.array([
        ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],
        ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],
        # ----------------------------------------------------
        ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],
        ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],
        ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],
        ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],
        ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],
        ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']
    ])
from sklearn.preprocessing import LabelEncoder
for i in range(xigua2.shape[1]):
    le = LabelEncoder()
    xigua2[:,i] = le.fit_transform(xigua2[:,i])
xigua2 = xigua2.astype(np.int).repeat(20, axis=0)
X = xigua2[:, :-1]
y = xigua2[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y)

mycnb = MyCategoricalNBC()
mycnb.fit(X_train, y_train)
print('My Accuracy:', accuracy_score(mycnb.predict(X_test), y_test))

from sklearn.naive_bayes import CategoricalNB 
skcnb = CategoricalNB()
skcnb.fit(X_train, y_train)
print('SK Accuracy:', accuracy_score(skcnb.predict(X_test), y_test))

测试结果如下

$ python supervised_examples.py
Descrete Naive Bayes
---------------------------------------------------------------------
My Accuracy: 0.8235294117647058
SK Accuracy: 0.8235294117647058

下面是处理连续型变量数据集的朴素贝叶斯模型（假设所有连续变量都服从高斯分布）：

"""
Naive Bayes classifier for continuous variables

:file: supervised.py
:author: Richy Zhu
:email: [email protected]
"""
import numpy as np
class MyGaussianNBC:
    '''Gaussian continuous naive bayes classifier'''

    def __init__(self):
        self.X = None
        self.y = None

    def fit(self, X, y):
        '''
        Train the Gaussian continuous naive bayes classifier model

        Parameters
        ----------
        X: ndarray of shape (m, n)
            sample data where row represent sample and column represent feature
        y: ndarray of shape (m,)
            labels of sample data

        Returns
        -------
        self
            trained model
        '''
        self.X = X
        self.y = y
        return self

    def _predict(self, x):
        '''compute probabilities and make prediction.'''
        from scipy.stats import norm
        probas = {}
        clss = list(set(self.y))

        # compute probability for each attributes in x
        for c in clss:
            probas[c] = []
            dat = self.X[self.y==c]
            for i, attr in enumerate(x):
                probas[c].append(norm(np.mean(dat[:,i]), np.std(dat[:,i])).pdf(attr))
            probas[c].append(len(dat)/len(self.X))

        final_probas = {}
        from functools import reduce
        for c, prbs in probas.items():
            # theoretically not final probability because not divided by Pr(x)
           final_probas[reduce(lambda x,y:x * y, prbs)] = c
        return final_probas[max(final_probas)]
    
    def predict(self, X):
        return np.array([self._predict(x) for x in X])

测试代码如下

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

print('\nContinuous Naive Bayes')
print('---------------------------------------------------------------------')
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y)

mygnb = MyGaussianNBC()
mygnb.fit(X_train, y_train)
print('My Accuracy:', accuracy_score(mygnb.predict(X_test), y_test))

from sklearn.naive_bayes import GaussianNB
skgnb = GaussianNB()
skgnb.fit(X_train, y_train)
print('Sk Accuracy:', accuracy_score(skgnb.predict(X_test), y_test))