PRML读书会第十二章 Continuous Latent Variables（PCA，Principal Component Analysis，PPCA，核PCA，Autoencoder，非线性流形）

主讲人 戴玮

（新浪微博: @戴玮_CASIA）

Wilbur_中博(1954123) 20:00:49 

我今天讲PRML的第十二章，连续隐变量。既然有连续隐变量，一定也有离散隐变量，那么离散隐变量是什么？我们可能还记得之前尼采兄讲过的9.2节的高斯混合模型。它有一个K维二值隐变量z，不仅只能取0-1两个值，而且K维中只能有1维为1、其他维必须为0，表示我们观察到的x属于K类中的哪一类。显然，这里的隐变量z就是个离散隐变量。不过我们容易想到，隐变量未必像kmeans或GMM这种聚类算法那样，非此即彼、非白即黑，我们当然也可能在各个聚类或组成成分之间连续变化。而且很多情况下，连续变化都是更合理、更容易推广的。所以，我们这一章引入了连续隐变量。
书中举了一个例子：从某张特定的手写数字图像，通过平移和旋转变换生成多张图像。虽然我们观察到的是整个图像像素的一个高维数据空间中的样本，但实际上只是由平移和旋转这三个隐变量产生的，这里的平移和旋转就是连续隐变量。还举了个石油流量的例子，是从两个隐变量经过测量得到12个观察变量，那里的两个隐变量也是连续的。 一般来说，样本不会精确处在由隐变量表示的低维流形上，而是可能稍有偏差，这种偏差可视作噪声。噪声的来源各种各样，不是我们能把握的，一般只能统一把它们看成单一的噪声项来处理。
最简单的情况下，我们可以把隐变量和观察变量都假设为高斯分布，并且利用2.3.1讲过的条件分布与边缘分布之间的线性高斯关系，来建立观察变量与隐变量之间的线性模型。这样，我们就可以建立主成分分析（PCA）以及与之相关的因子分析（FA）的概率模型。不过在此之前，我们还是看看传统视角是如何处理主成分分析的：
PCA也叫Karhunen-Loève transform（KL变换）或Hotelling transform（霍特林变换）。它有两种可产生相同算法的等价视角：最大方差和最小重构误差。两种视角都希望找到一组正交投影，把原数据投影到低维的线性子空间上。但最大方差视角是说，我们希望数据投影之后在投影方向上有最大方差；而最小重构误差视角是说，我们希望投影后的数据和原数据之间的均方差最小。前者由Hotelling于1933年提出，后者由Pearson于1901年提出。
先来看最大方差视角。首先定义样本均值和样本协方差：


然后，我们可以得到某个投影方向u_1上的方差：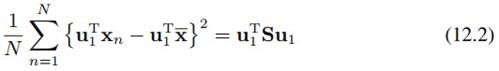

不失一般性，我们令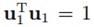，这样我们就可以将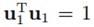作为约束，将方差最大作为目标函数，把这个问题看作有约束最优化问题，因此可用拉格朗日乘子法求解：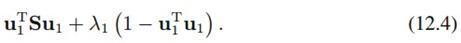

令其导数为0，可得到：
 
这是我们熟悉的线性代数中的特征值分解问题，lambda_1和u_1分别是S的特征值和特征向量。而且可以看到，这里求出的u_1方向的最大方差就是：

在余下的方向中依次选择最大方差方向，就是S由大到小给出的各个特征值以及对应的特征向量，这也容易从S是实对称矩阵、因此得到的特征向量之间是正交的这一点看出来。
再来看最小重构误差视角，由投影方向之间的标准正交关系，我们可以得到样本在D个投影方向下的表示：

但我们不想用D个投影方向，而是想用M<D个方向来表示样本，并且希望这样表示尽可能接近原样本。那么原样本与M个方向重构得到的样本之间的误差，用均方差来衡量就是：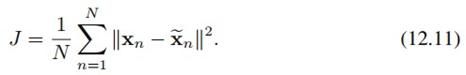

上面的公式12.14展开之后就是：

我们想最小化这个重构误差项。因为投影方向之间正交，所以也可以逐一求解，也就是目标函数：

约束条件是：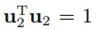

同样可以由拉格朗日乘子法得到：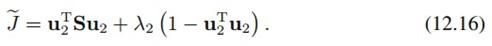

这和最大方差视角一样，也是特征值问题。只不过这里是去掉较小特征值对应的方向，因为那些方向对应着较小的重构误差，而先前是保留较大特征值对应的方向。但得到的结果是完全一样的。
在D个特征向量中选择前M个作为投影方向，得到的重构误差就是：
 
下面简单谈谈PCA的复杂度问题。我们知道，S是DxD维矩阵，对S做特征值分解需要O(D^3)的复杂度。如果仅需要前M个最大的特征值以及特征向量，那么有一些算法可达到O(M*D^2)复杂度，比如power method(Golub and Van Loan, 1996)。然而，即使是O(M*D^2)，在D较大的时候也是难以接受的。比如我们可能会用PCA做人脸识别的一些处理，人脸图像一般是几万维的，那么O(M*D^2)就是至少好几亿的复杂度，这显然是无法接受的。一会我们要讲的概率角度下用EM算法求解PPCA可以进一步降低复杂度。但仅从矩阵分解角度，实际上有一个非常巧妙的方法，也是PCA实现中常用的一种技巧：

我们知道，对S做特征值分解的公式是：

我们可以把左右都左乘X，得到：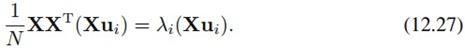

令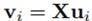得到：

这里可以看到，对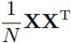做特征值分解，与对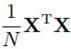做特征值分解，它们有着相同的非零特征值，但特征向量是不一样的。

不过，对(12.28)左右同时左乘X^T之后，我们可以得到：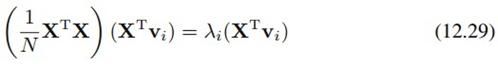

则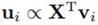 
因为我们要求投影方向是标准正交的，所以归一化之后就是

因为XX^T是NxN矩阵，和样本数量相关而和特征维度无关，所以如果是特征空间维度很高，但样本数量相对来说不那么大，那么我们就可以对XX^T做特征值分解，而不是X^TX。这样算法求解起来会快很多。但是，如果样本数量也很大、特征维度也很高，这样做也不合适了。这时就需要借助概率模型来求解。

============================讨论=================================

Wilbur_中博(1954123) 20:30:56 
好了，有问题现在可以提问。
dxhml(601765336) 20:32:36 
好像还没看出和连续隐变量的关系，是不是数据在主成分方向的投影是隐变量，因为是连续的，所以。。。
Wilbur_中博(1954123) 20:33:35 
嗯，还没讲到连续隐变量。。前面说了，这是传统视角的PCA，而不是一会要讲的概率视角。 概率视角才有隐变量观察变量那套东西。

我觉得这部分应该都蛮熟悉的，不会有什么问题吧。
Phinx(411584794) 20:34:46 
为什么维度太高了，就不合适啊？
coli<[email protected]> 20:35:19 
现在应该是理论阶段吧
布曲(15673189) 20:35:22 
矩阵运算太复杂了
Wilbur_中博(1954123) 20:36:11 
因为O(D^3)里的D就是维度，太高了矩阵分解很慢，就算是O(D^2)也够慢的。前面说了，上万维的图像，一平方就好几亿了。
也不是理论阶段了，其实那个把DxD变为NxN的技巧就很实用的。没什么问题就继续了哈
布曲(15673189) 20:37:54 
是的 大家可以去网上下pca人脸识别的matlab小代码

========================讨论结束=================================
Wilbur_中博(1954123) 20:40:45 
前面讲的传统视角，是把原数据空间往较低维子空间上做线性投影，找这个投影方向。下面，我们从概率角度、用隐变量来建模。PCA也可以从这种角度导出。PPCA相较于传统PCA，有以下优点：
1. 既可以捕捉数据中的线性相关关系，又可以对高斯分布中的自由参数加以限制；
2. 在少数几个特征向量的特征值较大、其他都较小时，用EM算法求解PCA是很高效的，而且它不用计算协方差阵作为中间步骤；
3. 概率模型和EM的结合，使我们可以解决数据集中的missing values；
4. PPCA的混合模型也可用EM求解；
5. 贝叶斯方法可自动确定数据的主子空间维度；
6. 它的似然函数可以有概率解释，因此可与其他概率密度模型做比较；
7. PPCA可作为类条件概率用到分类器中；
8. 可从中采样得到新样本。
PPCA是前面2.3.1讲过的线性高斯模型的一个实例。线性高斯模型就是说，边缘分布是高斯的，条件分布也是高斯的，而且条件分布的均值与边缘分布之间是线性关系。这里我们引入隐变量z及其分布p(z)，并且观察变量x是由z产生的，因此有条件分布p(x|z)。
不失一般性，设z服从0均值单位方差的高斯分布，则有：
以及

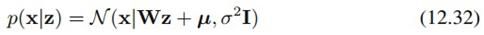
这里的参数有三个：从隐变量空间到观察变量空间的线性变换W、均值mu和方差sigma^2。从产生式的观点来看，我们先从p(z)采样得到隐变量z的值，然后用这个值经过线性变换，并加上均值项（可看做一个常数偏移）和高斯噪声项，就可以得到x：

这里z是M维高斯隐变量，epsilon是D维零均值高斯分布噪声，且有方差sigma^2*I，也就是说，我们假定各维噪声之间是独立的、且方差相等。从这个概率框架可以看出，我们先是用W建立了隐变量与观察变量之间的关系，再用mu和epsilon描述了观察变量的概率分布是什么样的。
我觉得PPCA比起传统PCA，有一点优势就是利用了概率分布。因为我们的数据即使在某个低维子空间上，也不可能分布在整个子空间，而是只处在其中一个小区域。概率模型就很好地利用了这一点。当然，除了生成数据之外，概率模型更大的优势还是通过观察变量，也就是手里的数据，去推断参数也就是W、mu、sigma^2是什么。这就要利用一些统计推断方法，比如最大似然法。但想用最大似然，必须先知道似然函数是什么。由2.3.1, 2.3.2, 2.3.3这几节的锤炼，我们应该对高斯分布的边缘分布、条件分布等形式的推导已经很熟练了。所以我们从前面给出的p(z)和p(x|z)，容易得到边缘分布p(x)：

其中

实际上把(12.31)和(12.32)的协方差，代入到2.3.3最后给出的边缘分布公式中，可以得到这里给出的边缘分布p(x)。当然也可以像书上讲的那样，从(12.33)来推导。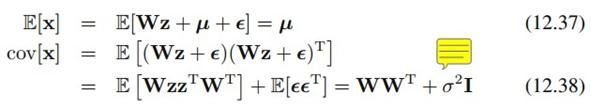
 
因此我们得到了似然函数的具体形式：它也是一个高斯分布，以及它的期望和协方差是什么。高斯分布的指数里有协方差的逆，这里协方差矩阵C是DxD维的：

所以直接求逆的话复杂度也很高。我们也可以利用一些技巧，把直接求逆的O(D^3)复杂度降到O(M^3)


有了似然函数，我们就可以用最大似然法来从观察变量求解未知参数了。首先，为了方便求解，我们对似然函数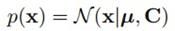取对数，这是我们都很熟悉的做法了，得到：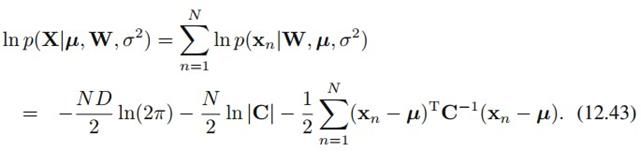

前面说过，我们的未知参数有三个：W, mu, sigma^2，似然函数逐一对它们求导，令导数为0，就可以得到各自的参数估计。
mu的形式最简单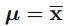代回(12.43)得到：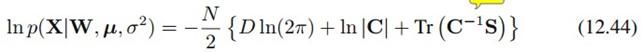

这里利用了sum(x_i^T*S*x_i) = Tr(X^T*S*X)，其中X的第i列是x_i，这是因为X'SX的第(i,j)个元素等于X'的第i行乘以S乘以X的第j列。因此，(12.43)的最后一项可变为(12.44)的最后一项。还要利用trace的性质：Tr(ABC) = Tr(BCA) = Tr(CAB)。
但对剩下的两个参数求导以及求解的过程，这里就比较含糊其辞了，只是说求解比较复杂，但仍然可以得到解析解。 直接给出书上写的解析解形式：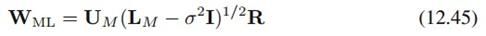

这里的U_M由S（样本协方差阵）的最大的M个特征值对应的特征向量组成时，可以取到最大值，如果不是最大的而是任意特征向量，那么只是鞍点，这是由Tipping and Bishop (1999b)给出的证明。L_M是相应特征值的对角阵，而R是任意的MxM维旋转矩阵。 因为有R的存在，所以可以认为，从概率角度看，这些隐变量张成的子空间以及从该子空间如何生成样本比较重要，但取这个子空间的哪些方向则不是那么重要。只要子空间一致，我们可以任意旋转张成子空间的这些方向。我觉得这也是PPCA和传统PCA的区别之一。
sigma^2的最大似然解是：
 
直观来看，它的物理意义是，被我们丢弃的那些维度的方差的平均值。从(12.32)和(12.33)看到，sigma^2实际上代表了噪声的方差，那么这个方差当然是越小越好，说明W已经尽可能保留了分布信息。它也可以看成某种平均重构误差。
你们可以先讨论讨论。。看看有什么问题

dxhml(601765336) 21:36:52 
这样的模型的表达能力有限，X如果不是高斯分布呢？
Wilbur_中博(1954123) 21:40:43 
@dxhml 是啊，所以这是最简单的模型，肯定还是要由浅入深么。后面还会讲到高斯分布之外的假设。

继续，既然给出了解析形式，那么我们仍然可以用特征值分解的方法来求解，因为W和sigma^2的最大似然估计都是和特征值以及特征向量相关的。但因为有似然函数，所以借助各种最优化工具，比如共轭梯度法，或者一会要讲到的EM，求解起来会更快。这一小节最后还讲到了PPCA因为建立了隐变量与观察变量之间的关系，所以自由度上远比直接估计高斯分布要小，这样估计起来所需要的数据也就小不少，速度也会快很多。
下面讲PPCA的EM求解，EM法有这样几个好处：高维空间下比解析解速度快，可扩展到其他没有解析解的模型比如因子分析（FA）上，可处理missing data的情况。EM法尼采兄前面已经讲得很清楚了，就是在E、M两步间来回迭代。这里因为我们在E步求出z_n和z_n*z_n^T的后验期望，然后在M步把这两个期望代回去，就可以做对数似然的最大化了，然后可以得到新的W和sigma^2。
前面我们看到，mu的形式非常简单，所以mu就直接用样本均值代替了，迭代求的只有W和sigma^2。也就是：

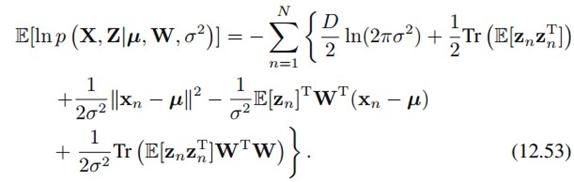
其中E步：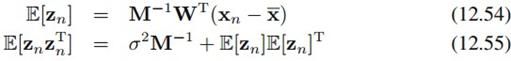
M步：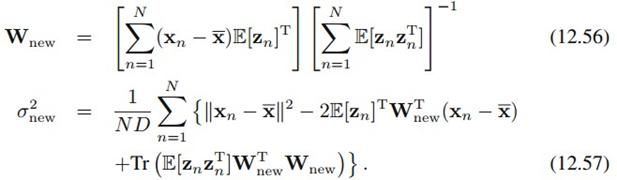

EM法并不需要显式构造协方差阵，它的主要开销在于W和sigma^2的更新中对整个数据集做求和操作，所以复杂度是O(NDM)，可以看到，因为高维情况下D比较大，而我们降维后的维度M较小，所以比特征值分解最好的O(ND^2)要好不少。而且EM的online版本可以进一步提高效率。missing data就不讲了。。自己看看吧。

==========================讨论=================================

布曲(15673189) 22:07:20 
ppac优于传统的pca主要是因为运算速度吗，因为引入隐变量 可以用em更快的求解?
Wilbur_中博(1954123) 22:10:20 
嗯，我觉得运算速度上是有优势的，因为特征值分解比较耗时。不过传统角度应该也可以用一些最优化方法和online方法求解那个代价函数吧。没有具体总结过。感觉更大的优势还是在概率角度解释数据比较好。前面我说过一个：我觉得PPCA比起传统PCA，有一点优势就是利用了概率分布。因为我们的数据即使在某个低维子空间上，也不可能分布在整个子空间，而是只处在其中一个小区域。概率模型就很好地利用了这一点。
布曲(15673189) 22:12:12 
嗯 同意
Wilbur_中博(1954123) 22:12:14 
我觉得这可能是比较有优势的。传统PCA投影角度感觉解释得有点粗糙了。是吧。
========================讨论结束=================================

Wilbur_中博(1954123) 20:57:53 
从12.2.3继续讲，上次我们看到了怎么从贝叶斯角度解释PCA，也就是PPCA。简单说，就是假设有个隐变量z服从标准高斯分布，它通过某个线性变换W生成x，这个变换过程还可能有某些未知的随机因素比如噪声等，可将其假设为0均值同方差随机变量。所以，我们要做的就是通过手里拿到的数据X去推断未知参数：线性变换W、偏移量同时也是x的均值mu、未知随机量的方差sigma^2*I。这里W的各列张成了我们感兴趣的主成分空间。我们讲到，虽然通过最大似然解得到的W与原先传统PCA相比，求出来的主方向差不多，但用EM法求解复杂度降低了不少，而且从贝叶斯角度也可以对PCA的模型假设和生成过程有更深刻的认识。但有一个问题我们没有谈到，就是如何选择W中的哪些主方向是最有用的，或者说如何更有效地降维。

我们上次讲过，从(12.45)：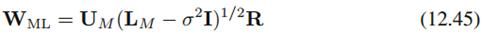

可以看到，它的最大似然解仍然与最大的那些特征值以及对应的特征向量相关，所以我们也可以像传统PCA那样，把特征值从大至小排列出来，看看是不是在哪个值上突然下降，把特征值分成较大和较小的两部分，那么我们就可以选择较大的那部分特征值以及与其对应的特征向量。
但是，一方面，特征值未必存在这种突然下降的趋势，可能是比较平滑地逐渐下降；另一方面，我们既然用了贝叶斯方法，那就应该将贝叶斯进行到底。
我们在第7章也讲过，用某些先验可以将特征的线性表示稀疏化，进而起到特征选择的效果，那么这里，我们也可以利用这一思想做降维。既然用贝叶斯，那就肯定要对W设一个先验分布。这里介绍了一种比较简单的方法：设W的先验分布为各维独立的高斯分布，且各维方差由precision超参数alpha_i控制，前面讲过，precision就是方差的倒数。那么，先验分布可以写作：

稍后可以看到，alpha_i在迭代计算的过程中，有些会趋向于无穷大，那么相应地，那个维度的w_i就会趋向于0，说明那个维度的特征没什么用。这样我们有用的特征就是alpha有限的那些维度，而且alpha越小的维度越有用。这是比较常见的稀疏化方法，更具体的内容可参见PRML的7.2节。求解方法就是一般贝叶斯求解的EM法，首先把W积掉，得到似然函数：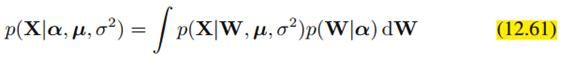

这个边缘分布的积分是不易求的，我们可以借助前面讲过的4.4节的Laplace approximation，对alpha_i求边缘分布的极值，得到：

这是EM当中M步的估计alpha_i的计算公式。
M步估计sigma^2的公式和先前PPCA的EM法讲过的(12.57)一样，而W的公式涉及到先验，所以稍有改变：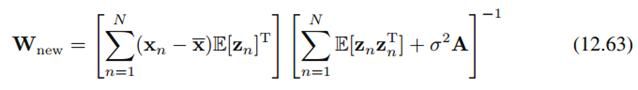

E步的公式没有变化。
这样经过多次迭代之后，就可能有某些alpha_i会趋向于无穷大，我们就可以把那些方向去掉。当然，我们也可以进一步去掉那些较大的alpha_i，只留下较小的。不过一般来说去掉无穷大的那些已经足够了。下面是分别使用前面讲过的EM法和这里讲的带有稀疏化效果的EM法的图示，可以看到，降维效果是十分明显的：

下面看一下12.2.4的因子分析FA，FA和之前PPCA的不同在于，PPCA的条件分布是：

而FA是：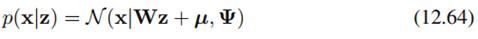

求解方法什么的也都差不多。这里就不多讲了。说实话我对FA不理解得并不深，而且这里讲的FA和我之前理解的FA似乎也不太一样。我原先以为FA就是类似于PCA，各方向可任意旋转，不一定是特征值从大到小排列的那种，但各方向之间仍保持正交。不知道大家是怎么看FA的？

下面重点讲一下12.3 核PCA（KPCA）：

第六章讲过，我们可以方便地把内积扩展到非线性核，从而可以利用它来隐式求解非线性情况。这里，我们也利用核方法来求解PCA。因为要利用内积的非线性核，所以我们必须把传统PCA以内积方式表示出来。前面讲过，传统PCA是求样本协方差阵的特征值与特征向量：

样本协方差阵是DxD维的：

并且特征向量有约束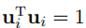
现在我们利用非线性变换phi把样本变换为，暂时为了方便假定变换后的向量有0均值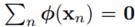，之后再看不是0均值的情况。这样，变换后样本的协方差阵就变为：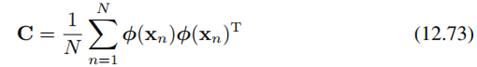

协方差阵的特征值分解变为：

现在的形式是phi(x_n)*phi(x_n)^T，我们想把它变为包含phi(x_n)^T*phi(x_n)的形式，以便利用核而不是直接用变换后的样本phi(x_n)来求解。
把刚才给出的(12.73)代入(12.74)，我们可以得到：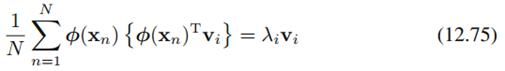

这说明v_i可以表示为phi(x_n)的线性组合：

但我们不知道这个系数a是什么，因为我们并不显式地知道非线性映射phi(x)。所以，这个a是我们之后要去求解的对象。
将12.76代回到12.75，可以得到：

两边都左乘phi(x_l)^T，核这个神秘角色就出现在我们面前了：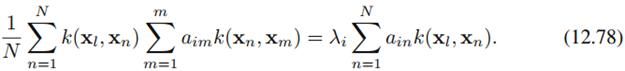

写成矩阵形式，就是：

两边都消去一个K（这样做不影响非0特征值）：

和传统PCA一样，有归一化约束：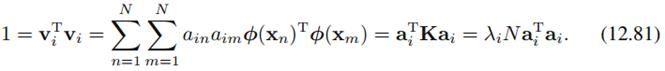

这样，这个问题同样变成了特征值分解问题，我们可以(12.80)和(12.81)求出a_i和lambda_i。我们经过变换的样本phi(x)再经过特征向量投影后的值，也就可以表示为：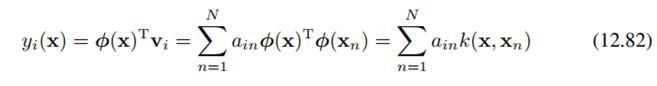

注意这里是用x和x_n的核的线性组合来表示的。由于主方向并不是线性的，所以我们无法求出它的形式是什么，而是只能求出如何通过核函数来得到投影到主方向后的降维形式如何用核函数表示出来。

我们先前为了简化计算而假定非线性映射phi(x_n)有0均值，现在去掉这个假设，将其扩展到一般形式。我们要减去均值以及计算减去均值之后的核矩阵：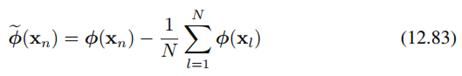 

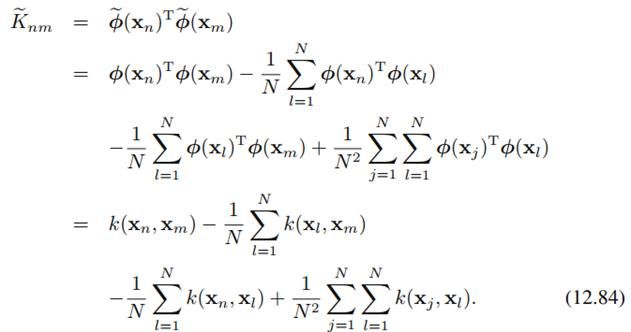
用K弯的矩阵形式：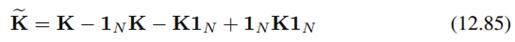

就可以像先前一样表示样本经过非线性变换在主方向下的投影。
KPCA有一个缺点，就是K是NxN维的，而传统PCA的样本协方差阵是DxD维的，那么在数据规模相对于特征维度来说很大时，计算效率就比较低。

这么顺着讲公式是有点枯燥。。可能还没上次讲点基本的东西比较有趣。特别是一些细节。大家自己也要多看看，PRML这种书真是每看一遍都有新发现。

 

我现在讲第12章最后的一小部分：12.4的非线性隐变量模型。
先来看看独立成分分析ICA。前面讲到，PCA假设隐变量服从高斯分布，这样想得到各维之间独立的隐变量，只需旋转隐变量使其协方差阵为对角阵即可，即隐变量各维之间线性无关。对于高斯分布来说，线性无关就是独立，因此其联合分布可分解为各维分布的乘积。
如果不要求隐变量一定是高斯分布，但仍保持观察变量和隐变量之间具有线性关系，那就是这一小节讲到ICA。这样的话，协方差阵为对角阵就不够了，因为对于任意分布来说，线性无关只是独立的必要条件而非充分条件。
得到这个独立解可以有很多方法，比如用高阶统计量而不仅仅是二阶的协方差来度量独立性，或者用互信息等方式来度量。书中介绍了一种描述隐变量的重尾分布：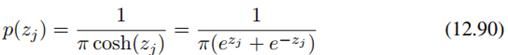

但也可以用其他分布。实际上这类分布可以分为超高斯和次高斯两种。具体细节可以看那本ICA的专著，可以在这里下载：http://ishare.iask.sina.com.cn/f/16979796.html
http://ufldl.stanford.edu/tutorial/index.php/ICA 和 http://ufldl.stanford.edu/tutorial/index.php/RICA 也有一些ICA的介绍，而且提供了一个不错的代码框架。我们如想实现那里介绍的方法，只需填入一小部分代码即可。

下面看一下autoassociative neural networks：
这一小节讲到的autoassociative neural networks，实际上就是最近deep learning中研究比较多的autoencoder。它的基本思想，就是让输入经过多层线性或非线性变换后，得到的输出尽量接近输入，然后取中间一层神经元作为隐变量。
最简单的两层情况是：

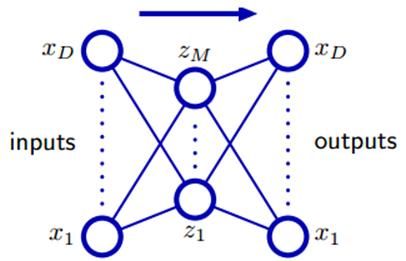
多层的话就是：

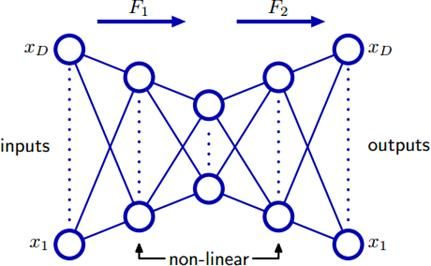
这里提到一点：中间隐变量的数量M需要小于输入变量的维度D。不过，现在deep learning中一般会对隐变量添加稀疏约束，这样就可以让M大于D且具有稀疏性，可以更好地描述数据。
本小节最后也提到，由于包含了非线性变换，因此目标函数不再是简单的二次函数，会变成非凸问题，优化起来容易陷入局部极值。deep learning解决的问题之一，就是利用逐层优化的pretraining方式，使得在最后整体优化之前，找到一个比较好的初始解，这样即使陷入局部极值，找到的也会是比较好的局部极值。优化方式和传统神经网络相似，也是反向传播（BP）算法。具体步骤可参见：http://ufldl.stanford.edu/tutorial/index.php/Autoencoders ，和ICA一样，也有一个不错的代码框架，实现起来非常简单。

最后看一下12.4.3的非线性流形思想。我们可用多种方法来构造非线性流形：
首先，我们可以用分段线性的方法，去捕捉非线性流形的信息。比如，可以先用kmeans等聚类算法，把数据分成多个聚类，然后在每个聚类上应用PCA等线性降维方法。
其次，我们可以参数化曲线，并像PCA那样找到合适的参数，以便用曲线形式表示数据的主成分：

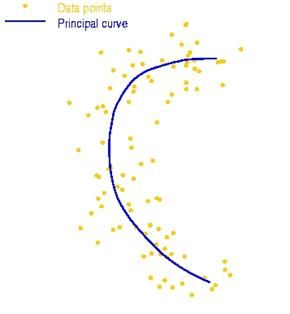
这种方法称作主曲线分析，后来也有主曲面分析等推广。可参见：http://www.iro.umontreal.ca/~kegl/research/pcurves/
最后看一下MDS、ISOMAP和LLE。MDS是从点对距离出发、希望降维后样本之间的点对距离能够尽量保持之前的点对距离。目标函数和求解方法都比较简单，这里就不赘述了。值得注意的是，这里我们并不需要每个样本的具体坐标，而是只需要知道样本之间的相对关系即可。而且，在欧氏距离下，MDS得到的坐标和PCA投影到最大主方向上的坐标是完全等价的。当然，MDS中使用的点对距离可以是任意的距离度量，因此得到的结果也可能和PCA投影坐标相去甚远。
ISOMAP和LLE是点燃流形学习这把大火的两篇论文，都发表在science上。ISOMAP利用了MDS，只不过使用的距离度量是测地线距离，也就是通过样本相连的最短距离。比如从A经过B、C到D，而且这条路径是最短的A与D之间的路径，那么这条最短路径的长度就是A与D之间的测地线距离。LLE的思想同样很简单：它用样本点x的局部邻域内的样本去线性表示x，然后希望映射到低维空间后，其局部线性关系尽量保持不变，也就是说，局部的线性表示系数和邻域样本都尽量保持不变。LLE具体可参见：http://www.cs.nyu.edu/~roweis/lle/ ，有很详细的算法介绍和写得非常漂亮的matlab代码。可惜作者sam roweis前几年不幸去世，是机器学习界的一大损失。
可以看到，前面介绍的以ISOMAP和LLE为代表的流形学习，其思想都是在低维空间中保持原先在高维空间中的某种样本之间的关系。这正是流形学习的核心思想：通过流形可能具有的先验信息，以保持样本中蕴含的关系为约束，来找到高维样本嵌入到低维流形的坐标。
后面还介绍了GTM和SOM两种方法，提到前者可看作后者的概率方法，但我并不太了解它们，所以这里就不多说了。谢谢大家。这章就是这样：）

 

==========================讨论==================================

快乐的孩纸(328509423) 22:05:41 
autoencoder 实际上就是intput x，output x，来学习隐层，然后用隐层去做预测y？

Wilbur_中博(1954123) 22:07:31 

是的，我做过一些实验，还挺好用的。有一些变种，比如对输入加一些噪声，但输出仍然是不带噪声的x，这样就是denoising autoencoder了。

快乐的孩纸(328509423) 22:08:47 
那如果是两层的autoencoder只有一个隐层，要是多个隐层呢？比如中间有3个隐层，得到这3个隐层，怎么用呢？这意味着intput x这个vector被表达成了，三个有层次的vectors了。
Wilbur_中博(1954123) 22:11:11 
不是，就用最中间的那个隐层。你可以看成输入经过多次映射到达中间那个隐层，然后又经过多次映射恢复回先前的输入到达输出。
快乐的孩纸(328509423) 22:12:09 
那就是autoencoder每次都是奇数层，然后得到中间的隐层，抽出来后用作regression来预测y？
你是谁？(271182928) 22:12:42 
对，就保留隐含层。没想到这样对x重新表达后，再用regression来预测y会效果很好。那隐含层的x'向量，一般就假设是相互独立了吧。也就是开始的x里的correlation被抹去了。
Wilbur_中博(1954123) 22:15:30 
对。比如说从100维输入到80维，再到60维，然后恢复的时候也是先到80维，再到100维。但其实我想有没有可能不必对称？比如从100到80到60，恢复的时候直接重构回100？我没有试过。我觉得可以试试。现在autoencoder的发展也蛮快的。但理论方面其实还差得很多，讲不出什么道理。效果确实还可以。

淘沙(271937125) 22:11:47 
能推荐 流形学习 的资料吗？

Wilbur_中博(1954123) 22:15:30 

流形学习的资料蛮多的。里面思想和分支也很多。dodo的这篇文章非常好：http://blog.sina.com.cn/s/blog_4d92192101008end.html
我觉得还是要抓流形学习的主要思想吧。而且流形学习比较好的一点就是，一般都会提供代码，我们可以从代码中学到很多。浙大的何晓飞和蔡登在这方面也很厉害，你可以去他们的主页看看。

初学者(75553395) 22:16:42 
弱问 这样的意思是之后的输入 只用隐含层就行了？

Wilbur_中博(1954123) 22:17:50 

对，新来样本也用那个神经网络的权值映射到隐含层，然后用隐含层的输出作为分类器等传统方法的输入。
不过其实还有各种技巧吧。。需要有监督的fine-tuning之类的。
快乐的孩纸(328509423) 22:19:49 
autoencoder我不熟悉，我还有一个问题。 现在感觉和pca挺像的，就是learning的过程中只依赖原始intput：x，利用x内部的correlation和interaction来重新表达隐含层。 但是从直觉上看，在learning过程中，不仅考虑x的correlation，以及x与y的correlation，来最后得到x的新表达，理论上更利于y的预测精确度。比如PLS. 
Wilbur_中博(1954123) 22:24:35 

你说的对。其实要考虑的东西有很多，比如x本身的结构，x和y的关系，如果有多任务的话那么y也是矩阵形式的，也可以研究y之间的结构和关系。还有我们从x提取出来的特征，特征之间其实也还有关系，因为提取特征也只是某一方面的假定而已。现在很火的CNN，如果在特征之间做一些工作，效果肯定还能更好。所以机器学习要研究的问题可以说无穷无尽。

快乐的孩纸(328509423) 22:26:03 
如果是多任务的话，那是multitask learning了。多个y之间也有correlation。 Jieping Ye那个组经常搞这个
XXX<[email protected]> 22:26:04 
@Wilbur 流型学习，近两年哪些方面比较火？
Wilbur_中博(1954123) 22:26:21 
@快乐的孩纸 没错
XXX<[email protected]> 22:26:27 
Jieping Ye都快把multitask learning玩坏了
快乐的孩纸(328509423) 22:26:42 
那公式推的一把一把的。@Wilbur 有没有autoencoder的好的源码framework啊？给我一个链接，我能try一下么？
Wilbur_中博(1954123) 22:27:55 
@XXX 流形学习这两年基本沉寂了，火的时候已经过去了。不过还是非常实用的。
XXX<[email protected]> 22:30:04 
问一个肤浅的问题，现在火啥？（除了Deep learning）@Wilbur 
Wilbur_中博(1954123) 22:30:51 
@快乐的孩纸 你可以照着http://deeplearning.stanford.edu/wiki/index.php/Exercise:Sparse_Autoencoder 实现一下
@XXX 我觉得hashing trick也挺火的，值得关注。另外组合优化相关的近似算法和快速算法也可以关注关注。
XXX<[email protected]> 22:33:04 
hashing trick 是指 learning to hash？组合优化相关的近似算法？这个哪里有？
Wilbur_中博(1954123) 22:35:23 
倒不一定是learning to hash。简单的hash code也可以有不错的效果。比如google搞的WTA hashing和今年CVPR的best paper就是不错的hashing trick的文章。我个人不是太喜欢learning to hash。。所有以前有的连续情况的算法都搞成二元约束算法，有点恶心。
组合优化方面的比如submodular optimization了，还有：
Towards Efficient and Exact MAP-Inference for Large Scale Discrete Computer Vision Problems via Combinatorial Optimization
我觉得做CV的人也值得关注。还有挺多的。。这是个大方向。
XXX<[email protected]> 22:39:33 
那 快速算法 又是指？难道是搞个收敛速率高的算法，再证个bound？
Wilbur_中博(1954123) 22:45:26 
嗯，组合优化的技巧很多。。松弛到较大的解集、限制到较小的解集，看起来背道而驰但还都能用，就是分析起来思路不太一样。还有其他各种各样的思路。不过我其实也不是特别了解，就不妄谈了。。但机器学习或计算机视觉里的组合优化，肯定还是会有很大发展空间的。

 

PRML读书会讲稿PDF版本以及更多资源下载地址：http://vdisk.weibo.com/u/1841149974