【OpenCV】学习OpenCV3——常见的图像变换（1）

  我们遇到的简单的图像变换是调整图像的大小，使其变大或变小。这些操作比你想象的稍微复杂，因为调整也带来了像素如何差值（放大）或合并（减少）的问题。

一、 均匀调整cv2.resize

  我们经常会遇到一些尺寸的图像，我们想转换成其他尺寸，可能想要增大或缩小图像，这两个操作都可以通过相同的函数实现。
  dst=cv2.resize(src, dsize, fx=None, fy=None, interpolation=None)

参数	含义
src	输入图像
dsize	输出图像的大小：1）绝对尺寸，直接将dsize设置成想要输出的大小；2）相对尺寸，直接将值设为（0,0），并对fx,fy进行赋值
fx=None	沿水平轴的比例因子，既x轴缩放系数
fy=None	沿垂直轴的比例因子，既y轴缩放系数
interpolation=None	差值方法，默认为双线性差值。

interpolation差值选项	含义
cv2.INTER_NEAREST	最近邻差值
cv2.INTER_LINEAR	双线性差值
cv2.INTER_AREA	像素区域重采样
cv2.INTER_CUBIC	双三次差值
cv2.INTER_LANCZOS4	差值超过8*8个邻域

#调整图像大小
resize_img=cv2.resize(img,(750,750))#原图，想要调整的大小

二、 图像金字塔

  图像金字塔是图像的集合，它由单个原始图像产生。常用的两种金字塔：高斯金字塔和拉普拉斯金字塔。

2.1 高斯金字塔

2.1.1 下采样cv2.pyrDown（）

  高斯金字塔用于降采样图像。
  原理：将层Gi与高斯核卷积，然后去除每个偶数行和列，从而生成高斯金字塔的Gi+1层。在输入图像G0上不断迭代上述过程产生整个金字塔。
  dst=cv2.pyrDown(src, dstsize=None, borderType=None)

参数	含义
src	输入图像
dstsize=None	输出图像的尺寸，默认条件下输出图像的大小为((src.shape[0]+1)/2,(src.shape[1]+1)/2)，既是原图像的1/4.dstsize可以指明输出图像的大小，但必须遵循严格的限制。
borderType=None	边界填充的类型

dst=cv.pyrDown(temp)

2.1.2 高斯金字塔

  原理：有一张图像，希望构建一系列新图像，每个都从其前身缩减。。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
''''''
def pyramid_demo(image):
    level=3#定义金字塔层数
    temp=image.copy()
    pyramid_images=[]
    for i in range(level):
        dst=cv.pyrDown(temp)#降采样
        pyramid_images.append(dst)
        cv.imshow('pyramid_down_'+str(i+1),dst)
        temp=dst.copy()
    return pyramid_images
img=cv.imread(r'D:\Project\Opencv\Learning01\angelababy.jpg')
cv.imshow('origin',img)
pyramid_demo(img)
cv.waitKey(0)

2.2 拉普拉斯金字塔

2.2.1 上采样cv2.pyrUp（）

  原理：将现有图像转换为每个方向两倍大的图像。
  dst=cv2.pyrUp(src, dstsize=None, borderType=None)

参数	含义
src	输入图像
dstsize=None	输出图像的尺寸，默认条件下输出图像的大小为src的两倍大小相同。dstsize可以指明输出图像的大小，但必须遵循严格的限制。
borderType=None	边界填充的类型

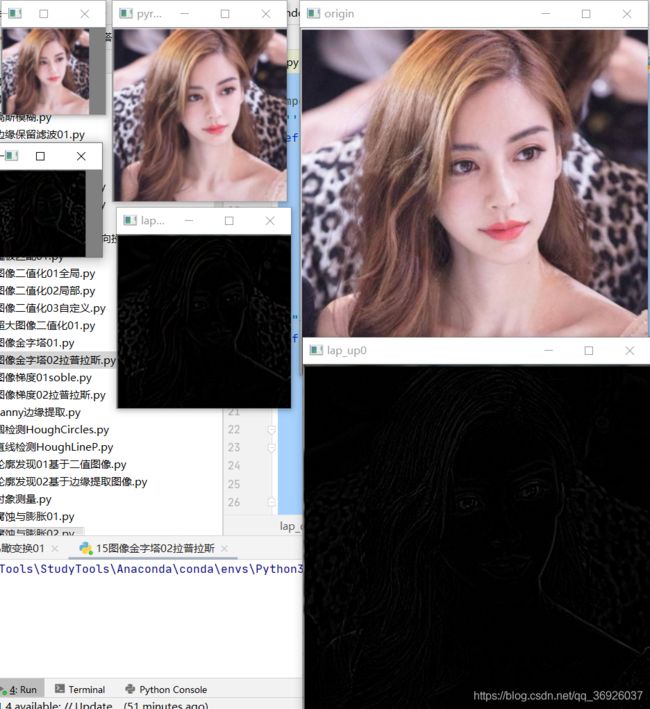
2.2.2 拉普拉斯金字塔

  可以观察到，上采样并不是下采样的逆，因为下采样是丢失信息的操作，为了恢复原始图像，需要访问高斯金字塔下采样过程中丢失的信息，这个数据形成拉普拉斯金字塔。。
通过高斯金字塔可以得到拉普拉斯金字塔。Ln=gn-expand(gn-1)

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
'''高斯金字塔'''
def pyramid_demo(image):
    level=3#定义金字塔层数
    temp=image.copy()
    pyramid_images=[]
    for i in range(level):
        dst=cv.pyrDown(temp)
        pyramid_images.append(dst)
        cv.imshow('pyramid_down_'+str(i+1),dst)
        temp=dst.copy()
    return pyramid_images#没有原图
"""拉普拉斯金字塔"""
def lap_demo(image):
    '''拿到高斯金字塔'''
    pyramid_images=pyramid_demo(image)#得到高斯金字塔
    level=len(pyramid_images)

    for i in range(level-1,-1,-1):#从最小的高斯金字塔开始，到最大的金字塔（没有包含原图）
        if (i-1)<0:#原图
            expand=cv.pyrUp(pyramid_images[i],dstsize=image.shape[:2])
            lpls=cv.subtract(image,expand)
            cv.imshow('lap_up'+str(i),lpls)
        else:
            expand = cv.pyrUp(pyramid_images[i], dstsize=pyramid_images[i-1].shape[:2])
            lpls = cv.subtract(pyramid_images[i-1], expand)  # 得到拉普拉斯金字塔
            cv.imshow('lap_up'+str(i), lpls)

img=cv.imread(r'D:\Project\Opencv\Learning01\fang.png')
cv.imshow('origin',img)
lap_demo(img)
cv.waitKey(0)

三、不均匀映射

  本节是图像的几何操作，这些操作包括均匀调整大小（详见1.1节）和不均匀调整大小（扭曲）。
  几何变换：拉伸、扭曲、收缩、旋转图像。对于平面区域有两种几何变换：
  （1）仿射变换：使用2×3矩阵的变换。
  （2）透视变换：使用3×3矩阵的变换
参考1：https://zhuanlan.zhihu.com/p/36082864
参考2：https://blog.csdn.net/aliyanah_/article/details/85726042
参考3：https://blog.csdn.net/lz867422770/article/details/92799619

3.1 仿射变换

3.1.1 概念

  定义：
  仿射变换，又称仿射映射，是指在集合中，图像从一个向量空间进行一次线性变换和一次平移变换，变换到另一个向量空间的过程。
  特征：
  （1）仿射变换可以叫做【平面变换】或【二维坐标变换】。
  （2）仿射变换保证二维图形的“平直性”和“平行性”。平直性：变换前是直线的，变换后也是直线；平行性：二维形状之间的相对位置关系保持不变。可以将任意矩形转换为平行四边形，可以挤压形状，但是都必须保持两边平行。
  公式：


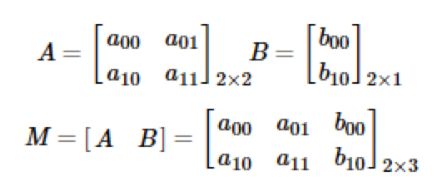
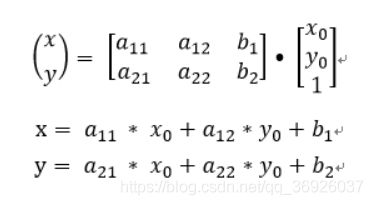
  M：表示变换矩阵，包括线性变换矩阵A和平移矩阵B。
  [x0,y0]：代表原始图像矩阵，是一个二维数组，x代表像素的横坐标，y代表像素的纵坐标。
  (x,y)：代表经过过仿射变换后的图像矩阵。
  仿射变换的方程组有6个未知数，所以求解变换矩阵就要求3组映射点，三个点刚好确定一个平面。在应用层面，放射变换是图像基于3个固定顶点的变换。
  （1）仿射变换进行图像平移：如果线性变换矩阵A=[[1, 0], [0,1]]，那么A点乘矩阵[x, y]T 就不会改变[x, y]T的信息，此时，仿射变换就变成了平移操作，移动的行列值就是矩阵B中的元素值；
  （2）仿射变换进行图像旋转：如果线性矩阵A=[[cosθ, -sinθ], [sinθ, cosθ]]，那么线性变换就变成了图片的旋转操作，旋转角度θ。矩阵B代表旋转中心的坐标便宜量

3.1.2 应用

  获得转换矩阵M=cv2.getAffineTransform(src, dst)。src和dst是3个点的数组在getAffineTransform中定义了两个平行四边形，src中的点通过应用warpAffine，使用转换矩阵M映射到dst中的对应点，所有其他点都将随之拖曳，一旦这三个独立的角点被映射，所有其他点的映射可以被完全确定。

参数	含义
src	源图像中3点坐标
dst	目标图像中3点坐标。

  仿射变换：dst=cv2.warpAffine(src, M, dsize, flags=None, borderMode=None, borderValue=None)

参数	含义
src	源图像中四边形顶点的坐标
M	转换矩阵
dsize	输出图像的大小，类型与src相同
flags=None	差值方法，同cv2.resize的差值选项相同
borderMode=None	边界填充方法
borderValue=None	如果使用cv2.BORDER_CONSTANT则使用该值进行填充

import cv2
import numpy as np

img=cv2.imread(r'D:\Project\Opencv\Learning02\image022.png')
cv2.imshow('oringin image',img)

#定义3个点
width,height=250,350
pts1=np.float32([[98,189],[252,161],[135,419]])
pts2=np.float32([[0,0],[width,0],[0,height]])

#转换矩阵
matrix=cv2.getAffineTransform(pts1,pts2)

#转换后的图像
img_output=cv2.warpAffine(img,matrix,(width,height))
cv2.imshow("warp image",img_output)
#
cv2.waitKey(0)#0代表无限延迟，数值代表延迟多少毫秒
#
cv2.warpAffine()

3.2 透视变换

3.2.1 概念

  定义：
  透视变换就是将图片投影到一个新的视平面，也称为投影映射。
  特征：
  （1）透视变换可以叫做【空间变换】或【三维坐标变换】。
  （2）透视变换改变了直线之间的平行关系。可以将矩形转换为任意四边形，不用保持物体形状的平直性。
  公式：

  M：表示变换矩阵，包括线性变换矩阵A和平移矩阵B，仿射变换可以看作透视变换的一种特殊形式。
  [x0,y0]：代表原始图像矩阵，是一个二维数组，x代表像素的横坐标，y代表像素的纵坐标。
  (x’,y’)：代表经过过仿射变换后的图像矩阵。
  透视变换的方程组有8个未知数，所以求解变换矩阵就需要4组映射点，并且要保证至少三个不在一条直线上。四个点刚好确定一个三维空间。在应用层面，透视变换是图像基于4个固定顶点的变换。已知4个点的坐标和想要变换成的矩阵坐标，即可求出3*3的变换矩阵

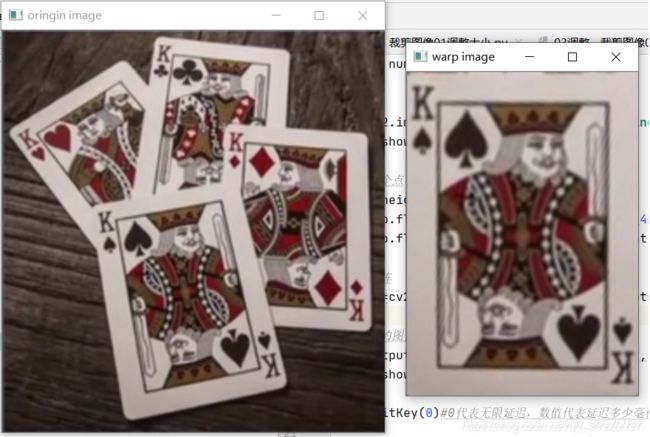
3.2.2 应用

  获得转换矩阵：M=cv2.getPerspectiveTransform(src, dst)src和dst是4个点的数组。

参数	含义
src	源图像中四边形顶点的坐标
dst	目标图像中相应四边形顶点的坐标。

  透视变换：dst=cv2.warpPerspective(src, M, dsize, flags=None, borderMode=None, borderValue=None)

参数	含义
src	源图像中四边形顶点的坐标
M	转换矩阵
dsize	输出图像的大小，类型与src相同
flags=None	差值方法，同cv2.resize的差值选项相同
borderMode=None	边界填充方法
borderValue=None	如果使用cv2.BORDER_CONSTANT则使用该值进行填充

import cv2
import numpy as np

img=cv2.imread(r'D:\Project\Opencv\Learning02\image02.png')
cv2.imshow('oringin image',img)
#定义四个点
width,height=250,350
pts1=np.float32([[98,189],[252,161],[135,419],[307,381]])
pts2=np.float32([[0,0],[width,0],[0,height],[width,height]])
#获得透视变换的转换矩阵
matrix=cv2.getPerspectiveTransform(pts1,pts2)
#转换后的图像
img_output=cv2.warpPerspective(img,matrix,(width,height))#参数：输入图像，3*3变换矩阵,输出图像的大小
cv2.imshow("warp image",img_output)
cv2.waitKey(0)#0代表无限延迟，数值代表延迟多少毫秒