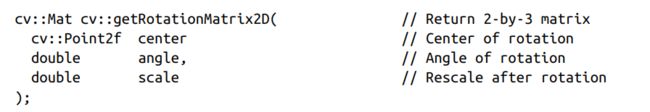OpenCV笔记13——图像的几何变换（旋转，平移，缩放，仿射，透射）

1.相关API

通过下面的API就可以进行一般的平移，旋转，缩放，仿射等操作；
图像变形扭曲:

---

2.平移变换

2.1原理

下面是二维图像一般情况下的变换矩阵（旋转+平移），当我们只需要平移的时候，取Theta的值为0，a和b的值就代表了图像沿x轴和y轴移动的距离；

进一步简化：

将上式展开：

---

2.2实验代码

    Mat src = imread("E:/image/girl2.jpg");
    Mat mov_mat = (Mat_<double>(2, 3) << 1, 0, 20, 0, 1, 50);//沿x轴移动20沿y轴移动50
	Mat src_mov;
	warpAffine(src, src_mov, mov_mat, src.size());
	imshow("Move", src_mov);

2.3运行结果

3.旋转变换

同平移一样，此时的移动参数a,b设为0，即不对图像进行平移操作，指定旋转角度就OK；

3.1实验代码

	
	Mat src = imread("E:/image/girl2.jpg");
	Mat rota_mat = (Mat_<double>(2, 3) << 0.707, -0.707, 0, 0.707, 0.707, 0);
	Mat src_rota;
	warpAffine(src, src_rota, rota_mat, src.size());

3.2运行结果

如果要显示出完整的图像，只需要把目标图像再设置的大一点即可；

---

旋转变换矩阵获取：

在OpenCV中可以定义一个旋转矩阵来进行旋转以及缩放操作，比上面这种更加的方便，实验代码如下：

	Point center = Point(warp_dst.cols / 2, warp_dst.rows / 2);//定义旋转中心点
	double angle = 45;//定义旋转角度，逆时针为正旋转方向
	double scale = 0.6;//缩放比例
	Mat rot_mat = getRotationMatrix2D(center, angle, scale);//获取2*3转换矩阵
	Mat warp_rotate_dst;
	warpAffine(src, warp_rotate_dst, rot_mat, warp_dst.size());

运行结果：

---

4.仿射变换

4.1原理简介

如下图，三点确定一个平面，仿射变换的原理就是在原图像上确定三个点，然后对应到目标图像上的这三个点之间有一个变换关系，这个变换关系可以用一个2*3的矩阵来表示；

同样的，一个像素点的对应关系可以列出一个方程，如果想要求解变换矩阵中的六个参数的话，则至少需要六个方程，即需要三个像素点的对应关系；

仿射变换矩阵获取：

4.2实验代码：

    Mat src = imread("E:/image/girl2.jpg");
	if (src.empty())printf("Load Image Error");

    //定义三个初始点
	Point2f srcTri[3];
	srcTri[0] = Point2f(0.f, 0.f);
	srcTri[1] = Point2f(src.cols - 1.f, 0.f);
	srcTri[2] = Point2f(0.f, src.rows - 1.f);
	
    for (int i = 0; i < 4; i++)circle(src, srcTri[i], 15, Scalar(255, 0, 0), -1);//将选取的试验点标注出来

    //定义仿射后的三个点，根据你想要的变换效果
	Point2f dstTri[3];
	dstTri[0] = Point2f(src.cols*0.5f, 0.f);
	dstTri[1] = Point2f(src.cols - 1.f, 0.f);
	dstTri[2] = Point2f(0.f, src.rows - 1.f);

	Mat warp_mat = getAffineTransform(srcTri, dstTri);//获取2*3转换矩阵
	Mat warp_dst;
	warpAffine(src, warp_dst, warp_mat, warp_dst.size());//仿射变换

	imshow("Source image", src);
	imshow("Warp", warp_dst);

4.3运行结果

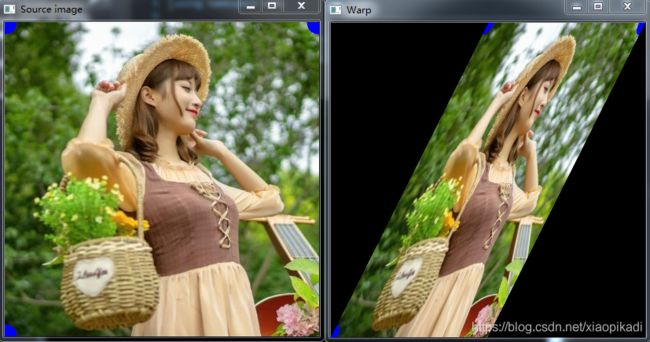
其实在正常的使用当中是反过来的，我们一般是通过这些变换将一些扭曲的图像进行还原修正，操作步骤类似；

所以我随便弄了一张扭曲的图片试了哈，效果如下：

---

5.透射变换

5.1透射变换的API

获取透射变换的矩阵：

透射变换在这里需要四个对应的像素点坐标；

透射变换：

5.2实验代码

    Mat src = imread("E:/image/chepai7.jpg");
	if (src.empty())printf("Load Image Error");
	
	Point2f src_PerPoint[4];//定义原图像中4个初始点坐标
	src_PerPoint[0] = Point2f(20, 200);
	src_PerPoint[1] = Point2f(215, 350);
	src_PerPoint[2] = Point2f(355, 10);
	src_PerPoint[3] = Point2f(550, 90);
	for (int i = 0; i < 4; i++)circle(src, src_PerPoint[i], 15, Scalar(255, 0, 0), -1);//将选取的试验点标注出来

	Point2f dst_PerPoint[3];//定义透射后的4个像素点坐标
	dst_PerPoint[0] = Point2f(10, 20);
	dst_PerPoint[1] = Point2f(0, 300);
	dst_PerPoint[2] = Point2f(450, 10);
	dst_PerPoint[3] = Point2f(450, 300);

	Mat per_src;
	Mat per_mat = getPerspectiveTransform(src_PerPoint, dst_PerPoint);//获取透射变换矩阵
	warpPerspective(src, per_src, per_mat, src.size());//透射变换
		
	imshow("Source image", src);
	imshow("per_src", per_src);

5.3运行结果

看到透射的效果后相信你应该对仿射和透射的操作会有更直观的认识了吧；

参考文章链接：
1.https://zhuanlan.zhihu.com/p/36082864
2.https://docs.opencv.org/master/d4/d61/tutorial_warp_affine.html