基于改进鲸鱼优化算法的WSN覆盖优化
文章目录
- 一、理论基础
-
- 1、WSN节点覆盖模型
- 2、基本鲸鱼算法
- 3、改进鲸鱼优化算法
-
- (1)量子位Bloch球面初始化
- (2)改进搜索猎物过程
- (3)莱维飞行扰动策略
- 二、算法流程
- 三、仿真实验与分析
-
- 1、实验环境
- 2、实验结果
-
- (1)与FA算法对比
- (2)与EABC算法对比
- 四、参考文献
- 五、Matlab代码
一、理论基础
1、WSN节点覆盖模型
假设WSN监测区域是个二维平面,且数字化为 L × M L×M L×M的网格,每个网格大小设为1。在该区域部署 N N N个同构传感器,节点集合可以表示为 Z = { z 1 , z 2 , ⋯ , z N } Z=\{z_1,z_2,\cdots,z_N\} Z={ z1,z2,⋯,zN},都具有相同的感知半径 R s R_s Rs和通信半径 R c R_c Rc, R s ≤ 2 R c R_s≤2R_c Rs≤2Rc。文采用布尔模型(0/1模型)作为节点感知模型,只要目标处于节点感知范围内,即可成功的被感知。假设在被监测区域的某个节点 z i z_i zi的坐标为 ( x i , y i ) (x_i,y_i) (xi,yi),目标点的位置 T j T_j Tj坐标为 ( x j , y j ) (x_j,y_j) (xj,yj),则节点与目标点的距离为: d ( z i , T j ) = ( x i − x j ) 2 + ( y i − y j ) 2 (1) d(z_i,T_j)=\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}\tag{1} d(zi,Tj)=(xi−xj)2+(yi−yj)2(1)用 p ( z i , T j ) p(z_i,T_j) p(zi,Tj)表示节点 z i z_i zi对 T j T_j Tj的感知质量,当 T j T_j Tj的位置在节点 z i z_i zi的感知范围内时,则感知质量为1;否则节点 z i z_i zi对 T j T_j Tj的感知质量为0,数学表达式为: p ( z i , T j ) = { 1 i f d ( z i , T j ) ≤ R s 0 o t h e r w i s e (2) p(z_i,T_j)=\begin{dcases}1\quad if\, d(z_i,T_j)≤R_s\\0\quad otherwise\end{dcases}\tag{2} p(zi,Tj)={ 1ifd(zi,Tj)≤Rs0otherwise(2)通常,传感器对目标的感知概率小于1,为了提高对目标的感知概率,需要多个传感器协同探测,则WSN对某一目标的感知概率为: p ( Z , T j ) = 1 − ∏ i = 1 N [ 1 − p ( z i , T j ) ] (3) p(Z,T_j)=1-\prod_{i=1}^N[1-p(z_i,T_j)]\tag{3} p(Z,Tj)=1−i=1∏N[1−p(zi,Tj)](3)该监测区的覆盖率是所有传感器节点覆盖的目标点数与该区域总的目标点数的比值,定义为: R c o v = ∑ j = 1 L × M p ( Z , T j ) L × M (4) R_{cov}=\frac{\displaystyle\sum_{j=1}^{L×M}p(Z,T_j)}{L×M}\tag{4} Rcov=L×Mj=1∑L×Mp(Z,Tj)(4)将式(4)作为目标函数,用改进的鲸鱼算法求得 R c o v R_{cov} Rcov的最优值以提高WSN的覆盖质量。
2、基本鲸鱼算法
请参考这里。
3、改进鲸鱼优化算法
(1)量子位Bloch球面初始化
将量子位的3个坐标看作3个并列的解,即每个鲸鱼个体包含对应优化问题的三个解,分别为 x x x解、 y y y解和 z z z解: { p i , x = ( c o s φ i 1 s i n θ i 1 , ⋯ , c o s φ i n s i n θ i n ) p i , y = ( s i n φ i 1 s i n θ i 1 , ⋯ , s i n φ i n s i n θ i n ) p i , z = ( c o s θ i 1 , ⋯ , c o s θ i n ) (5) \begin{dcases}p_{i,x}=(cos\varphi_{i1}sin\theta_{i1},\cdots,cos\varphi_{in}sin\theta_{in})\\p_{i,y}=(sin\varphi_{i1}sin\theta_{i1},\cdots,sin\varphi_{in}sin\theta_{in})\\p_{i,z}=(cos\theta_{i1},\cdots,cos\theta_{in})\end{dcases}\tag{5} ⎩⎪⎨⎪⎧pi,x=(cosφi1sinθi1,⋯,cosφinsinθin)pi,y=(sinφi1sinθi1,⋯,sinφinsinθin)pi,z=(cosθi1,⋯,cosθin)(5)在IWOA中,1个量子位包含3个Bloch坐标,每个坐标对应一个优化解。由于Bloch坐标下每一维的范围是 [ − 1 , 1 ] [-1,1] [−1,1],为解决连续优化问题,需要进行解空间变化,即将每个鲸鱼对应的三个Bloch坐标由单位空间映射到优化问题解空间。记鲸鱼 P i P_i Pi上第 j j j个量子位的Bloch坐标为 [ x i j , y i j , z i j ] T [x_{ij},y_{ij},z_{ij}]^T [xij,yij,zij]T,则对应解空间变量为: { X i x j = 0.5 [ b j ( 1 + x i j ) + a j ( 1 − x i j ) ] X i y j = 0.5 [ b j ( 1 + y i j ) + a j ( 1 − y i j ) ] X i z j = 0.5 [ b j ( 1 + z i j ) + a j ( 1 − z i j ) ] (6) \begin{dcases}X_{ix}^j=0.5[b_j(1+x_{ij})+a_j(1-x_{ij})]\\X_{iy}^j=0.5[b_j(1+y_{ij})+a_j(1-y_{ij})]\\X_{iz}^j=0.5[b_j(1+z_{ij})+a_j(1-z_{ij})]\end{dcases}\tag{6} ⎩⎪⎨⎪⎧Xixj=0.5[bj(1+xij)+aj(1−xij)]Xiyj=0.5[bj(1+yij)+aj(1−yij)]Xizj=0.5[bj(1+zij)+aj(1−zij)](6)式中, i = 1 , 2 , ⋯ , m , j = 1 , 2 , ⋯ , n i=1,2,\cdots,m,j=1,2,\cdots,n i=1,2,⋯,m,j=1,2,⋯,n, [ a j , b j ] [a_j,b_j] [aj,bj]为第 j j j个量子位的取值范围。
每个鲸鱼对应Bloch坐标中的3个可行解,这种初始化方式能改善初始鲸鱼群的多样性,进而改善初始种群的质量,提高算法的全局优化能力。
(2)改进搜索猎物过程
本文引入了一个新的参数 U U U,它将自适应地改变步长,平衡全局搜索和局部搜索能力,将其应用于位置更新公式中, U U U的公式为: U = e 10 k (7) U=e^{10k}\tag{7} U=e10k(7) k = ( r a n d − 0.5 ) ( 1 − t / M a x i t e r ) (8) k=(rand-0.5)(1-t/Max_{iter})\tag{8} k=(rand−0.5)(1−t/Maxiter)(8)式中, r a n d rand rand为 [ 0 , 1 ] [0,1] [0,1]之间的随机数, t t t为当前迭代次数, M a x i t e r Max_{iter} Maxiter为最大迭代次数。新的位置更新公式为: D ′ = ∣ X r ( t ) − X ( t ) ∣ (9) D'=|\boldsymbol X_r(t)-\boldsymbol X(t)|\tag{9} D′=∣Xr(t)−X(t)∣(9) X ( t + 1 ) = X ( t ) − U s i g n ( a ) D ′ (10) \boldsymbol X(t+1)=\boldsymbol X(t)-Usign(a)D'\tag{10} X(t+1)=X(t)−Usign(a)D′(10)式中, s i g n ( ⋅ ) sign(\cdot) sign(⋅)为符号函数,取值为 − 1 , 0 , 1 -1,0,1 −1,0,1。
随着迭代次数的增加, U U U整体呈减小趋势。但是与原始WOA中的 A A A相比较, U U U既有较大步长,又有小步长,可以帮助IWOA较好地协调其探索和开发能力并在整个搜索过程中保持多样性。
(3)莱维飞行扰动策略
本文引入莱维飞行机制,对寻优过程中位置更新方式进行扰动操作, 改善算法易陷入局部最优及出现早熟收敛现象。通过莱维飞行,新的位置更新公式如下: X l ( t ) = X ( t ) + α ⊕ L e v y ( λ ) (11) \boldsymbol X^l(t)=\boldsymbol X(t)+\alpha ⊕Levy(\lambda)\tag{11} Xl(t)=X(t)+α⊕Levy(λ)(11)式中, X l ( t ) \boldsymbol X^l(t) Xl(t)为莱维飞行扰动后的位置, ⊕ ⊕ ⊕为点乘, α \alpha α为步长控制因子, L e v y ( λ ) Levy(\lambda) Levy(λ)表示随机搜索路径。具体的莱维飞行公式请参考这里。
由于不能保证莱维飞行扰动后的位置优于原位置,所以本文采用贪婪选择决定是否更新鲸鱼位置,即新位置适应度值优于原位置的适应度值则保留,否则舍弃,公式为: X ( t + 1 ) = { X l ( t ) f [ X l ( t ) ] < f [ X ( t ) ] X ( t ) f [ X l ( t ) ] ≥ f [ X ( t ) ] (12) \boldsymbol X(t+1)=\begin{dcases}\boldsymbol X^l(t)\quad f[\boldsymbol X^l(t)]
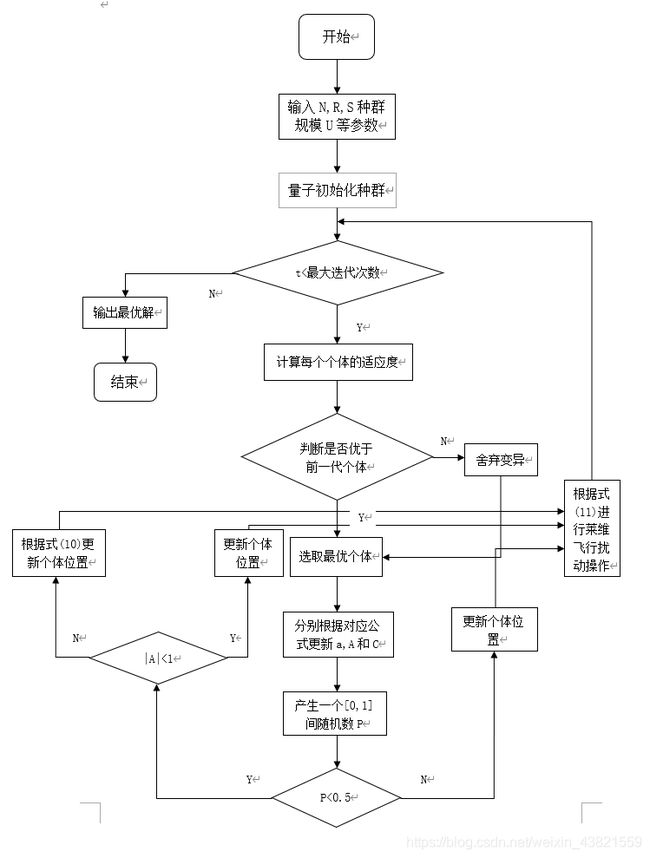
二、算法流程
三、仿真实验与分析
1、实验环境
为验证本文改进的鲸鱼算法应用于WSN覆盖优化性能,用MATLAB进行仿真,将原始WOA、改进后的IWOA 和其他文献的覆盖效果进行对比,其中实验的参数与其他文献的对应参数设置相同。参与对比的算法如表1所示。
2、实验结果
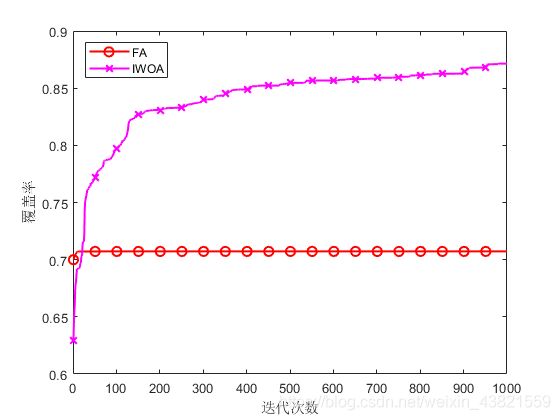
(1)与FA算法对比
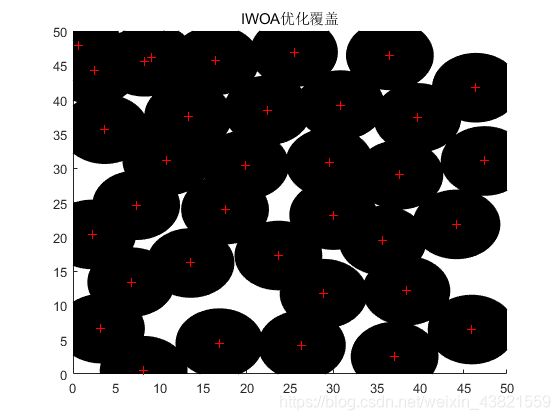
将实验参数设置与文献[2]相同, 设监测区域为 50 m × 50 m 50 m×50 m 50m×50m的二维平面, 传感器节点个数 N = 35 N=35 N=35,其感知半径是 R s = 5 m R_s = 5 m Rs=5m,通信半径 R c = 10 m R_c= 10 m Rc=10m,迭代1000次。初始部署、FA优化覆盖、IWOA优化覆盖如图2~4所示。

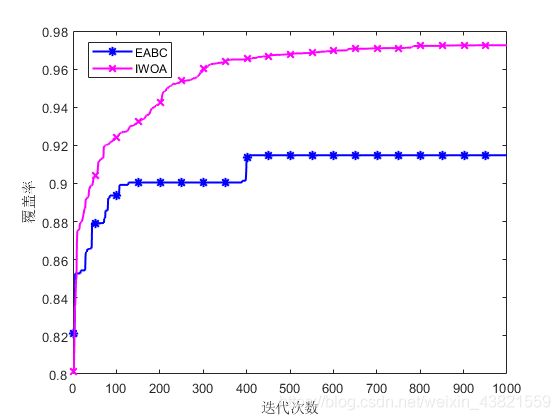
(2)与EABC算法对比
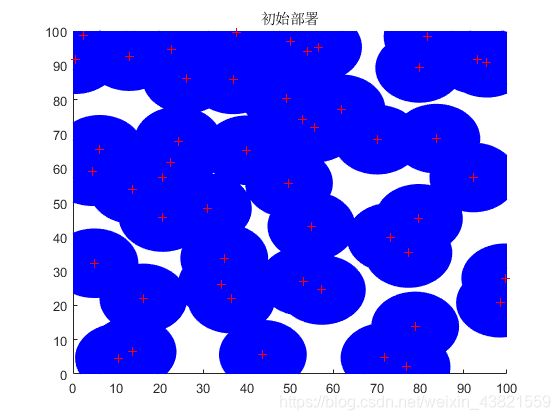
将实验参数设置与文献[3]相同,即监测区域为 100 m × 100 m 100 m×100 m 100m×100m的二维正方形平面,部署同构传感器节点个数 N = 50 N=50 N=50,其感知半径是 R s = 10 m R_s=10 m Rs=10m,通信半径 R c = 20 m R_c=20 m Rc=20m,迭代次数为1000。图6为EABC初始部署,图7为EABC优化覆盖图,图8为IWOA优化覆盖图,图9为二者对比图。
四、参考文献
[1] 宋婷婷, 张达敏, 王依柔,等. 基于改进鲸鱼优化算法的WSN覆盖优化[J]. 传感技术学报, 2020, 033(003):415-422.
[2] Tuba E , Tuba M , Beko M . Mobile wireless sensor networks coverage maximization by firefly algorithm[C]// Radioelektronika. IEEE, 2017:1-5.
[3] 于文杰, 李迅波, 羊行,等. 外推人工蜂群算法在WSN部署优化中的应用研究[J]. 仪表技术与传感器, 2017(6).
[4] ~心升明月~. 基于鲸鱼优化算法的函数寻优算法. CSDN博客.
[5] ~心升明月~. 基于嵌入莱维飞行的灰狼优化(LGWO)算法的函数寻优算法. CSDN博客.
五、Matlab代码
下载地址:
https://download.csdn.net/download/weixin_43821559/16605072