SLAM练习题（十二）—— ICP（Iterative Closest Point）

SLAM 学习笔记

ICP全称Iterative Closest Point，翻译过来就是迭代最近点。ICP在点云配准领域应用的非常广泛，因此基于深度相机、激光雷达的算法使用ICP的频率比较高。

推导ICP

以下题目来自计算机视觉life从零开始一起学习SLAM系列

推导ICP中的一个步骤
证明：《视觉SLAM十四讲》第174页公式7.55中的

各符号定义见书上，其中，tr表示矩阵的迹。

直接设出$q_i,R,q_i^{\prime }$:

高童靴收集的第二种答案看的不是很懂，暂时就先用这种简单粗暴的方式吧。

求解ICP原理

线性方法（SVD分解）

参考14讲173页。


最优性的证明可以参考之前的一篇文章：从零手写VIO(六)
通过对Ｗ进行奇异值分解，因为Ｒ满秩，所以Ｒ＝ＵＶ^T。

非线性方法

构建无约束优化问题

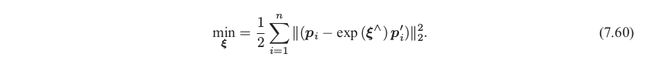
然后就是使用g2o进行优化了，g2o里面没有3D-3D的边，需要自己构建，自己算算误差对位姿扰动量的偏导数，参考书上175。

ICP实战

以下题目来自计算机视觉life从零开始一起学习SLAM系列

题目: 给定一个轨迹1,数据格式:timestamp tx ty tz qx qy qz qw, 自定义一个任意的旋转矩阵和平移向量(可
以尝试不同的值,甚至加一些噪声看看结果有什么变化),对轨迹1进行变换,得到一个新的轨迹2, 使用ICP算法
(提示:取平移作为三维空间点)估计轨迹1,2之间的位姿,然后将该位姿作用在轨迹2。

验证:ICP算法估计的旋转矩阵和平移向量是否准确;轨迹1,2是否重合。 如下是加了一个旋转平移量后的两个轨迹,经过ICP计算好位姿后再反作用在变换后的轨迹,最终两个轨迹是重合滴!

代码框架及数据 链接:https://pan.baidu.com/s/1a_6FGAd955EPED-duUqpPw 提取码:30sz

代码

/****************************
 * 题目：给定一个轨迹１，数据格式：timestamp tx ty tz qx qy qz qw
 * 自定义一个任意的旋转矩阵和平移向量（可以尝试不同的值看看结果有什么变化），对轨迹１进行变换，得到一个新的轨迹２
 * 使用ICP算法（提示：取平移作为三维空间点）估计轨迹１，２之间的位姿，然后将该位姿作用在轨迹２
 * 验证：ICP算法估计的旋转矩阵和平移向量是否准确；轨迹１，２是否重合
****************************/
#include 
#include "sophus/se3.h"
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

void DrawTrajectory(vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> pose1,
                    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> pose2);

void pose_estimation_3d_3d(
    const vector<Point3f>& pts1,
    const vector<Point3f>& pts2,
    Eigen::Matrix3d& R_,
    Eigen::Vector3d& t_
);

int main()
{
     
    // path to trajectory file
    string trajectory_file = "../trajectory.txt";


    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> pose_groundtruth;
    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> pose_new;
    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> pose_estimate;
    vector<Point3f> pts_new, pts_groundtruth;

    Eigen::Quaterniond q;
    Eigen::Vector3d t;
    Sophus::SE3 T;
    string timestamp;
    ifstream textFile;

    // 自定义一个变换矩阵
    /**********************　开始你的代码，参考星球里作业５代码　****************************/
    // 旋转向量（轴角）：沿Z轴旋转45°
    Eigen::AngleAxisd rotation_vector(M_PI/4,Eigen::Vector3d(0,0,1));
    Eigen::Quaterniond rotate(rotation_vector);
   // 平移向量，可以自己自定义，我这里是 x=3, y=-1, z=0.8，可以多尝试其他值
    Eigen::Vector3d tranlation(3,-1,0.8);
    /**********************　结束你的代码　****************************/
	
    Sophus::SE3 myTransform(rotate,tranlation);
    cout<<"rotation matrix =\n"<<rotation_vector.matrix() <<endl;
    cout<<"translation vector =\n"<<tranlation <<endl;
    cout<<"myTransform =\n"<<myTransform.matrix() <<endl;

    textFile.open(trajectory_file.c_str());

    //　读取轨迹数据
    /**********************　开始你的代码，参考星球里作业８代码　****************************/
	// 提示：取平移作为三维空间点
    if(!textFile.is_open())
    {
     
        cout<<"file is empty!"<<endl;
        return -1;
    }else
    {
     
        string sLineData;
        while(getline(textFile, sLineData) && !sLineData.empty())
        {
     
            istringstream strData(sLineData);
            strData>>timestamp>>t[0]>>t[1]>>t[2]>>q.x()>>q.y()>>q.z()>>q.w();
            if(timestamp=="#" || timestamp=="-1.#INF")
            {
     
                continue;
            }

            T = Sophus::SE3(q, t);
            pose_groundtruth.push_back(T);
            pts_groundtruth.push_back(Point3d(t[0], t[1], t[2]));

            Sophus::SE3 tmp(myTransform*T); // 新的位姿
            pose_new.push_back(tmp);   
            pts_new.push_back(Point3f(tmp.translation()[0], tmp.translation()[1], tmp.translation()[2]));
        }

    }
    /**********************　结束你的代码　****************************/
    textFile.close();
    cout<<"pose_new size:"<<pose_new.size()<<"pts_new size:"<<pts_new.size()<<endl;
	
    // 使用ICP算法估计轨迹１，２之间的位姿，然后将该位姿作用在轨迹２
    /**********************　开始你的代码，参考十四讲中第７章ICP代码　****************************/
    Eigen::Matrix3d R_;
    Eigen::Vector3d t_;
    pose_estimation_3d_3d(pts_new, pts_groundtruth, R_, t_);    // 这里是书上的推导出来是第二帧到第一帧的R和t，即pts_groundtruth到pts_new的变换
    cout<<"Estimated results from ICP:"<<endl;
    cout<<"Estimated rotation matrix=\n"<<R_<<endl;
    cout<<"Estimated translation vector=\n"<<t_<<endl;
    // 取逆
    Eigen::Matrix3d Rot = R_.inverse(); // 第一帧到第二帧的旋转矩阵 即pts_new到pts_groundtruth的变换
    Eigen::Vector3d tran = -Rot*t_;     // 第一帧到第二帧的位移
    Sophus::SE3 T_estimate(Rot, tran);  // 

    // 使用我们估计的pts_new到pts_groundtruth的位姿变换pts_new-->pts_groundtruth
    for (int i = 0; i < pose_new.size(); i++)
    {
     
        pose_estimate.push_back(T_estimate*pose_new[i]);
    }
    
    /**********************　结束你的代码　****************************/

     //DrawTrajectory(pose_groundtruth, pose_new);  // 变换前的两个轨迹
    DrawTrajectory(pose_groundtruth, pose_estimate);  // 轨迹应该是重合的
    return 0;
}

void pose_estimation_3d_3d(
    const vector<Point3f>& pts1,
    const vector<Point3f>& pts2,
    Eigen::Matrix3d& R_,
    Eigen::Vector3d& t_
)
{
     
    Point3f p1, p2; // center of mass
    int N = pts1.size();
    for (int i = 0; i < N; i++)
    {
     
        p1+=pts1[i];
        p2+=pts2[i];
    }
    p1/=N;
    p2/=N;
    vector<Point3f> q1(N), q2(N);   // remove the center
    for (int i = 0; i < N; i++)
    {
     
        q1[i] = pts1[i] - p1;
        q2[i] = pts2[i] - p2;
    }

    // compute q1*q2^T
    Eigen::Matrix3d w = Eigen::Matrix3d::Zero();
    for (int i = 0; i < N; i++)
    {
     
        w+=Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z)
            *Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();
    }
    cout<<"w="<<w<<endl;

    // SVD on w
    Eigen::JacobiSVD<Eigen::Matrix3d> svd(w,Eigen::ComputeFullU|Eigen::ComputeFullV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();

    // if(U.determinant()*V.determinant()<0)
    // {
     
    //     for (int x = 0; x < 3; ++x)
    //     {
     
    //         U(x,2)*=-1;
    //     }
    // }

    cout<<"U="<<U<<endl;
    cout<<"V="<<V<<endl;

    R_ = U*(V.transpose());
    t_ = Eigen::Vector3d(p1.x,p1.y,p1.z)-R_*Eigen::Vector3d(p2.x,p2.y,p2.z);

}

void DrawTrajectory(vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> pose1,
                    vector<Sophus::SE3, Eigen::aligned_allocator<Sophus::SE3>> pose2) {
     
    if (pose1.empty()||pose2.empty()) {
     
        cerr << "Trajectory is empty!" << endl;
        return;
    }

    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));


    while (pangolin::ShouldQuit() == false) {
     
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

        glLineWidth(2);
        for (size_t i = 0; i < pose1.size() - 1; i++) {
     
            glColor3f(1 - (float) i / pose1.size(), 0.0f, (float) i / pose1.size());
            glBegin(GL_LINES);
            auto p1 = pose1[i], p2 = pose1[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }
        for (size_t i = 0; i < pose2.size() - 1; i++) {
     
            glColor3f(1 - (float) i / pose2.size(), 0.0f, (float) i / pose2.size());
            glBegin(GL_LINES);
            auto p1 = pose2[i], p2 = pose2[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }

        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }
}

附：CMakeLists.txt:

cmake_minimum_required( VERSION 2.8 )
project( ICP )

set( CMAKE_BUILD_TYPE "Release" )
set( CMAKE_CXX_FLAGS "-std=c++11 -O3" )

find_package( OpenCV REQUIRED )
# find_package( OpenCV REQUIRED ) # use this if in OpenCV2
FIND_PACKAGE(Pangolin REQUIRED)
FIND_PACKAGE(Sophus REQUIRED)

include_directories(
        ${
     Sophus_INCLUDE_DIRS}
        ${
     Pangolin_INCLUDE_DIRS}
        ${
     OpenCV_INCLUDE_DIRS}
        "/usr/include/eigen3/"
)

add_executable( ${
     PROJECT_NAME} icp.cpp )
target_link_libraries( ${
     PROJECT_NAME}
#        ${
     Sophus_LIBRARIES}
        ${
     Pangolin_LIBRARIES}
        ${
     OpenCV_LIBS}
        /home/yan/3rdparty/Sophus/build/libSophus.so
)

总结

其实就是把原始数据旋转平移一下，然后用旋转后点的数据，使用ICP估计这个旋转平移。；这个旋转是从原始位姿到新位姿的旋转，如果对其R求逆，t取负，就是新位姿到原始数据的变换矩阵，能够把新位姿复位，看是否与原位姿重合。

也可以使用g2o非线性优化方法，参考书上179页。

参考：
视觉SLAM14讲
从零开始一起学习SLAM | ICP原理及应用