动态规划算法
- 贪心算法:逐步建立一个解决方案,具体地优化一些局部准则。
- 分治:将一个问题分解成独立的子问题,求解每个子问题,并将子问题的解组合起来形成原问题的解。
- 动态规划:把一个问题分解成一系列相互重叠的子问题,并为越来越大的子问题建立解决方案。
一、weighted interval scheduling 加权区间调度
- 问题描述:每个job有开始时间、结束时间和权重,找job不overlap的最大权重。
- 解法1:最早结束时间优先。(若权重都一样,用贪心法是正确的,但在本题不对)。
- 以完成时间升序标记jobs。记p(j)=i,表示j>i,在选择job j后,可选的最大下标为i。
记OPT(j)表示由作业1,2,3…j组成的请求的最优解。
若OPT选择j,wight包括vj,包括之前的OPT:1,2,…p(j);
若OPT不选择j,一定包括OPT:1,2…j-1

- 解法2:暴力法
//伪代码
输入:n,s[n],f[n],v[n]
排序:根据f[n]
计算:p[n]
int computeOpt(int j){
if(j==0)
return 0;
else
return max(v[j]+computeOpt(p[j]),computeOpt(j-1));
}
分析:分层递归调用,时间复杂度指数级增长。
解决:存储每个子问题的计算结果,以备查找之需。
//伪代码. O(nlogn) time |
输入:n,s[n],f[n],v[n];
排序:根据f[n];//O(nlogn)
计算:p[n];
定义:m[n], m[0]=0;
int mComputeOpt(int j){
//每次调用O(1) time ,总共O(n) time
if(m[j] is empty)
m[j]=max( v[j]+mComputeOpt(p[j]) , mComputeOpt(j-1) );
return m[j];
}
分析:时间复杂度O(nlogn),若已由开始时间、结束时间排序O(n)。
- 解法3:用DP算法计算最优的区间集。
findSolution(int j){
if(j==0)
return {
};
else if(v[j]+m[p[j]]>m[j-1])
return {
j} ∪ findSolution(p[j]);
else
return findSolution(j-1);
}
分析:由于递归调用次数<=n ,因此时间复杂度为O(n)。
- 解法4:自底向上的动态规划,展开递归。
//伪代码
bottomUp(int n,int s[],int f[],int v[]){
sort(f[n]);
compute p[n];
int m[n];m[0]=0;
for(int i=1;i<=n;i++)
m[i]=max( v[i]+m[p[j]] , m[i-1] );
}
- 实现:
#include 二、segmented least squares 分段最小二乘法
- 最小二乘:统计学基本问题——给定n个点(坐标(xi,yi)),找到一条线y = ax + b使误差的积分到达最小。
- 问题:有n个点和一个常数c,找到一系例的线,满足min f(x)=E+cL.
E=每个线段的误差之和;L=线的数量。 - 动态规划解决思路:
记OPT(j)=点p1…pj的最小误差之和。
e(i,j)=点pi…pj的最小平方和。
- 算法:
selectedLeastSquares(int n,int p[n],int c){
for(int j=1;j<=n;j++)
for(int i=1;i<=j;i++)
计算e(i,j);
int m[maxn];m[0]=0;
for(int j=1;j<=n;j++)
m[j]=min{
eij+c+m[i-1]} ,1<=i<=j
return m[n]
}
- 分析:O(n3) time | O(n2) space
每次计算e(i,j) O(n2) time ,共计算n次
改进:通过预计算,改善为O(n2) time | O(n) space
三、knapsack problem 背包问题
- 问题描述:给定n个物品和1个背包。每个物品i有重量wi和价值vi;背包可承重W;目标:找背包可放入物品的最大价值。
- 贪心算法无法解决:①以价值从大到小放×②以重量从小到大放×③以vi/wi从大到小放×
- 动态规划解法:
定义OPT(i,w)=物品1,2…i的可放入承重w的背包的最大价值
对于第i个物品:
①若i不放入背包:OPT(i,w)=OPT(i-1,w)
②若i放入:OPT(i,w)=OPT(i-1,w-wi)+v[i]
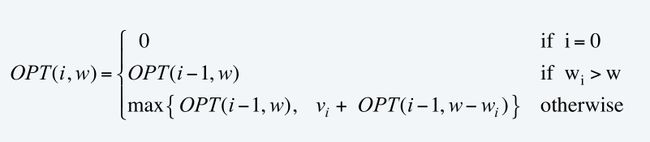
//bottom-up
//O(n*W) time | O(n*W) space
int knapsack(int n,int W,int w[n],int v[n]){
int OPT[maxn][maxn];
//OPT(i,w)=0;if(i==0)
for(int j=0;j<=W;j++)
OPT[0][j]=0;
//OPT(i,w)=OPT(i-1,w);if(w
//OPT(i,w)=max( v[i]+OPT(i-1,w-wi) , OPT(i-1,w));else
for(int i=1;i<=n;i++){
for(int j=1;j<=W;j++){
if(w[i]>j)
OPT[i][j]=OPT[i-1][j];
else
OPT[i][j]=max( v[i]+OPT[i-1][j-w[i]] , OPT[i-1][j]);
}
}
return OPT[n][W];
}
- 算出最优值后,可以回溯找到解。
四、RNA secondary structure RNA二级结构
- RNA:string b;b由字母{A,C,G,U}组成。
- 二级结构:RNA是单链的,有环(每对的末端至少间隔4个字母)、与自身形成碱基对(A-U or G-C)。
- 问题描述:给定一个RNA序列,找到一个二级结构,使碱基对的数量最多。
- 记OPT(j)=b1,b2…bj中最多碱基对。
记OPT(i,j)=bi…bj中最多碱基对。 - 选择匹配bt-bn
查找结构(b1,b2…bt-1)=OPT(t-1)和bt+1,bt+2…bn-1。
五、sequence alignment 序列比对
- 记gap 为 δ,没匹配(不一样)为αpq。
cost=δ+αCG+αTA 。 - 应用:语音识别、生物学计算、unix diff。
- 序列对比:给定两个string,找到Min cost。
- 定义:OPT(i,j)=Min cost of string x 1 x 2 … x i and y 1 y 2 … y j .
①若xi有对应yj,OPT(i,j)=( xi-yj ) +OPT(i-1,j-1)
②若xi无对应,OPT(i,j)=δi +OPT(i-1,j)
③若yj无对应,OPT(i,j)=δj +OPT(i,j-1)
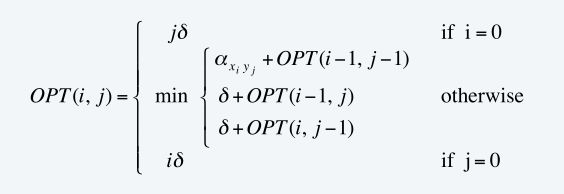
- 算法:
//伪代码
int sequenceAlignment(int m,int n,int x[m],int y[n],int δ[],int α[][]){
//if j=0
for(int i=0;i<m;i++)
OPT[i,0]=δ[xi];
//if i=0
for(int j=0;j<n;j++)
OPT[0,j]=δ[yj];
//otherwise
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
OPT[i][j]=min(α[xi][yi]+OPT[i-1][j-1],δ[xi]+OPT[i-1][j],δ[yj]+OPT[i][j+1]);
}
}
return OPT[m][n];
}
- 分析: Θ(mn) time | Θ(mn) space.
- 练习:C:Human Gene Functions
#include- 总结:1.C++数组下标可以是字符(ASCII码:a-97,A-65, - 45)
2.数组及赋值,可以放在一个函数中,main中再调用一次即可。
3.char c[5];
scanf("%s",c+1);//用指针的方式,传入一个字符串(从c[1]开始),直到遇到空格结束。
cin>>c+1;//同上
4.max对比多个数:max(a,max(b,c));
六、Hirschberg’s algorithm 赫施伯格算法——序列对比算法的空间优化
1、序列对比算法空间复杂度可以是线性
- O(m*n) time | O(m+n) space
- 结合分治算法和动规算法
2、算法内容
- 假设有一张距离图,f(i,j)=(0,0) to (i,j)最短路径
- 则对于所有i 、j满足f(i,j)=OPT(i,j)。(对于长度为m,n的A,B字符串,我们可以视为一个 ( m + 1 ) ∗ ( n + 1 ) (m+1)*(n+1) (m+1)∗(n+1)的矩阵。走斜边表示两个字符match,向右或者向下表示该字符gap。要求两个字符串的最小匹配值,也即是从 ( 0 , 0 ) (0,0) (0,0)到 ( m + 1 , n + 1 ) (m+1,n+1) (m+1,n+1)的最小距离。)
- 可以以O(mn) time | O(m+n) space ,计算f(,j)
- 可以反转方向(右下到左上)&反转(0,0)和(m,n)角色进行计算。
- 假设g(i,j)=(i,j) to (m,n)的最短路径
可以以O(mn) time | O(m+n) space ,计算g(,j) - 可以使用点(i,j)计算(0,0) to (m,n)的最短路径=f(i,j)+g(i,j)
- 假设q坐标可以使 f (q, n/2) + g (q, n/2)最小,那么可以使用点 (q, n/2)计算 (0, 0) 到 (m, n) 的最短路径。
- 使用分治法寻找q:
分:对xq和yn/2排序;
治:递归计算每轮最优解。
3、实现
参考
七、Bellman-Ford algorithm 贝尔曼-福特算法
1、定义
- [def]负权回路:一个有向环,边的权重相加为负数。
- [lemma1]:若点v到t之间存在负环,则不存在点s到t的权重和最小的路径。
- [lemma2]:若点v到t之间不存在负环,则一定存在点s到t的权重和最小的路径(有
2、问题描述
- 最短路径问题:给定一个有向图G=(V,E),每个点有权重cvw(c有可能为负数,但没有负环),找到点s到t的权重和最小的路径。
- 负环问题:给定一个有向图G=(V,E),每个点有权重cvw,找到一个负环(如果存在的话)。
3、思路
- 解答尝试:
1.基于贪心算法的dijkstra处理不了带有负权值的边的图。×
2.重新赋权重法:将所有边加同一个常数,使图中不存在负数边。× - 动态规划算法:
- 状态表示
OPT(i,v)=使用<=i条边,点v到t的最廉价路径。 - 状态转移
①若使用了<=i-1条边,OPT(i,v)=OPT(i-1,v)。
②若使用了恰好i条边,假设v到w为路径的第一条边(由于可能有多条与v点直接相连的点,所以w点可能有多个)。OPT(i,v)=min(OPT(i-1,w)+cvw)。
OPT(i,v)=min( OPT(i-1,v) , min(OPT(i-1,w)+cvw ) )
- 状态结果
OPT(n-1,v)=点v到t路径的min cost。
4、应用
Bellman算法,检查图中是否有正权回路。
正权回路:一个有向环,边的权重相加为正数。
POJ:Currency Exchange
5、分析
O(m*n) time | O(n2) space
m——边数;n——点数。
八、distance vector protocols 距离向量协议
九、negative cycles in a digraph 有向图中的负圈
参考文献:普林斯顿算法分析PPT
