《异常检测——从经典算法到深度学习》7 基于条件VAE异常检测
《异常检测——从经典算法到深度学习》
- 0 概论
- 1 基于隔离森林的异常检测算法
- 2 基于LOF的异常检测算法
- 3 基于One-Class SVM的异常检测算法
- 4 基于高斯概率密度异常检测算法
- 5 Opprentice——异常检测经典算法最终篇
- 6 基于重构概率的 VAE 异常检测
- 7 基于条件VAE异常检测
- 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测
- 9 异常检测资料汇总(持续更新&抛砖引玉)
- 10 基于条件 VAE 的鲁棒无监督KPI异常检测
- 11 针对大量出现的KPI流快速部署异常检测模型
相关:
VAE 模型基本原理简单介绍
7. 基于条件VAE异常检测
论文名称:Anomaly Detection With Conditional Variational Autoencoders
发表时间:2019.12 立即下载
论文总体结构:
-
INTRODUCTION :引出并总体介绍CVAE,概括论文亮点,介绍论文结构。
-
PROBLEM STATEMENT:简单陈述问题,引出需要的解决方法。
-
BACKGROUND AND PROPOSED METHOD:介绍 VAE、CVAE 、CVAE 异常检测的度量方法、VAE 异常检测。
-
EXPERIMENTS ON BENCHMARKS :基于 MNIST 与 Fashion-MNIST 的异常检测实验、综合问题。
-
EXPERIMENTS ON CMS TRIGGER RATE MONITORING:基于CMS数据的实验。
-
CONCLUSIONS AND FUTURE WORK:总结
7.1 INTRODUCTION
7.1.1 总体介绍 CVAE (Conditional Variational Autoencoders)
CVAE是一种条件有向图模型,输入观测值对产生输出的隐变量的先验值进行调制,以便将高维输出空间的分布建模为以输入观测值为条件的生成模型。
CVAE is a conditional directed graphical model where input observations modulate the prior on latent variables that generate the outputs, in order to model the distribution of high-dimensional output space as a generative model conditioned on the input observation
这种定义性质的话可能并不那么容易理解,但是通过结合图模型可能可以方便很多。
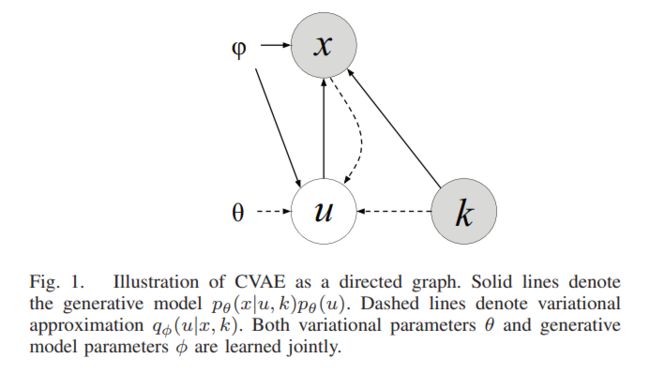
其中的实现表示生成模型 p θ ( x ∣ u , k ) p_\theta {(x|u,k)} pθ(x∣u,k),虚线表示变分似然 q ϕ ( u ∣ x , k ) q_\phi{(u|x,k)} qϕ(u∣x,k)。其中 θ \theta θ 和 ϕ \phi ϕ 都是变分参数,与 VAE 训练过程是相同的,分别在 decode 和 encode 过程中生成。
与 VAE 模型相比,多了另外参数 k ,可以认为这是额外的输入数据(extra input),也可以认为是条件,在多了 k 的影响下,VAE 便成了 Conditional VAE.
如果对 VAE 有所了解的话,那么理解 CVAE 就非常简单了。
推荐参考:
- VAE 模型基本原理简单介绍
- Conditional Variational Autoencoders
7.1.2 概括论文亮点 (Contributions)
- 定义了新的损失函数 (loss function),让模型能够学习最佳重构方案( reconstruction resolution)。
- 设计新的与 CVAE 相关联的异常度量指标,在经典机器学习和粒子物理特定数据集上都具有了优异的性能。
- 提出基于MNIST数据集,新的异常检测实验方案。
7.2 问题陈述
首先论文吐槽了一下没找到合适的数据集,所以不得不选择了手写数字数据集 (MNIST)。
然后给出条件 k k k(已知),输入数据 x x x,以及隐变量 u u u (未知) 之间的关系 x = f ( k , u ) x = f(k,u) x=f(k,u) 。
对于很多观测数据 X = [ x 1 , x 2 , . . . , x n ] X=[x_1,x_2,...,x_n] X=[x1,x2,...,xn],我们需要重点观测的实例包括:
- 单一特征的大变化,我们称之为 A 类型异常;
- 变化小但是系统化的特征,我们称之为 B 类型 异常。
不需要着重观测的数据:
- 不相关特征且严重程度较小
总之,我们需要一种算法,利用数据中已知的因果结构,找出上面列出的两种类型的问题,将其推广到不可见的情况,并使用数据而不是依赖于特征工程。在目标应用程序的上下文中,推理时间可以忽略不计。
7.3 背景介绍与方法提出
7.3.1 VAE & CVAE
VAE 基本原理在 VAE 模型基本原理简单介绍 已经比较详细的介绍了,这里只介绍对 VAE 模型的改进部分(CVAE)。
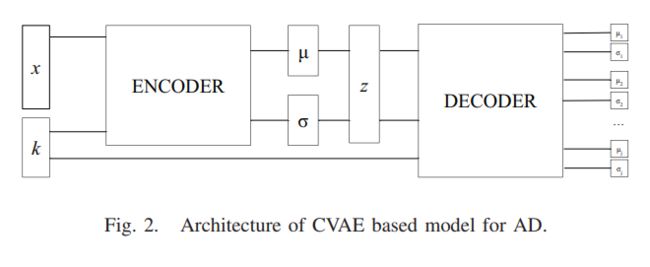
通常情况下训练 VAE 模型时,使用 MSE ( mean squared error ) 来计算输入数据 x 与 decoder 生成数据之间的差异。
计算差异的公式可以由正态分布概率密度函数推导:
f ( x ) = 1 2 π σ e x p ( − ( x − μ ) 2 2 σ 2 ) ( 1 ) f(x)= {1\over \sqrt {2\pi}\sigma} exp(-{(x-\mu)^2\over 2\sigma^2}) \ \ \ \ \ \ \ \ (1) f(x)=2πσ1exp(−2σ2(x−μ)2) (1)
取对数后,得
log f ( x ) = log 1 2 π σ + ( − ( x − μ ) 2 2 σ 2 ) log f ( x ) = − log 2 π σ − ( x − μ ) 2 2 σ 2 ( 2 ) \log f(x) = \log {1\over \sqrt {2\pi}\sigma} + (-{(x-\mu)^2\over 2\sigma^2})\\ \log f(x) = -\log {\sqrt {2\pi}\sigma} -{(x-\mu)^2\over 2\sigma^2} \ \ \ \ \ \ (2) logf(x)=log2πσ1+(−2σ2(x−μ)2)logf(x)=−log2πσ−2σ2(x−μ)2 (2)
这篇论文认为,认为可以固定方差 σ = 1 \sigma = 1 σ=1。当 σ = 1 \sigma =1 σ=1 时,极大似然的 log 值计算公式为:
However, this is equivalent to setting the observation model pθ(x|z) as a normal distribution of fixed variance σ = 1. Indeed, the log-likelihood of a normal distribution with fixed variance of 1 is given as:− log N ( x ; μ , 1 ) = ∣ ∣ x − μ ∣ ∣ 2 + log ( 2 π ) ( 3 ) -\log \N(x;\mu,1)=||x-\mu||^2+\log(\sqrt{2\pi}) \ \ \ \ \ \ \ \ (3) −logN(x;μ,1)=∣∣x−μ∣∣2+log(2π) (3)
注:从公式(2) 到公式(3) 存在问题,即代入 σ = 1 \sigma =1 σ=1 ,原来的式子(2)应该多一项 1 2 1\over 2 21,也就是说,导入后正确结果是:
− log N ( x ; μ , 1 ) = ∣ ∣ x − μ ∣ ∣ 2 2 + log ( 2 π ) ( 4 ) -\log \N(x;\mu,1)={||x-\mu||^2\over 2}+\log(\sqrt{2\pi}) \ \ \ \ \ \ \ \ (4) −logN(x;μ,1)=2∣∣x−μ∣∣2+log(2π) (4)
很明显,这样的假设 ( σ = 1 \sigma=1 σ=1) 是存在很大的问题的,初始化若干个正态分布,然后根据数据特征的实际情况而进行调整数据特征的均值和方差。如果直接添加这项限制,对 VAE 的随机性特征会有很大限制。
但除非事先知道数据的相关信息,否则数据的分布是不需要很大的特征振幅。
所以可以通过学习MSE重构的方差,模型可以找到重建数据的每个特征的最佳误差方案,从而从相关性中分离固有噪声。这在经验上给出了类似的结果,关联一个微调的加权参数,同时消除了调整所述超参数的需要。
7.3.2 CVAE 改进部分
CVAE 结构中,有三种类型的变量(参见图1)。对于随机可观测变量 x x x, u u u(未知,未观测)和k(已知,观测)是独立的随机隐变量。
条件似然函数 p θ ( x ∣ u , k ) p_\theta{(x|u,k)} pθ(x∣u,k) 是非线性转换而来的, ϕ \phi ϕ 是另一个非线性函数,近似于推理后验 q ϕ ( u ∣ k , x ) = N ( μ , σ I ) q_\phi{(u|k,x)}=N(\mu,\sigma I) qϕ(u∣k,x)=N(μ,σI).
隐变量 u u u 允许在 x x x 与给定 k k k 的条件分布下对多个模式进行建模,使得该模型足以对一个相互映射进行建模。
为了近似 ϕ \phi ϕ 和 θ \theta θ ,对 ELBO 进行调整:
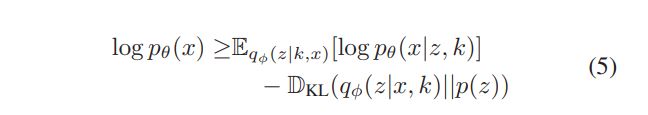
其中隐变量 z z z 用于捕捉不可观测的变异因子 u u u .
损失函数为:
注:如果不了解 ELBO 的话,请参考 VAE 模型基本原理简单介绍 。
我们的模型虽然是基于 CVAE 但是着重于异常检测输出变量的条件分布。
我们使用Keras和TensorFlow作为后端,使用Adam优化器和早期停止准则训练模型。一旦模型参数被学习,我们就可以使用不同的度量来检测异常:
- A 类问题:从隐变量 z z z 采样,通过计算重构损失 ∣ ∣ 1 σ ( x − x ^ ) 2 ∣ ∣ ∞ ||{1\over \sigma} {(x-\hat x)^2}||_\infty ∣∣σ1(x−x^)2∣∣∞。
- B 类问题:通过计算KL平均散度。
7.3.3 CVAE 异常检测的一种度量
对于给定数据 (x,k),VAE 的评估方法 L ( x , k ) L(x,k) L(x,k) 是 l o g p θ ( x ∣ k ) log\ p_\theta{(x|k)} log pθ(x∣k) 的近似上限,测量x与给定k的模型之间的差异。因此,对这种损失的价值进行阈值化是处理AD的一种自然方法。因此,CVAE在这里提供了一个模型,可以自然地估计x是如何异常的,而不是计算(x,k)的异常程度。这意味着如果存在一个稀有的k值和一个适当的x值相关联,那么应该被视为正常的。
方程6中的损失函数,可以分解为两个独立问题。由于两个独立的异常场景,我们不会组合各个指标到一个总体得分中,而是使用逻辑 O R OR OR 来确定异常实例。
- 第一种情况,我们对识别单个特征上的异常感兴趣。当大多数特征没有表现出异常并降低异常分数时,通常使用的重建误差均值可能是一个错误的选择.
- 第二种情况,我们期望 μ z μ_z μz落在异常情况下分布的尾部。如[11]中所述, D K L D_{KL} DKL 度量了表示后验分布所需的额外信息量,给定了用于解释当前观察结果的隐变量的先验值。 D K L D_{KL} DKL 的绝对值越低,观察到的状态越可预测。
最后,VAE 的使用让该方法可以推广到文献[12]中所讨论的不可见的观测值问题。
[11] Mevlana Gemici, Chia-Chun Hung, Adam Santoro, Greg Wayne, Shakir Mohamed, Danilo J Rezende, David Amos, and Timothy Lillicrap. Generative temporal models with memory. arXiv preprint arXiv:1702.04649, 2017.
[12] Durk P Kingma, Shakir Mohamed, Danilo Jimenez Rezende, and Max Welling. Semi-supervised learning with deep generative models. In Advances in NeurIPS, pages 3581–3589, 2014.
7.3.4 VAE 异常检测
这一部分总体上介绍了基于VAE 的异常检测一些方法。
这里暂时略过了,如有需要可以仔细了解。
7.4 实验
7.4.1 基于MNIST & Fashion-MNIST 的异常检测
首先解释了一下为什么用这两个数据集(略)。
其次,论文对异常的定义与很多论文不同。一般情况下 MNIST 数据集用于异常检测是把某个数字对应的数据看作异常,其他的作为异常。
这篇论文中,使用 LeNet-5 对数据进行分类,再用 LeNet-5 算法与人为指定的阈值进行分类,分类后的结果作为这次CVAE实验的数据集。
下面的图片是使用不同分类算法提出来的它们认为可能是异常的数据。最终实验时只采用了 LeNet-5 的分类结果。

实验中,我们给向量 k k k 指定了一个类标签,而 u u u 应该包含关于其他变化因素的信息,例如用来写数字的手。检测异常的问题类似于 B型问题。在这种情况下,我们期望 μ ( D K L ) \mu(D_{KL}) μ(DKL) 在标签错误或不常见的情况下会更高。
在实验中,选取了10,000 个样本作为测试集。如下图所示,实验把 CVAE 算法与其他三种算法进行了比较。左图是基于 MNIST 的实验结果,右图是基于 Fashion-MNIST 的实验结构。

7.4.2 合成问题
合成的数据集使用了正态分布( μ = 0 \mu = 0 μ=0, σ = 1 \sigma = 1 σ=1),连续并且相互独立的隐变量 u u u 和 k k k。可观测的 x x x 仅仅是 u u u, k k k 和其他噪声 ϵ \epsilon ϵ 共同生成的: x j = f j ( μ → ) ⋅ ∑ i = 0 m S j i k i + ϵ x_j = f_j{(\overrightarrow{\mu})} \cdot \sum_{i=0}^{m}{S_{ji}k_i}+\epsilon xj=fj(μ)⋅∑i=0mSjiki+ϵ,
其中
* j j j 是 x → \overrightarrow x x 的索引。
- 二元矩阵 S S S 是描述了哪一个 k k k 用于计算特征 j j j。

- 函数 f ( u → ) f(\overrightarrow u) f(u) 描述了哪个 u u u 进入了定义每个特征 j j j 的产品: f j ( u → ) = ∏ o u o f_j(\overrightarrow u)= \prod_{o} u_o fj(u)=∏ouo。
对每个样本, S S S 和 f ( u → ) f(\overrightarrow u) f(u) 保持不变,而 k k k 和 u u u 发生改变。为简单起见,我们确保每个 j j j 只依赖于一个 k k k 并且依赖是均匀分布的。最后,我们可以操作 o o o 和 m m m 的值。例如,第一列 x 0 x_0 x0 可以用 k 0 k_0 k0, u 1 u_1 u1 和 u 4 u_4 u4表示: x 0 = k 0 u 1 u 4 x_0=k_0u_1u_4 x0=k0u1u4; x 9 9 x_99 x99 可能通过 k 4 k_4 k4, u 0 u_0 u0 生成等等。
我们生成 x x x 为100维 ( n = 100 n = 100 n=100) 且 m = o = 5 m = o = 5 m=o=5 的样本。相关矩阵的一个例子如下图(图5)所示。

对于测试,我们根据 表 I 生成样本。选择 5 σ \sigma σ 和 3 σ \sigma σ来自于我们的目标应用程序的遗留需求。该异常检测算法的执行方式是:
-
A类问题: 比较 decoder 的输出和 encoder 的输入,以发现仅在一个特征上观察到的问题 ;
-
B类问题:比较属于相同因果关系组(即输入时使用相同的 k k k 值)的样本的所有特征的 D K L D_{KL} DKL 域。

两个问题对应的ROC曲线如图6(下图)所示。给定A型异常的高阶偏差,算法很容易发现这些类型的问题。在层次结构的背景下,算法需要建立一个映射模型,从单一输入到多个可能的输出。
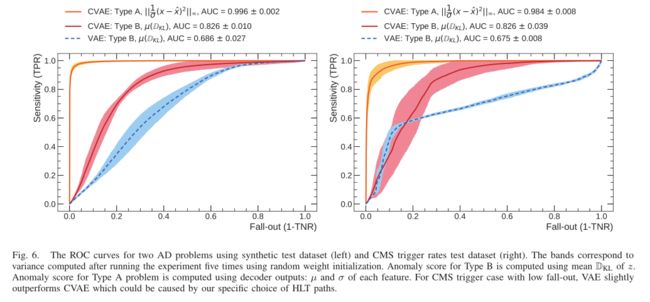
如 [3] 中讨论我们需要能够进行不同预测的模型,B类问题给出了良好的结果,优于普通的 VAE ,证明了CVAE 适合这样的任务。[3] Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning structured output representation using deep conditional generative models. In Advances in neural information processing systems, pages 3483–3491, 2015.
7.5 基于 CMS 的实验
7.5.1 动机
这项工作的出现直接从明确的紧急监测的CMS[29]实验。CERN LHC[30 ]的CMS实验以每秒4000万次粒子碰撞(事件)的惊人速度运行。每个事件对应大约1 MB未处理的数据。由于可以理解的存储限制和技术限制(例如,足够快的电子读出),这个实验需要实时地将记录的数据数量从每秒4000万件减少到1000件。为了达到这个目的,一组被统称为触发器系统的分层算法被用来处理和过滤进入的数据流,这是物理事件选择过程的开始。
触发算法[31]旨在降低事件率,同时保持实验的物理范围。CMS触发系统的结构分为两个阶段,使用越来越复杂的信息和更精细的算法:
- L1 触发:在定制设计的电子产品上实施; 把输入速率从 40 MHz 减少到 100 kHz, 时间小于 10 μ \mu μs。
- 高等级触发(HLT):一个在计算机场上运行的碰撞重建软件;将L1触发器的100 kHz速率输出降低到1 kHz ,时间小于 300 ms
L1和HLT系统都实现了一组规则来执行选择(称为路径)。HLT是由一组可配置的L1触发路径选择的事件来种子的。
在典型的运行条件下,触发系统可以调节观测到的碰撞产生的海量数据。通过对每个检测器子系统的独立监控,保证了记录数据的质量(比如说电压),通过监控触发率事件接受率会受到问题数量的影响,例如检测故障,软件问题等。根据问题的性质,与特定路径相关的比率可能会改变到不可接受的水平。危急情况包括降到零或增加到极值。在这种情况下,系统应该向值班人员发出警报,要求进行问题诊断和干预。
HLT路径通常是非常强相关的。这是由于一组路径选择了类似的物理对象(因此重构了相同的事件)和/或通过L1触发路径的相同选择来种子。奇异路径的速率偏差临界水平应视为异常,而随机触发路径数量上的偏差较小则可能是统计波动的结果。另一方面,在一组由类似物理或使用相同硬件基础设施相关的触发路径上的可观察到的相干漂移(甚至很小),是在触发系统或硬件组件中可能存在故障的指示。
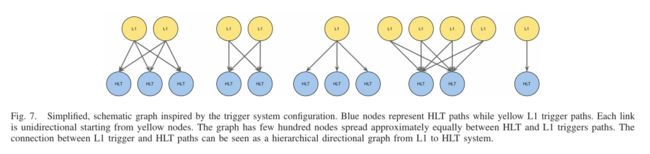
我们在算法中探索了这种层次结构。每个HLT路径都有一个直接的、预先配置的链接,通过指定的配置链接到一组L1触发器路径,如图7(下图)所示。配置变化很少,例如节点被添加、禁用或更正。因此,HLT系统的性能直接与L1触发器的状态有关。
我们不关注最小化推断时间,因为异常可以在几分钟内标记出来,这对于所有考虑的算法来说已经足够长了。
[29] Serguei Chatrchyan et al. The CMS experiment at the CERN LHC. JINST, 3:S08004, 2008.
[30] The LHC Study Group. The Large Hadron Collider, conceptual design. Technical report, CERN/AC/95-05 (LHC) Geneva, 1995.
[31] V ardan Khachatryan et al. The CMS trigger system. JINST, 12(01):P01020, 2017
7.5.2 实验
把 HLT 速率用作 x x x,把 L1 触发率 用作 k k k,我们的原型使用了4条L1触发路径,每条都包含6条唯一的HLT路径。我们仅从配置中存在所有选择路径的样本中提取速率。最终得到102895个样本,然后将样本分为训练集、验证集和测试集,我们的测试集有2800个样本。操作人员为每个 CMS 子检测器和每个样本设置质量标签。由于全局质量标志是由所有子系统的贡献组成的,一个样本可以被认为是坏的,因为与我们选择的触发路径集无关的检测器组件的性能不佳,或者与我们试图解决的问题无关。因此,我们不能在测试集中使用这些标签。相反,我们考虑可能在生产环境中发生的假想情况,类似于用于合成问题的情况。我们以与合成数据集相似的方式操作我们的测试集,生成四个合成测试数据集。我们检测一个HLT路径上的孤立问题-类型A;在同一L1触发路径上的HLT路径存在问题-类型B。
我们将结果报告在图6中。该算法在CMS数据集上的性能与合成算法的性能相当。CMS实验目前没有提供任何工具来跟踪属于B类的问题。鉴于所提方法的良好性能,我们相信可以考虑部署该解决方案,并在生产环境中提供进一步的测试和改进。
7.6 总结
本文介绍了利用 CVAE 异常样本的方法。结合CMS触发率监控的具体案例,对现有的监控功能进行了扩展,显示了良好的检测性能。该算法不依赖于训练时的合成异常,也不依赖于附加的特征工程。我们证明了该方法不受CMS实验的限制,并且具有跨不同领域工作的潜力。然而,需要对更困难的数据集进行更多的测试,比如说在 CIFAR,提供了更多的类和更高的方差。我们没有对任何实验进行超参数扫描,因此我们期望进一步优化后的结果会更好。后续研究预测使用CMS触发器系统的完整配置。该方法的一个有趣的扩展是学习潜存空间中未知变化因素的正确编码,这在目前是不受限制的(例如MNIST数据集中数字的倾斜或粗体)。
7.7 相关代码
复现论文思路的代码很难,如果有小伙伴找到对应的代码实现,欢迎分享在下方的评论中。感谢!
首先提出两个重要假设:
- Conditional VAE 结构中的 Condition 结构及具体数值必须根据实际情况调整。
- Conditional VAE 不一定需要额外的输入,但是需要额外的条件。论文中图2 中输入层 含有的 k k k 以及 博客 https://ijdykeman.github.io/ml/2016/12/21/cvae.html 提到的 CVAE 中的条件不一定是指输入时的条件,也可以是隐变量映射的高斯分布的一些特征条件。比如说论文中提到,定义方差等于1,这也是一种 condition。对隐变量映射的高斯分布所加的一些约束条件。
关于 CVAE 的代码部分这里暂时没有合适的例子,有时间的话再补上。另外分享一下找到的相关的另外一份代码,推荐了解一下,请关注里面的 condition 具体指的是什么。https://github.com/amunategui/CVAE-Financial-Anomaly-Detection
Smileyan
2020.11.25 15:33

