概率论与数理统计(1):随机事件与概率

概率论与数理统计(1):随机事件与概率

此系列博客是出于想要锻炼自己形成知识体系的能力的目的，在备考过程中整理，
参考教材为《概率论与数理统计》.机械工业出版社.孙振绮 主编、《概率论与数理统计》.高等教育出版社.盛骤 编

一.随机事件

1.随机试验

随机试验特点：

①可重复性：可在相同条件下重复进行

②可观察性：每次试验可能结果不止一个，并能事先明确所有可能结果

③随机性：进行一次试验之前不能确定哪一个结果会出现

例如：抛一枚硬币，观察出现正面的次数；

2.定义1（样本空间，样本点）

​ 随机试验的每一个可能的结果，称为一个样本点e或ω，所有样本点组成的集合称为样本空间S或Ω
​ **注：**样本点也称为基本事件
​ 例：写出样本空间
​ ·掷一枚硬币，观察正、反面出现的情况：
​ e₁=“正面”,e₂=“反面” ，S={e₁,e₂}
​ ·掷一枚骰子，观察点数
​ S={1,2,3,4,5,6}
​ `观察某城市某月内交通事故发生次数
​ S={0,1,2,…}
​ ·从一批灯泡中随机地抽取一只灯泡，测试其寿命t
​ S={t|t≥0}
​ ·对目标进行射击，直到击中为止，1表示击中，0表示未击中，记录射击结果
​ S={1,01,001,0001,…}

3.定义2（随机事件）

​ 样本空间S的任意一个子集A，称为一个随机事件，简称“事件”
​ 注：事件A发生即在一次试验中，事件A中的某个样本点出现

二.事件的关系与运算

​ 事件是集合，故事件间的关系与事件的运算按照集合论中集合之间的关系和集合运算来处理
​ 而在概率论中，这些运算有其在概率论中的提法，可以根据“事件发生”的含义，给出它们在概率论中的含义

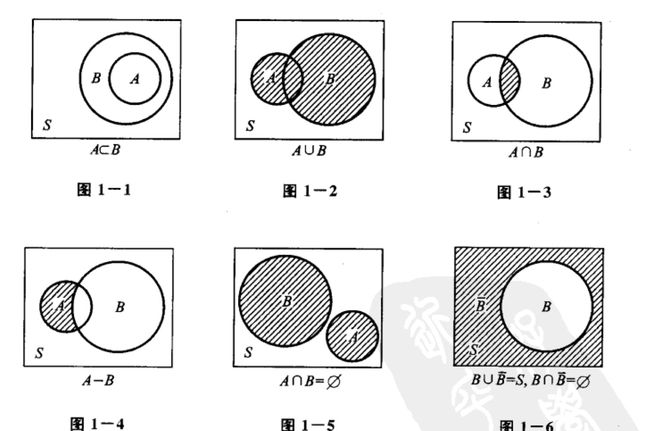
1.事件的包含：A⊂B

​ 事件A发生时，事件B一定发生

2.事件的相等：A=B

​ 若A⊂B，且B⊂A，则称事件A与B相等

3.事件A与B的并（和）

​ A∪B（或A+B) = “事件A,B至少有一个发生”

​ n个事件的并：=”事件A₁,A₂,…,A_n至少有一个发生“
​ 可数个事件的并：=“事件A₁,A₂,…至少有一个发生”

4.事件A与B的交（积）

​ A∩B（或AB）=“事件A,B同时发生”

​ n个事件的交：=”事件A₁,A₂,…,A_n同时发生“
​ 可数个事件的并：=“事件A₁,A₂,…同时发生”

5.互斥事件 AB=∅：A,B不能同时发生

6.对立事件：=S-A=“事件A不发生”

性质：事件A与B对立AB=∅ 且A∪B=S

​ 对立事件互斥事件
​ 互斥事件对立事件

7.事件A与B的差

A-B=“事件A发生，B不发生”=

8.事件的运算律

①交换律：

$$A\cap B=B\cap A,A\cup B=B\cup A$$

②结合律：

$$(AB)C=C(AB),(A\cup B)\cup C=A\cup (B\cup C)$$

③分配律：

$$A(B\cup C)=AB\cup AC,A\cup (BC)=(A\cup B)\cap (A\cup C)$$

④摩根律：

$$\overline{A\cap B}=\overline{A}\cup \overline{B},\overline{A\cup B}=\overline{A}\cap \overline{B}$$

$$\overline{{\cup }_{i=1}^n{A}_i}={\cap }_{i=1}^n\overline{A_i},\overline{{\cap }_{i=1}^n{A}_i}={\cup }_{i=1}^n\overline{A_i}$$

总结一下摩根律，即为：交的补=补的并，并的补=补的交

​ （长横变短横，开口调个头）

三.古典概率

1.定义1（概率）

​ 事件A发生可能性大小的数值，称为A的概率，记为P(A)

2.定义2（古典概率）

​ 样本空间满足有限性（只有有限个样本点）和等可能性（每个样本点出现的可能性相等）的随机试验为古典概型试验，事件A的概率：
$$

$$

$$P(A)=\frac{A包含的样本点数}{S包含的样本点总数}$$

3.定理1（古典概率性质）

​ （1）P(∅)=0 ,P(S)=1
​ （2）0≤P(A)≤1
​ （3）若A，B互斥，即AB=∅则P(A+B)=P(A)+P(B)

推广：若A₁,A₂,…,A_n两两互斥，则P(A₁+A₂+…+A_n)=P(A₁)+P(A₂)+…+P(A_n)

4.加法公式

$$P(A\cup B)=P(A)+P(B)-P(AB)$$

$$P(A_1\cup A_2\cup A_3)=P(A_1)+P(A_2)+P(A_3)-P(A_1{A}_2)-P(A_1{A}_3)-P(A_2{A}_3)+P(A_1{A}_2{A}_3)$$

5.减法公式

$$P(A-B)=P(A\overline{B})=P(A)-P(AB)$$

​ 若B⊂A，则P(B)≤P(A)，且P(A-B)=P(A)-P(B)

6.对立事件

$$P(\overline{A})=1-P(A)$$

7.常用基本结论

①排列组合

$$排列：A_n^k=\frac{n!}{(n-k)!}$$

$$组合：C_n^k=\frac{n!}{(n-k)!k!}$$

②加法原理

③乘法原理

④允许重复的排列

​ 从n个不同元素中有放回的抽取k个，按照一定顺序排成排列，有n·n…n=n^k种排列方法

四.几何概率

1.定义

​ 设区域G是平面区域Ω的一部分，若向Ω内投掷一个质点，质点落入G内的概率为
$$P(G)=\frac{S_G}{S_{\Omega }}$$

2.计算方法

​ 确定区域的测度，计算长度、面积或体积

五.统计概率

1.定义1（频率）

​ 在n次试验中，若事件A发生了n_A次,则称
$$f_n(A)=\frac{n_A}{n}$$
为事件A发生的频率

2.定义2(统计概率)

​ 在相同条件下重复进行的试验中，若随着试验次数增加，事件A发生的频率稳定在常数p附近，则称p为A的概率

3.定义3（概率的公理定义）

​ 设随机试验的样本空间为S，对于每个事件A，定义P(A)，满足：

①非负性：P(A)≥0
②规范性：P(S)=1
③可加性：若事件A₁,A₂,…A_n两两互斥，则
$$P(A_1+A_2+...+A_n)=P(A_1)+P(A_2)+...+P(A_n)$$
则称P(A)为事件A的概率

五.条件概率 乘法定理

1.条件概率

①定义

​ P(B|A)：已知事件A发生的条件下，事件B发生的概率：
$$P(B|A)=\frac{P(AB)}{P(A)}$$

②性质

​ 设P(A)>0

（1）P(B|A)>0
(2 ) P(S|A)=1
(3 ) 若事件若事件A₁,A₂,…A_n互斥,则：
$$P(A_1+A_2+...+A_n|A)=P(A_1|A)+P(A_2|A)+\cdot \cdot \cdot +P(A_n|A)$$

2.乘法定理

$$P(B|A)=\frac{P(AB)}{P(A)}\Rightarrow P(AB)=P(A)P(B|A),P(A)>0$$

$$P(A|B)=\frac{P(AB)}{P(B)}\Rightarrow P(AB)=P(B)P(A|B),P(B)>0$$

$$
P(A_1A_2A_3)=P(A_1)P(A2|A1)P(A_3|A_1A_2)

$$

$$P(A_1{A}_2...A_n)=P(A_1)P(A_2|A_1)...P(A_n|A_1{A}_2...A_{n-1})$$

六.全概率公式、贝叶斯公式

1.样本空间的划分

​ 设S为某试验的样本空间，A₁,A₂,…A_n为一组事件，满足：
（1）A₁,A₂,…A_n两两互斥
（2）A₁∪A₂∪…∪A_n=S
​ 则称A₁,A₂,…A_n为样本空间S的一个划分

2.全概率公式：

$$P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...P(A_n)P(B|A_n)$$

3.贝叶斯公式：

$$P(A_i|B)=\frac{P(A_{i}B)}{P(B)}=\frac{P(A_i)P(B|A_i)}{P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+...P(A_n)P(B|A_n)}$$

七.独立事件

1.事件独立性

①定义1（两个事件的独立性）

若两事件A、B满足：
$$P(AB)=P(A)P(B)$$
则称A与B相互独立，简称“独立”

②定义2（三个事件的独立性）

设A、B、C是三个事件，若

（1）两两独立：
$$\begin{gathered} P(AB)=P(A)P(B) \\ P(AC)=P(A)P(C) \\ P(BC)=P(B)P(C) \end{gathered}$$
（2）
$$P(ABC)=P(A)P(B)P(C)$$
则称A,B,C相互独立

2.n重贝努力试验

①定义

$$\begin{gathered} 在相同条件下可以重复试验，且任一事件出现的概率与其他各次的试验结果无关，这类试验称为n次重复独立试验 \\ 若一次试验只有A与\overline{A}两个结果，称为贝努力试验，它的n次重复独立试验，称为n重贝努力试验 \end{gathered}$$

②定理1（贝努力公式）

​ 在n重贝努力试验中，事件A发生的概率为p，则事件A恰好发生k次的概率为
$$P_n(k)=C_n^k{p}^k{q}^{n-k},q=1-p,k=0,1,...,n$$

③定理2（泊松定理）

​ 在n重贝努力试验中，事件A恰好发生k次的概率为
$$P_n(k)=C_n^k{p}^k{q}^{n-k}\approx \frac{{\lambda }^k}{k!}\cdot e^{-\lambda },\lambda =np,n\to \infty$$
重复独立试验\若一次试验只有A与\overline{A}两个结果，称为贝努力试验，它的n次重复独立试验，称为n重贝努力试验
$$

②定理1（贝努力公式）

​ 在n重贝努力试验中，事件A发生的概率为p，则事件A恰好发生k次的概率为
$$P_n(k)=C_n^k{p}^k{q}^{n-k},q=1-p,k=0,1,...,n$$

③定理2（泊松定理）

​ 在n重贝努力试验中，事件A恰好发生k次的概率为
$$P_n(k)=C_n^k{p}^k{q}^{n-k}\approx \frac{{\lambda }^k}{k!}\cdot e^{-\lambda },\lambda =np,n\to \infty$$
​ 其中，p为事件A在每次试验中出现的概率，q=1-p