Matlab 线性规划练习题
文章目录
-
-
-
- 1
- 2
- 3
- 4
- 4
-
-
1
- 问题:
数学建模某鸡场有1000只鸡,用动物饲料和谷物混合喂养。每天每只鸡平均食混合饲料0.5KG,其中动物饲料所占比例不能少于20%。动物饲料每千克0.30元,谷物饲料每千克0.18元,饲料公司每周仅保证供应谷物饲料6000KG,问饲料怎样混合,才能使成本最低?
- 解
%%
% 作业
clear; clc;
c = [0.3 0.18]; % min = 0.3*x1 + 0.18*x2
A = [-4 1]; % x1/(x1 + x2) > 0.2 化简
b = [0];
Aeq = [1 1]; % 一天的饲料量 100 * 0.5
beq = 500;
vlb = [0; 0];
vub = [ ; 6000./7]; % [0 0] <= [x1, x2] <= [+∞, 6000/7]
[x, val] = linprog(c, A, b, Aeq, beq, vlb, vub)
CONSOLE:
x =
100.0000
400.0000
val =
102.0000
2
- 问题
某工厂利用两种原料甲、乙生产 A1 、A2 、A3 三种产品 . 如果每月可供应的原料数量 (单位: t) , 每万件产品所需各种原料的数量及每万件产品的价格如下表所示:
- 试制订每月最优生产计划 , 使得总收益最大;
- 对求得的最优生产计划进行灵敏度分析
- 使用lingo求解
max = 12*x1 + 5*x2 + 4*x3;
4*x1 + 3*x2 + x3 <= 180;
2*x1 + 6*x2 + 3*x3 <= 200;
CONSOLE:
Global optimal solution found.
Objective value: 584.0000
Infeasibilities: 0.000000
Total solver iterations: 2
Variable Value Reduced Cost
X1 34.00000 0.000000
X2 0.000000 5.800000
X3 44.00000 0.000000
Row Slack or Surplus Dual Price
1 584.0000 1.000000
2 0.000000 2.800000
3 0.000000 0.4000000
3
- 问题
- 问题
每班的护士在值班开始时向病房报到 , 连续工作八个小时 . 医院领导为满足每班所需 要的护士数 , 最少需雇用多少护士 ?
- matlab求解
%%
% 5 护士值班问题
% 约束条件是 工作8个小时 2个班次刚好8个小时
clear; clc;
c = [1 1 1 1 1 1];
A = [-1 0 0 0 0 -1;
-1 -1 0 0 0 0;
0 -1 -1 0 0 0;
0 0 -1 -1 0 0;
0 0 0 -1 -1 0;
0 0 0 0 -1 -1;
];
b = [-60; -70; -60; -50; -20; -30;];
Aeq = [];
beq = [];
vlb = zeros(6, 1);
vub = [];
[x, fval] = linprog(c, A, b, Aeq, beq, vlb, vub)
CONSOLE:
x =
60
10
50
0
30
0
fval =
150
4
- 问题
某工厂生产 A1 、A2 两种型号的产品都必须经过零件装配和检验两道工序 , 如果每天 可用于零件装配的工时只有 100 h , 可用于检验的工时只有 120 h , 各型号产品每件需占用 各工序时数和可获得的利润如下表所示
- 试写出此问题的数学模型 , 并求出最优化生产方案
- 对产品 A1 的利润进行灵敏度分析
- 对装配工序的工时进行灵敏度分析
- 如果工厂试制了 A3 型产品 , 每件 A3 产品需装配工时 4 h , 检验工时 2 h , 可获利 润 5 元 , 那么该产品是否应投入生产 ?
- 使用liongo求解
model:
max = 6*x1 + 4*x2;
2*x1 + 3*x2 <= 100;
4*x1 + 2*x2 <= 120;
@gin(x1);
@gin(x2);
end
Global optimal solution found.
Objective value: 200.0000
Objective bound: 200.0000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 2
Variable Value Reduced Cost
X1 20.00000 -6.000000
X2 20.00000 -4.000000
Row Slack or Surplus Dual Price
1 200.0000 1.000000
2 0.000000 0.000000
- 用lingo求解
model:
max = 6*x1 + 4*x2 + 5*x3;
2*x1 + 3*x2 + 4*x3 <= 100;
4*x1 + 2*x2 + 2*x3 <= 120;
@gin(x1);
@gin(x2);
@gin(x3);
end
Global optimal solution found.
Objective value: 206.0000
Objective bound: 206.0000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 5
Variable Value Reduced Cost
X1 23.00000 -6.000000
X2 2.000000 -4.000000
X3 12.00000 -5.000000
Row Slack or Surplus Dual Price
1 206.0000 1.000000
2 0.000000 0.000000
3 0.000000 0.000000
4
- 问题
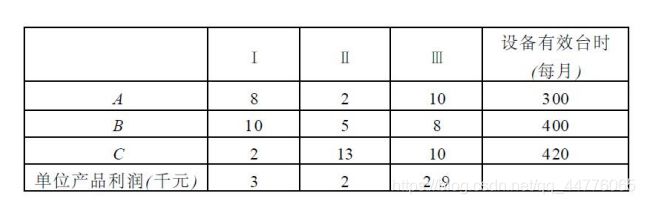
已知某工厂计划生产 Ⅰ、Ⅱ、Ⅲ 三种产品 , 各产品需要在 A、B、C 设备上加工 , 有关 数据如下
- 问题:
- 如何发挥生产能力 , 使生产盈利最大 ?
- 若为了增加产量 , 可借用别的工厂设备 B , 每月可借用 60 台时 , 租金 1 .8 万元 , 借用设备 B 是否划算
- 若另有二种新产品 Ⅳ、Ⅴ , 其中新产品 Ⅳ 需用设备 A 为 12 台时、B 为 5 台时、 C 为 10 台时 , 单位产品盈利 2 .1 千元;新产品 Ⅴ 需用设备 A 为 4 台时、B 为 4 台时、 C 为 12 台时 , 单位产品盈利 1 .87 千元 . 如 A、B、C 的设备台时不增加 , 这两种新产 品投产在经济上是否划算
- 对产品工艺重新进行设计 , 改进结构 . 改进后生产每件产品 Ⅰ 需用设备 A 为 9 台 时、设备 B 为 12 台时、设备C 为 4 台时 , 单位产品盈利 4 .5 千元 , 这时对原计划有 何影响 ?
- 使用Lingo求解
model:
max = 3*x1 + 2*x2 + 2.9*x3;
!约束条件;
8*x1 + 2*x2 + 10*x3 < 300;
10*x1 + 5*x2 + 8*x3 < 400;
2*x1 + 13*x2 + 10*x3 < 420;
x1 > 0;
x2 > 0;
x3 > 0;
@gin(x1);@gin(x2);@gin(x3); !解是整数;
end
Global optimal solution found.
Objective value: 134.5000
Objective bound: 134.5000
Infeasibilities: 0.000000
Extended solver steps: 2
Total solver iterations: 15
Variable Value Reduced Cost
X1 24.00000 -3.000000
X2 24.00000 -2.000000
X3 5.000000 -2.900000
Row Slack or Surplus Dual Price
1 134.5000 1.000000
2 10.00000 0.000000
3 0.000000 0.000000
4 10.00000 0.000000
5 24.00000 0.000000
6 24.00000 0.000000
7 5.000000 0.000000
model:
max = 3*x1 + 2*x2 + 2.9*x3 - 18;
!约束条件;
8*x1 + 2*x2 + 10*x3 <= 300;
10*x1 + 5*x2 + 8*x3 <= 460;
2*x1 + 13*x2 + 10*x3 <= 420;
@gin(x1);@gin(x2); @gin(x3);
end
Global optimal solution found.
Objective value: 127.0000
Objective bound: 127.0000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 4
Variable Value Reduced Cost
X1 31.00000 -3.000000
X2 26.00000 -2.000000
X3 0.000000 -2.900000
Row Slack or Surplus Dual Price
1 127.0000 1.000000
2 0.000000 0.000000
3 20.00000 0.000000
4 20.00000 0.000000
model:
max = 3*x1 + 2*x2 + 2.9*x3 + 2.1*x4 + 1.87*x5;
!约束;
8*x1 + 2*x2 + 10*x3 + 12*x4 + 4*x5 <= 300;
10*x1 + 5*x2 + 8*x3 + 5*x4 + 10*x5 <= 400;
2*x1 + 13*x2 + 10*x3 + 10*x4 + 12*x5 <= 420;
@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x5);
end
Global optimal solution found.
Objective value: 134.6000
Objective bound: 134.6000
Infeasibilities: 0.000000
Extended solver steps: 4
Total solver iterations: 35
Variable Value Reduced Cost
X1 24.00000 -3.000000
X2 23.00000 -2.000000
X3 5.000000 -2.900000
X4 1.000000 -2.100000
X5 0.000000 -1.870000
Row Slack or Surplus Dual Price
1 134.6000 1.000000
2 0.000000 0.000000
3 0.000000 0.000000
4 13.00000 0.000000
model:
max = 4.5*x1 + 2*x2 + 2.9*x3;
!约束条件;
9*x1 + 2*x2 + 10*x3 <= 300;
12*x1 + 5*x2 + 8*x3 <= 400;
4*x1 + 13*x2 + 10*x3 <= 420;
!整数约束;
@gin(x1);@gin(x2);@gin(x3);
end
Global optimal solution found.
Objective value: 152.8000
Objective bound: 152.8000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 8
Variable Value Reduced Cost
X1 22.00000 -4.500000
X2 24.00000 -2.000000
X3 2.000000 -2.900000
Row Slack or Surplus Dual Price
1 152.8000 1.000000
2 34.00000 0.000000
3 0.000000 0.000000
4 0.000000 0.000000