Matlab：数模11-主成分分析法

关于主成分分析法

实例

求指标对应的系数：

归一化原始数据：

方法1:

方法2:

Matlab代码（01）

%% 数据导入处理
clc
clear all
A = xlsread('/Users/fxalll/Desktop/t.xlsx','B2:K11');
%% 数据标准化处理
a = size(A,1);
b = size(A,2);
for i = 1:b
    SA(:,i) = (A(:,i) - mean(A(:,i)))/std(A(:,i));
end
%% 计算相关系数矩阵的特征值和特征向量
CM = corrcoef(SA);                          %计算相关系数矩阵
[V,D] = eig(CM);                            %计算特征值和特征向量
 
for j = 1:b
    DS(j,1)=D(b+1-j,b+1-j);                 %对特征值按降序排列
end
for i = 1:b
    DS(i,2) = DS(i,1)/sum(DS(:,1));         %贡献率
    DS(i,3) = sum(DS(1:i,1))/sum(DS(:,1));  %累计贡献率
end
 
%% 选择主成分及对应的特征向量
T = 0.9;    %主成分保留率
for K = 1:b
    if DS(K,3) >= T
        Com_num = K;
        break
    end
end
%% 提取主成分对应的特征向量
for j = 1:Com_num
    PV(:,j)=V(:,b+1-j);
end
%% 计算个评价对象的主成分的分
new_score = SA*PV;
for i = 1:a
    total_score(i,1)= sum(new_score(i,:));
    total_score(i,2)= i;
end
result_report = [new_score,total_score];    %将各主成分的分与总分放在同一个举证中
result_report = sortrows(result_report,-4); %将总分降序排列
%% 输出模型及结果报告
disp('特征值及其贡献率、累计贡献率:')
DS
disp('信息保留率T对应的主成分与特征向量:')
Com_num
PV
disp('主成分的分及排序（按第四列的总分进行降序排列，前3列为各主成分得分，第五列为企业编号）')
result_report

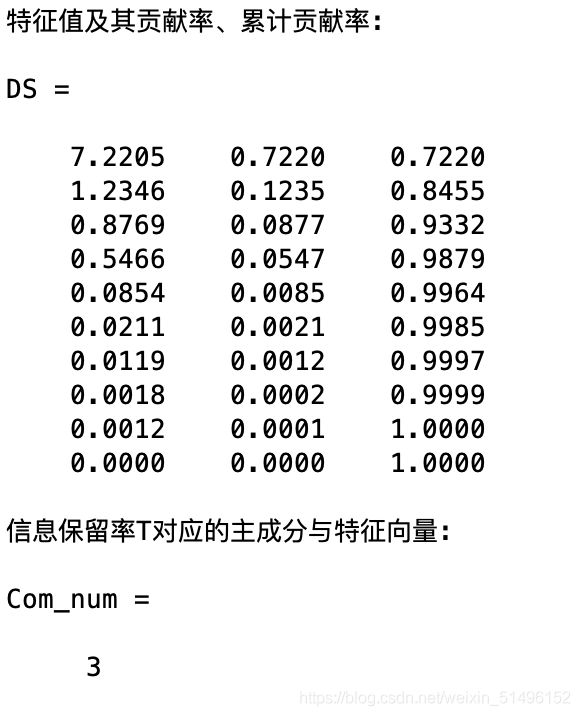
从上（result_report）可知，综合排名最高的为编号9，也就是广东。

这道题利用主成分分析法可以将原来众多具有一定相关性的变量，重新组合为一组新的相互无关的综合变量来代替原来的变量，得到综合排名。

前三个主成分为所有成分中选择累计贡献贡献率最大的三个成分。

之所以与上面的答案不同，因为这里选用了三个主成分相加进行排名，而非两个。

Matlab代码（02）

clc
clear all
%定义相关系数矩阵PHO
[X,textdata] = xlsread('/Users/fxalll/Desktop/t.xlsx');
XZ = zscore(X); %数据标准化
%主成分分析
% 调用princomp函数根据标准化后原始样本观测数据作主成分分析
%返回主成分表达式的系数矩阵COEFF，主成分得分数据SCORE
%样本相关系数矩阵的特征值向量latent和每个观测值的霍特林T2统计量
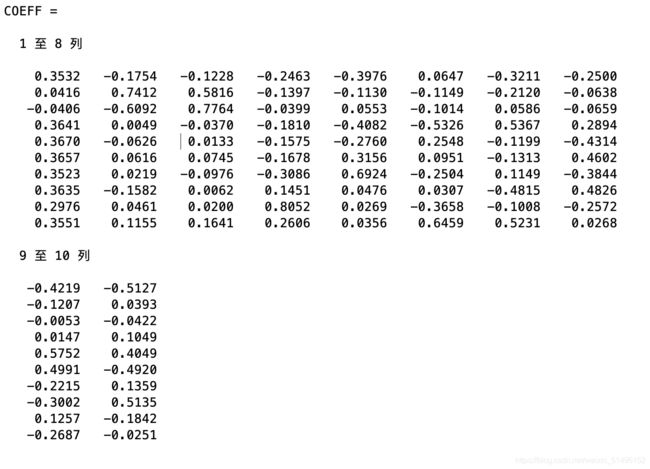
[COEFF,SCORE,latent,tsquare] = princomp(XZ)

% 为了直观，定义元胞数组result1，用来存放特征值、贡献率和累积贡献率等数据
%princomp函数不返回贡献率，需要用协方差矩阵的特征值向量latent来计算
explained = 100*latent/sum(latent);%计算贡献率

[m, n] = size(X);%求X的行数和列数
result1 = cell(n+1, 4);%定义一个n+1行、4列的元胞数组
%result1中第一行存放的数据
result1(1,:) = {
     '特征值', '差值', '贡献率', '累积贡献率'};

%result1中第1列的第2行到最后一行存放的数据(latent)特征值
result1(2:end,1) = num2cell(latent);

%result1中第2列的第2行到倒数第2行存放的数据(latent的方差，特征值的方差)
result1(2:end-1,2) = num2cell(-diff(latent));

%result1中第3列和第4列的第2行到最后一行分别存放主成分的贡献率和累积贡献率
result1(2:end,3:4) = num2cell([explained, cumsum(explained)])

% 为了直观，定义元胞数组result2，用来存放前2个主成分表达式的系数数据
varname = textdata(3,2:end)';%提取变量名数据
result2 = cell(n+1, 3); %定义一个n+1行，3列的元胞数组
result2(1,:) = {
     '标准化变量', '特征向量t1', '特征向量t2'};%result2的第一行数据
result2(2:end, 1) = varname;%result2第1列
result2(2:end, 2:end) = num2cell(COEFF(:,1:2)) %存放前2个主成表达式的系数矩阵

% 为了直观，定义元胞数组result3，用来存放每一个地区总的消费性支出，以及前2个主成分的得分数据
cityname = textdata(2:end,1);%提取地区名称数据
sumXZ = sum(XZ,2);%按行求和，提取每个地区总的消费性支出
[s1, id] = sortrows(SCORE,1);%将主成得分数据SOCRE按第一主成分得分(第一列)从小到大排序
result3 = cell(m+1, 4);%定义一个m+1行，4列的元胞数组
result3(1,:) = {
     '地区', '总支出', '第一主成分得分y1', '第二主成分得分y2'}; %第一行的数据
result3(2:end, 1) = cityname(id);%result3的第一列的数据，排序后的城市名
%result3第2列为按id排序的sumXZ，第3列为第一主成分得分y1，第4列为第二主成分得分y2
result3(2:end, 2:end) = num2cell([sumXZ(id), s1(:,1:2)])


%将主成分得分数据按得分排序
[s2, id] = sortrows(SCORE,-1);
fina_result = cell(m+1, 3);%创建一个m+1行，3列的元胞数组
%result4的第一行的数据
fina_result(1,:) = {
     '地区','第一主成分得分y1','第二主成分得分y2'};
fina_result(2:end, 1) = cityname(id);
fina_result(2:end, 2:end) = num2cell([s2(:,1:2)])