KNN-小白理解

一.KNN是什么意思？

K最近邻（k-Nearest Neighbor，KNN）分类算法可以说是最简单的机器学习算法了。所谓 K 最近邻，就是 K 个最近的邻居的意思。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。
举个例子，你的女朋友下个星期过生日，你得给她买个礼物呀，经过你的千挑万选，你看中了一个礼物，但是你又不能保证它的性价比，因此你就需要参考其他用户对于该礼物的评价了。这时候，KNN就派上用场了。

KNN算法即可以应用于分类算法中，也可以应用于回归算法中。
KNN在做回归和分类的主要区别，在于最后做预测时候的决策不同。
在分类预测时，一般采用多数表决法，其中还有加权多数表决法。
在做回归预测时，一般使用平均值法，其中还有加权平均值法。

KNN算法的优点：
1）简单、有效，分类器不需要再使用训练集进行训练，训练时间复杂度为0。
2）由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。
3）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

KNN算法缺点：
1）KNN算法是懒散学习方法（lazy learning,基本上不学习），一些积极学习的算法要快很多。
2）该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。
3）计算量较大。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

二.算法原理

如上图所示，图中的数据可以分为蓝色正方形和红色三角形两类，图中心的绿色圆点是待分类数据，下面我们通过 K 最近邻法对绿色圆点进行分类：
1.当$k=3$ 时，由图中实线圆内的数据可知：绿色圆点最近领的三个邻居中，一共有一个蓝色正方形和两个红色三角形，那么就可以将绿色圆点和红色三角形判定为一类。
2. 当$k=5$ 时，由图中虚线圆内的数据可知：绿色圆点最近领的五个邻居中，一共有三个蓝色正方形和两个红色三角形，那么就可以将绿色圆点和蓝色正方形判定为一类。
由此类推，当$k$值取值不同时,绿色圆点的分类也会不同。所以我们下面来讨论一下$k$的取值对于分类的影响。

三、k值选择

1.如果选择较小的K值，就相当于用较小的邻域中的训练实例进行预测，学习的近似误差会减小，只有与输入实例较近的训练实例才会对预测结果起作用。
缺点是学习的估计误差会增大，预测结果会对近邻的实例点分成敏感。如果邻近的实例点恰巧是噪声，预测就会出错。换句话说，K值减小就意味着整体模型变复杂，分的不清楚，就容易发生过拟合。
2.如果选择较大K值，就相当于用较大邻域中的训练实例进行预测，
其优点是可以减少学习的估计误差，但近似误差会增大，也就是对输入实例预测不准确，K值增大就意味着整体模型变的简单 。
3.注意K的取值不能是类别数的整数倍，例如你想判断一个水果是芭蕉还是香蕉，你就不能取K为2、4、6…2n。不然容易造成香蕉跟芭蕉的数目相同，导致无法判断该水果的种类。

**近似误差：**可以理解为对现有训练集的训练误差 。
**估计误差：**可以理解为对测试集的测试误差。
近似误差关注训练集，如果k值小了会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。
估计误差关注测试集，估计误差小了说明对未知数据的预测能力好。模型本身最接近最佳模型。
在实际应用中，K 值一般选择一个较小的数值，通常采用交叉验证的方法来选择最优的 K 值。随着训练实例数目趋向于无穷和 K=1 时，误差率不会超过贝叶斯误差率的 2 倍，如果 K 也趋向于无穷，则误差率趋向于贝叶斯误差率。（贝叶斯误差可以理解为最小误差）

三种交叉验证方法：
Hold-Out： 随机从最初的样本中选出部分，形成交叉验证数据，而剩余的就当做训练数据。 一般来说，少于原本样本三分之一的数据被选做验证数据。常识来说，Holdout 验证并非一种交叉验证，因为数据并没有交叉使用。

K-foldcross-validation：K 折交叉验证，初始采样分割成 K 个子样本，一个单独的子样本被保留作为验证模型的数据，其他 K-1 个样本用来训练。交叉验证重复 K 次，每个子样本验证一次，平均 K 次的结果或者使用其它结合方式，最终得到一个单一估测。这个方法的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次，10 折交叉验证是最常用的。

Leave-One-Out Cross Validation：正如名称所建议， 留一验证 (LOOCV) 意指只使用原本样本中的一项来当做验证资料， 而剩余的则留下来当做训练资料。 这个步骤一直持续到每个样本都被当做一次验证资料。 事实上，这等同于 K-fold 交叉验证是一样的，其中 K 为原本样本个数。(以上三种方法转自姜佬的博客)

四.算法步骤

1）初始化：初始化数据集。
2）算距离：给定测试对象，计算它与训练集中的每个对象的距离。
3）找邻居：圈定距离最近的k个训练对象，作为测试对象的近邻。
4）做分类：根据这k个近邻归属的主要类别，来对测试对象分类。

1.初始化数据集
初始化训练集和测试集。
训练集一般为两类或者多种类别的数据。
测试集一般为一个数据。

2.计算距离
计算距离的公式非常多。这里我介绍比较简单的几种。
闵氏距离
设n维空间中有两点坐标x, y，p为常数，闵式距离定义为
$$D(x,y)=(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}$$
注意：
（1）闵氏距离与特征参数的量纲有关，有不同量纲的特征参数的闵氏距离常常是无意义的。
（2）闵氏距离没有考虑特征参数间的相关性，而马哈拉诺比斯距离解决了这个问题。绝对距离

当p=1时，得到绝对值距离，也叫曼哈顿距离（Manhattan distance）、出租汽车距离或街区距离（city block distance）。在二维空间中可以看出，这种距离是计算两点之间的直角边距离，相当于城市中出租汽车沿城市街道拐直角前进而不能走两点连接间的最短距离。(顾名思义，城市街区的距离就不能是点和点的直线距离，而是街区的距离）。
如棋盘上也会使用曼哈顿距离的计算方法：
定义如下：
$$d=\sqrt{\sum _{i=1}^n|x_i-y_i|}$$

欧氏距离
当p=2时，得到欧几里德距离（Euclidean distance）距离，就是两点之间的直线距离（以下简称欧氏距离）。
定义如下：
$$d=\sqrt{\sum _{i=1}^n(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$

切比雪夫距离
令$p\to \infty$，得到切比雪夫距离。切比雪夫距离

3.寻找最近邻数据
将所有距离进行升序排序，确定 K 值，最近的 K 个邻居即距离最短的 K 个数据。

4.决策分类
明确 K 个邻居中所有数据类别的个数，将测试数据划分给个数最多的那一类。即由输入实例的 K 个最临近的训练实例中的多数类决定输入实例的类别。
最常用的两种决策规则：
多数表决法：多数表决法和我们日常生活中的投票表决是一样的，少数服从多数，是最常用的一种方法。
加权表决法：有些情况下会使用到加权表决法，比如投票的时候裁判投票的权重更大，而一般人的权重较小。所以在数据之间有权重的情况下，一般采用加权表决法。

如下图所示(其中K=4)：

四.代码实现

import matplotlib.pyplot as plt#便于书写
import matplotlib#引进绘图库
from math import sqrt#引进平方根
##### 初始化数据集 #####
data_A = [[1,2],[3.2,4],[4,7],[5.2,3],[7,4.1]]#数据集 A
data_B = [[2.2,5.5],[4.2,2],[5,5],[6.3,7]]#数据集 B
test_data = [[4.5,4.5]]#测试集
len_A = len(data_A)#计算长度方便遍历循环
len_B = len(data_B)#同理


##### 计算距离并排序 #####
distance_A = []#与 A 类数据之间的距离
distance_B = []#与 B 类数据之间的距离
distance = []#全部距离
#计算距离（使用欧氏距离）
for i in range(len_A):    
    d = sqrt((test_data[0][0]-data_A[i][0])**2+(test_data[0][1]-data_A[i][1])**2)#套公式，前面为x，后面为y
    distance_A.append(d)
    for i in range(len_B):    
        d = sqrt((test_data[0][0]-data_B[i][0])**2+(test_data[0][1]-data_B[i][1])**2)#同理 
        distance_B.append(d)
#由小到大排序（此处使用冒泡排序），很经典的一个算法
distance = distance_A + distance_B
for i in range(len(distance)-1):    
	for j in range(len(distance)-i-1):        
		if distance[j] > distance[j+1]:    #判断前后数据大小，如果前面大于后面，就相互交换        
			distance[j],distance[j+1]=distance[j+1],distance[j]
print("距离所有A类数据的距离为："）
print(distance_A)
print()#打印一行空白，即换行
print("距离所有B类数据的距离为：")
print(distance_B)
print()#同理
print("对所有的距离升序排序：")
print(distance)
print()#同理


##### 按 K 最近邻对测试集进行分类 #####
K = 5#这里默认 K 值为 5，也可以自行更改
number_A = 0
number_B = 0
#定义删除函数，避免对同一个数据重复计算
def delete(a,b,ls):    
    for i in range(b):        
        if ls[i]==a:            
            ls.pop(i)     #如果判断出第i个数据为a，就把第i个数据删除
     	    break
        #找出与测试数据最接近的 K 个点
        for i in range(K):    
            if distance[i] in distance_A:      #判断小的距离值是否在A中  
                number_A += 1        #计数器
                delete(distance[i],len(distance_A),distance_A)        
                continue    #退出当前循环，如果这里分不清continue和break的作用，我专门写了一篇博客[continue与break区别](https://blog.csdn.net/hcxddd/article/details/116357148)
            if distance[i] in distance_B:      #判断小的距离值是否在B中
                number_B += 1        #计数器
                delete(distance[i],len(distance_B),distance_B)        
                continue	#退出当前循环
            print("最终结果：")
            print("距离待测数据最近的K={:}个数据中，A类数据有{:}个，B类数据有{:}个".format(K,number_A,number_B))
            if number_A > number_B:   #对A类，B类的数值大小进行判断 
                print("所以K={:}时，待测数据划分为A类".format(K))
            else:    
                print("所以K={:}时，待测数据划分为B类".format(K))




##### 画图 #####
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
for i in range(len_A):#A 类，用红色三角形表示    
    if i!=len_A-1:        
        plt.plot(data_A[i][0],data_A[i][1],'bo',marker='^',color='red')    
    else:        
        plt.plot(data_A[i][0],data_A[i][1],'bo',marker='^',label='A',color='r')    
        #使用 if..else... 是为了避免在图形中重复出现多个标签
        for i in range(len_B):#B 类，用蓝色正方形表示    
            if i!=len_B-1:        
                plt.plot(data_B[i][0],data_B[i][1],'bo',marker='s',color='blue')    
            else:        
                plt.plot(data_B[i][0],data_B[i][1],'bo',marker='s',label='B',color='b')
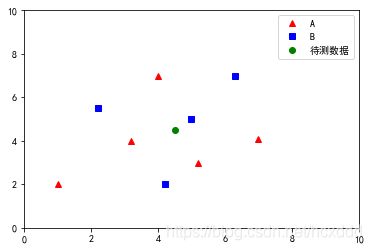
                plt.plot(test_data[0][0],test_data[0][1],'bo',label='待测数据',color='g')#测试集
                plt.xlim(0,10)
                plt.ylim(0,10)
                plt.legend()
                plt.show()
              

距离所有A类数据的距离为：
[4.301162633521313, 1.3928388277184118, 2.5495097567963922, 1.6552945357246849, 2.5317977802344327]

距离所有B类数据的距离为：
[2.5079872407968904, 2.5179356624028344, 0.7071067811865476, 3.080584360149872, 2.5079872407968904, 2.5179356624028344, 0.7071067811865476, 3.080584360149872, 2.5079872407968904, 2.5179356624028344, 0.7071067811865476, 3.080584360149872, 2.5079872407968904, 2.5179356624028344, 0.7071067811865476, 3.080584360149872, 2.5079872407968904, 2.5179356624028344, 0.7071067811865476, 3.080584360149872]

对所有的距离升序排序：
[0.7071067811865476, 0.7071067811865476, 0.7071067811865476, 0.7071067811865476, 0.7071067811865476, 1.3928388277184118, 1.6552945357246849, 2.5079872407968904, 2.5079872407968904, 2.5079872407968904, 2.5079872407968904, 2.5079872407968904, 2.5179356624028344, 2.5179356624028344, 2.5179356624028344, 2.5179356624028344, 2.5179356624028344, 2.5317977802344327, 2.5495097567963922, 3.080584360149872, 3.080584360149872, 3.080584360149872, 3.080584360149872, 3.080584360149872, 4.301162633521313]

绘制图像如下：

最终我们可以判断出：
离待测数据最近的K=5个点中，有2个属于类型A，3个属于类型B。
此我们把绿色原点归为类型B。