当自变量和因变量成强相关性时,我们优先考虑线性相关。
python的sklearn有现成的库去计算线性回归中的参数,我们需要做的就是调库。。。#江湖人称“调包侠”
Case 1 一维变量
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_Model import LinearRegression
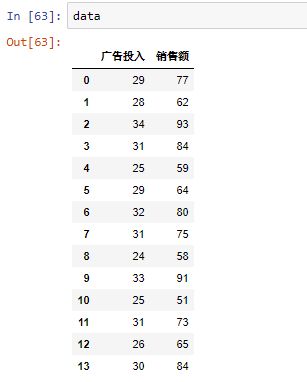
- 开始导入数据
data=pd.read_csv('C:\\PDM\\4.1\\data.csv')
data
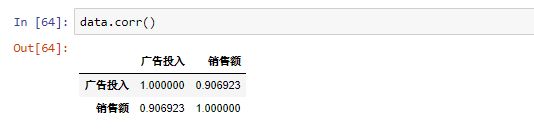
- 查看相关性
data.corr()
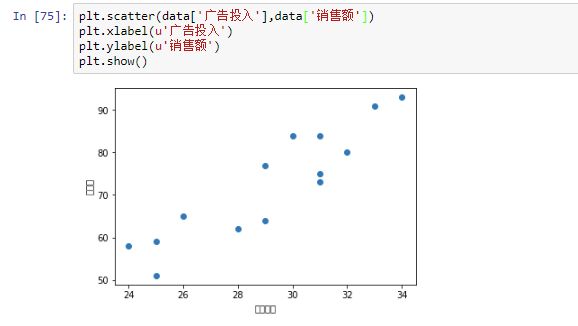
-
散点图查看分布
- 开始调包计算
from sklearn.linear_model import LinearRegression
IrModel = LinearRegression()
IrModel.fit(data[['广告投入']], data[['销售额']])
theta0=IrModel.intercept_[0]
theta1=IrModel.coef_[0]
xx=np.linspace(min(data['广告投入']),max(data['广告投入']),10)
yy=theta0+theta1*xx
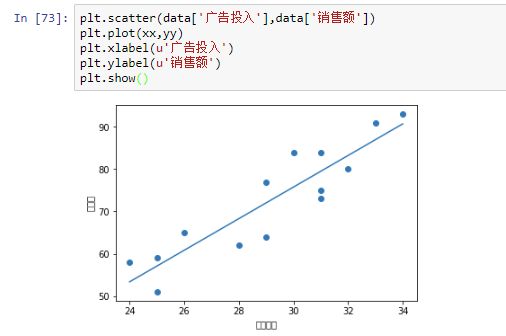
-
查看拟合结果
-
查看拟合评分
-
进行预测
- 预测广告投入分别为50,40,30情况时的销售额情况。
Case 2 多维变量
y=\theta_0+\theta_1*x_1+\theta_2*x_2
- 同上调包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
- 导入数据
data=pd.read_csv('PDM\\xx\\4.2\\data.csv')
data
-
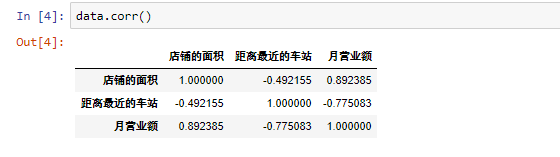
查看相关性
在这里,“月营业额”作为目标变量(待预测变量),“店铺面积”,“距离最近的车站”作为因变量,通过相关性分析,我们发现,店铺面积和月营业额成正相关,距离最近的车站和月营业额成负相关。
- 进行拟合
IrModel=LinearRegression()
IrModel.fit(data[['店铺的面积','距离最近的车站']],data[['月营业额']])
IrModel.score(data[['店铺的面积','距离最近的车站']],data[['月营业额']])
分数还是蛮高的
-
进行预测
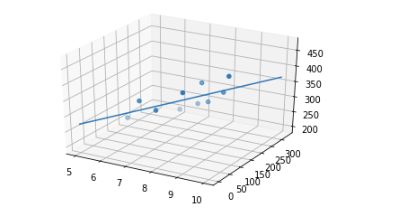
- 可视化
theta0=IrModel.intercept_[0]
theta1=IrModel.coef_[0,0]
theta2=IrModel.coef_[0,1]
x=np.linspace(min(data['店铺的面积']),max(data['店铺的面积']),20)
y=np.linspace(min(data['距离最近的车站']),max(data['距离最近的车站']),20)
z=theta0+theta1*x+theta2*y
from mpl_toolkits.mplot3d import Axes3D
ax = plt.figure().add_subplot(111, projection = '3d')
ax.scatter(data[['店铺的面积']],data[['距离最近的车站']],data[['月营业额']])
ax.plot(x,y,z)
plt.show()
目前的工作主要是回归,后面涉及到的分类,就是分隔超平面了。