Codeforces Round #719 (Div. 3) A - E 题解

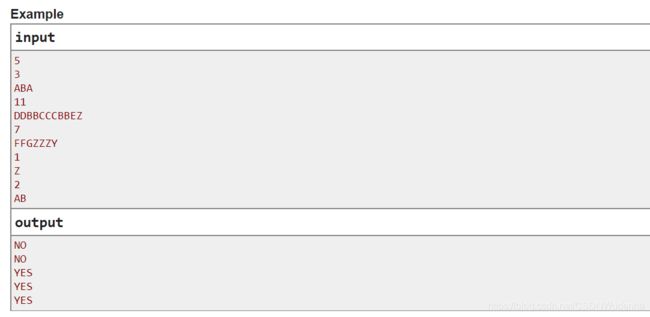
A. Do Not Be Distracted!

原题链接:https://codeforces.ml/contest/1520/problem/A

题目大意

如果诸如AAAADDBBFGH 这样, 每一个字母只连续出现 1 次, 那么输出 YES, 否则像 AABBA这样 A 在不同的位置连续出现 2 次及以上则输出 NO.

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 100;
char str[N]; 

int main() {
     
	//freopen("D:\\in.txt", "r", stdin); 
	//freopen("D:\\out.txt", "w", stdout);
	rit;
	while (t --) {
     
		rin;
		getchar();
		sc("%s", str);
		getchar();
		int book[26] = {
     0};
		bool flag = true;  //flag为false表示连续出现2次及以上
		for (int i = 0; i < n; ++ i) {
     
			int a = str[i] - 'A';
			int j = i + 1;
			while (j < n && str[j] == str[i]) ++ j;  //跳过连续相同的部分
			i = j - 1;
			if (book[a]) {
     
				flag = false;
				break;
			}
			++ book[a];
		}
		if (flag) pr("YES\n");
		else pr("NO\n");
	} 
	return 0;
}

B. Ordinary Numbers

原题链接:https://codeforces.ml/contest/1520/problem/B

题目大意

如果一个数字各个位上的数字是一致的,那么称之为普通数, 如 1, 99, 111等等.
请计算从 1 到 n 之间有多少个普通数.

思路

很显然, 所有一位数一共有 9 个普通数, 所有两位数也是一共有 9 个普通数, 所有三位数也是一共只有 9 个普通数.

那么对于一个数 9876 , 我们可以先获得出这是一个 四位数, 那么对于一位、二位、三位数, 就已经可以有 3 * 9 = 27 个普通数了.
而由于 9876 的最高位是 9 , 那么所有四位数里, 至少会有 9 - 1个普通数, 而又由于 9876 < 9999, 所以不需要再加一.
综上, 1 到 9876 之间的普通数一共有 27 + 8 个.

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 10000; 

//获得 n 的位数
int dswei(int n) {
     
	int ans = 0;
	while (n > 0) {
     
		++ ans;
		n /= 10;
	}
	return ans;
}

//获得 n 的最高位数字,其中 n 是一共 a 位的数字
int zgwei(int n, int a) {
     
	return n / (int)(pow(10, a - 1));
}

//获得由a个b构成的数
int hdzhi(int b, int a) {
     
	int ans = 0;
	while (a --) {
     
		ans = ans * 10 + b;
	}
	return ans;
}

int main() {
     
	//freopen("D:\\in.txt", "r", stdin); 
	//freopen("D:\\out.txt", "w", stdout);
	rit;
	while (t --) {
     
		rin;
		int a = dswei(n);
		int ans = (a - 1) * 9;
		int b = zgwei(n, a);
		ans += b - 1;
		if (n >= hdzhi(b, a)) ans ++;
		pr("%d\n", ans);
	}
	return 0;
}

C. Not Adjacent Matrix (构造相邻位置数值不相邻矩阵)

原题链接:https://codeforces.ml/contest/1520/problem/C

题目大意

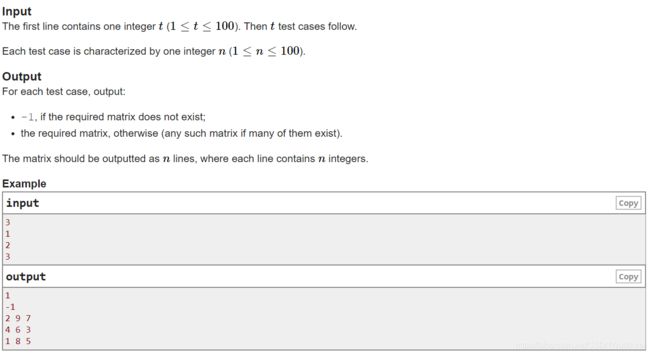
构造一个 n * n 的矩阵, 其中矩阵每一位的数字都在 1 到 n * n 的范围内, 且每个数字只能用一次.
同时, 矩阵中每个数字与其上下左右的数的绝对值必须大于 1.
如果这样的矩阵构造不出来, 则输出 -1, 否则输出矩阵.

思路

显然, 数值相邻的数字不能放在相邻的两格, 这道题应该是有多种填充方法的, 这里我主要是斜着填充, 最后在更改一下 2 和 n * n 的位置即可. 具体如下图 :

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 110; 

int ans[N][N];


int main() {
     
	//freopen("D:\\in.txt", "r", stdin); 
	//freopen("D:\\out.txt", "w", stdout);
	rit;
	while (t --) {
     
		rin;
		if (n == 1) pr("1\n");
		else if (n == 2) pr("-1\n");  //除了2不可以,其余都能构造矩阵
		else {
     
			int cnt = 1;  //填充数字的计数器
			//填充 1 到对角线的数字
			for (int i = n; i >= 1; -- i) {
     
				int x = i, y = 1;
				while (x >= 1 && x <= n && y >= 1 && y <= n) {
     
					ans[x][y] = cnt ++;
					++ x;
					++ y;
				}
			}
			//填充对角线到 n * n
			for (int i = 2; i <= n; ++ i) {
     
				int x = 1, y = i;
				while (x >= 1 && x <= n && y >= 1 && y <= n) {
     
					ans[x][y] = cnt ++;
					++ x;
					++ y;
				}
			}
			//输出矩阵
			for (int i = 1; i <= n; ++ i) {
     
				for (int j = 1; j <= n; ++ j) {
     
					if (ans[i][j] == 2) pr("%d", n * n);
					else if (ans[i][j] == n * n) pr("%d", 2);
					else pr("%d", ans[i][j]);
					if (j < n) pr(" ");
				}
				pr("\n");
			}
		}
	}
	return 0;
}

D. Same Differences (序列求数对数量)

原题链接:https://codeforces.ml/contest/1520/problem/D

题目大意

对于一个有 n 个数的序列, 找到满足 i < j 且 aj − ai = j − i 的两个数ai 和 aj, 并输出该序列一共有多少对这样的 ai 和 aj.

思路

假如有一个序列为 1, 6, 3, 4, 5, 7
那么很显然, 这个序列里面只有 1, x, 3, 4, 5, x 这其中的 4 个数彼此之间可以构成满足题目要求的对子.
而 x, 6, x, x, x, x 和 x, x, x, x, x, 7 都各自无法与其他数构成对子.

这里我们就可以在抽象出来, 在原序列队头增加一个计数器 ( 计数器可由哈希表实现, 也可以数组模拟, 因为题目数值有限定一定小于等于 n ) , 该计数器的意义在于计算要想和 6 能构成对子的起始值序列.
比如说 [计数器 + 1, 6, 3, 4, 5, 7], 而 1, x, 3, 4, 5, x 在计数器表示值为 0, 因为是以 0 为起始才能保证严格单调递增, 而当遇到 1 时, ans += map[ 0 ] , map[ 0 ] ++; 当遇到 3 , 则 ans += map [0] , map [ 0 ] ++ ……

这里 ans += map [0] 表示因为 3 索引为 3, 那么必须是同样处于队头 0 的数字才能和 3 构成合法对子;
map [ 0 ] ++ 表示以 0 为队头的队伍新加入一员, 往后能和队头为 0 的数组队的数又多了一个.

语言可能表述的没有很好, 但是只要照着代码自己手动模拟一遍应该就能明白.

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 200010; 

int main() {
     
	//freopen("D:\\in.txt", "r", stdin); 
	//freopen("D:\\out.txt", "w", stdout);
	rit;
	while (t --) {
     
		rin;
		ll ans = 0;
		unordered_map<int, int> m;
		for (int i = 1; i <= n; ++ i) {
     
			ria;
			ans += m[a - i];
			++ m[a - i];
		}
		pr("%lld\n", ans);
	}
	return 0;
}

E. Arranging The Sheep (贪心: 求最少操作数)

原题链接: https://codeforces.ml/contest/1520/problem/E

题目大意

假如有这么一串字符串 * . * . . . * . * * , * 代表绵羊, . 代表空位, 现在要求在最少操作次数下, 使得所有绵羊聚集在一起(彼此之间没有空位), 至于是 聚集成 * * * * * . . . . . 还是 . . . * * * * * . . 又或者其他形式都可以.

思路

当处于位置 idx 时, 我们用 L 表示在 idx 左边有多少只绵羊, 用 R 表示在 idx 有多少只绵羊.

那么对于 idx , 假如这个位置本身有 绵羊, 那么 ++ L, – R
如果这个位置为空, 那么此时哪一边绵羊数量少, 就让哪一边的绵羊往这个位置的反向移动一步 .

(
这里其实, L 代表的是此时 idx 的左边已经有多少个聚成团了, 如果 ans += L, 代表左边这个团体整体向右移动一步;

而 R 其实代表的是, 在 idx 的右边还有多少个可能还没聚成团, 而 ans += R, 那么这条语句代表的是, 如果让左边已经聚成团的整体集体向右移动是很亏的, 倒不如让右边可能还散着的绵羊在原来的位置上向左移动一步, 毕竟只要最后它们都聚在一起即可, 停在哪个区间并不重要
)

比如对于序列 * . * . . . * . * * 整个过程如下 :

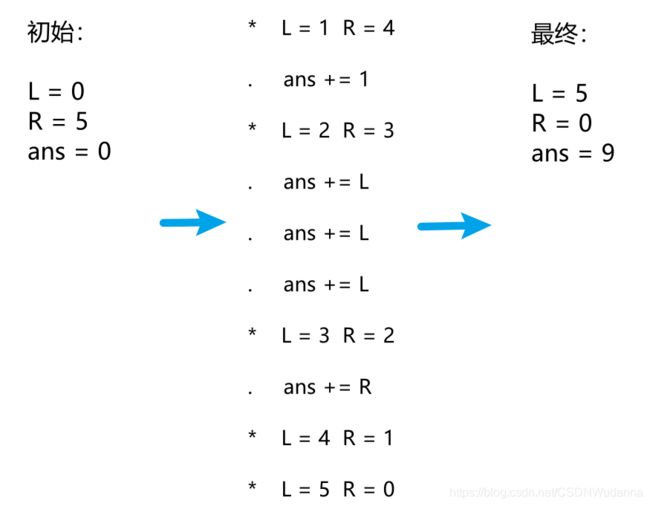
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

#define getlen(array) {return (sizeof(array) / sizeof(array[0]));}
#define ll long long 
#define ull unsigned long long
#define PII pair
#define MEM(x, y) memset(x, y, sizeof x)
#define rin int n; scanf("%d", &n)
#define rln ll n; scanf("%lld", &n)
#define rit int t; scanf("%d", &t)
#define ria int a; scanf("%d", &a)
#define sc scanf
#define pr printf

const int INF = 0x3f3f3f3f;
const int N = 1000010;

char str[N]; 

int main() {
     
	freopen("D:\\in.txt", "r", stdin); 
	//freopen("D:\\out.txt", "w", stdout);
	rit;
	while (t --) {
     
		rin;
		getchar();
		sc("%s", str);
		ll ans = 0;
		int l = 0, r = 0;
		// 计算绵羊数目
		for (int i = 0; i < n; ++ i) {
     
			if (str[i] == '*')
				++ r;	
		}
		for (int i = 0; i < n; ++ i) {
     
			if (str[i] == '*') {
     
				++ l;
				-- r;
			}
			else {
     
				ans += min(l, r);
			}
		}
		pr("%lld\n", ans);
	}
	return 0;
}