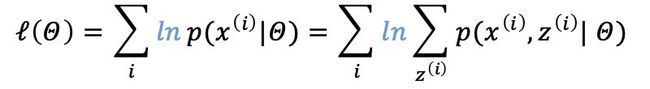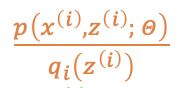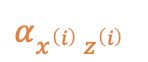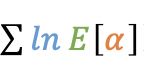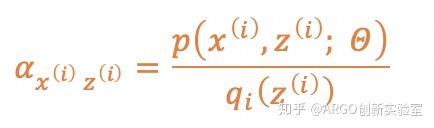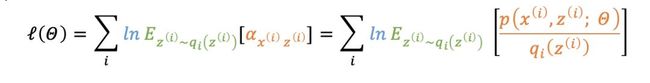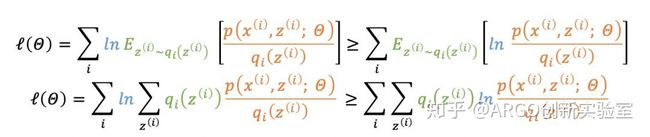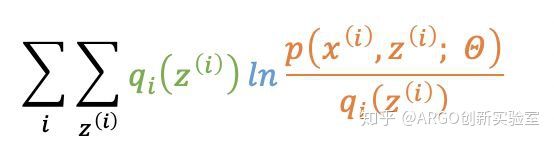kmeans聚类算法_EM算法简介
作者:bobo
EM算法是机器学习十大算法之一, 在机器学习史上提出极早,影响范围极广。本文由浅入深,逐步推导EM算法,使读者更深刻的理解EM算法。
本文从EM算法的基本概念说起,提出对于EM算法的一些基本认知问题,而后通过抛硬币实例让读者更好的理解EM算法和理解这个算法要去解决的实际问题,全文主要分为如下几个部分:
- 初识EM算法
- 从抛硬币说起 - 极大似然估计与隐变量
- 似曾相识的模式 - K-Means
- 推导接近EM的优化算法
- 问题和算法的形式化
- 应用和推广
一 初识EM算法
EM算法全称Expectation Maximization算法,即期望最大化算法。EM算法是机器学习十大方法之一, 由Arthur P. Dempster,Nan Laird和Donald Rubin 1977年正式提出,是一种在已知部分相关变量的情况下,估计未知变量的迭代算法,该算法之前已经在许多特定的领域中被应用。
三位作者从左至右Arthur P. Dempster,Nan Laird和Donald Rubin
EM的算法流程相对而言比较简单,其步骤如下:
step1 :初始化分布参数
step2 :重复E、M步骤直到收敛:
a) E步骤-期望值计算:根据参数的假设值,给出未知变量的期望估计,应用于缺失值。
b) M步骤-最大化计算:根据未知变量的估计值,给出当前的参数的极大似然估计。
EM算法的描述看似非常直白简单,然而真正理解它的算法设计、有效性和实际应用,还需要思考这些问题:
- 这个算法要解决什么样的问题?
- 已知部分相关变量指的是什么,未知变量是哪些?
- 求解过程中为什么需要进行迭代?
- 迭代过程的关键是什么?
- 从数学的角度来看,EM算法是如何推演的?
本文将注重EM算法基本概念的理解,从最简单的抛硬币实验开始,并通过逐步的改进重现EM算法的构造过程, 最后对EM算法的数学推导中关键步骤进行辅助说明和解释,希望初次接触EM算法的读者们有更深刻的了解。
二 从抛硬币说起- 极大似然估计与隐变量
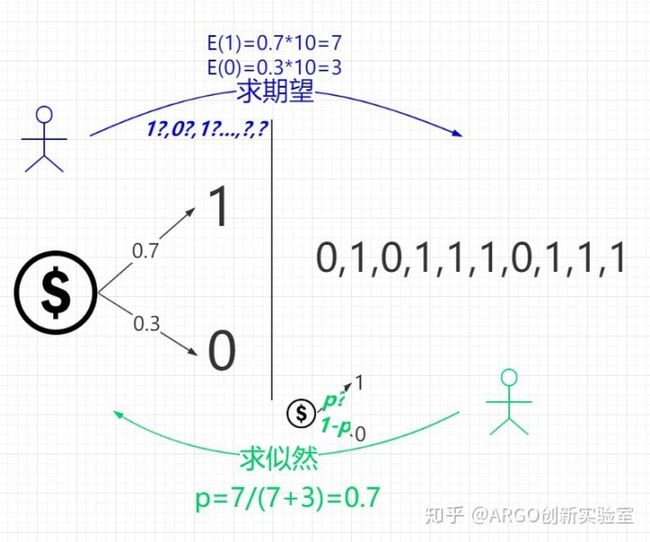
在重复抛硬币实验中,如果知道硬币抛出正面的概率p,就可以计算n次试验结果中抛出正面的期望
对于上图中的两个不同颜色的小人,我们按照颜色姑且称之为小蓝和小绿。这两个小伙伴相处得很和谐:
- 小蓝知道硬币的正反面概率分布,根据该分布可以计算出实验结果序列的期望E。如上图所示,如果硬币正面概率是0.7,意味着能够计算出每种不同的序列的概率,从而得到总体概率最大的序列结果。
- 小绿知道实际的试验结果,可以对硬币的分布进行极大似然估计。比如,如上图所示,小绿所估算出的p=0.7。p表示在当前的观察结果下,硬币抛出正面的概率,最可能的参数是0.7。
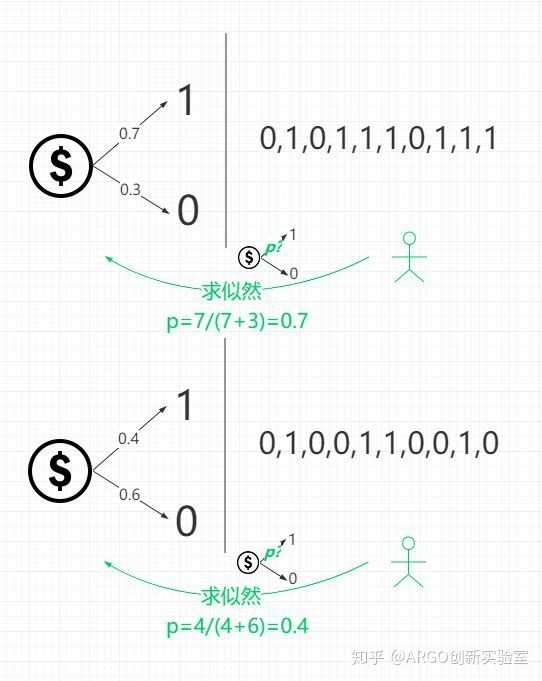
对于小绿来说,掌握了方法后,对多枚硬币分别进行估计和一枚硬币进行估计并没有区别,在逐渐复杂的参数估计任务下,小绿开始了打怪升级的过程。第二层任务这种情况如下图所示:
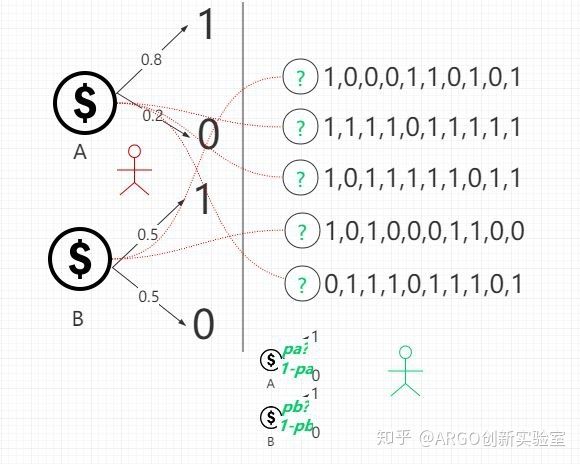
事物是发展的,小绿在掌握了这种技能不久之后,就遇到了一个比较头疼的问题,要估计的问题形式上发生了变化:一次猜测多个硬币的投掷概率,但试验结果和具体硬币的关系被隐藏了。在多个硬币的实验中,不仅不知道每个硬币的投掷结果概率分布,并且还不知道每个实验结果分别是来自于哪个硬币的话,小绿还有办法估算出硬币的分布吗?如下图,小红从两枚硬币中选择一枚重复抛十次,小绿只能看到每组试验的结果,却不知道小红每次使用的硬币是哪个:
此时小绿要如何估计出这两枚硬币的投掷结果概率参数呢?更进一步地,有没有办法估计出每次使用的硬币是哪一枚呢?此时,由于每次使用的硬币不可观察,实质上引入了一个额外的未知量,简单的似然估计已经不再适用了。这个引入的未知量叫做隐变量(Latent (hidden/unobserved) variable),而EM算法正是解决这类含隐变量问题的一种通用方法。
三 似曾相识的模式:K-Means
学习了解过K-Means的同学相信已经感受到了这个问题的模式有些熟悉的味道,回顾一下ARGO之前介绍过的KMeans聚类中的问题,输入只有样本本身和类数量K,未知的信息包括:
1. 每个类的分布及其中心点
2. 每个样本点所属的类别
这正好和小绿当前在抛硬币实验中的困境对应上了:
在KMeans方法中,解决问题的方法采用了迭代的思想,随机选取初始值,通过不断地迭代,分别更新集群的中心和样本的类别, 在每个迭代循环中:
- 以所估计的类别中心为基础,对每个计算样本分别和所有类别中心的距离,选取距离最小的作为其所属类别
- 以上一步中每个类别里的所分配样本为基础,重新计算类别的中心
此处,迭代分为两个步骤,分别对应两个未知量:每次只更新一个估计值,另一个未知量的估计值则被视为当前步骤中的已知量,最终达到聚类的目的,并估计出每个类别的分布和样本于类别的对应关系。
并且这两个问题还有一个重要的共同点,就是两个未知量之间是互相关联的,获得其中任意一个,就可以对另一个值进行估计。提高其一个值的准确度后,也可以对另一个值进行更新,提高其准确度。那么KMeans的思路可以用来解决这个问题吗?对此,小绿同学进行了一些尝试。
四 推导接近EM的优化算法
小绿同学算法分为1.0和2.0两个版本对该小红一顿瞎扔制造的难题进行了尝试:
a) 小绿算法1.0: 迭代,分步计算未知量
借鉴KMeans算法的思想,小绿构造出这样一个迭代算法,我们称之为小绿算法1.0:
1 设定各个硬币的参数的初始估计值
2 E步:模仿KMeans,在第
3 M步:根据2的结果,重新统计各组试验结果的分布,分别更新对应的硬币投掷结果概率分布,作为下一轮的迭代假定参数。例如,假设估计出实验中的第1,2,3组(分别有5,9,8个正面)来自硬币A,则更新A的分布参数为(5+8+9)/30~=0.733,从而得到下一轮的迭代参数
4 当硬币参数的估计值变化范围很小时,停止迭代,所得到的值就是对每个硬币的参数的估计,同时也得到了每次实验对应的硬币的估计。
小绿用这个方法一试,迭代很快结束了,预测结果看上去非常粗糙:
- 设定初始值
- 第一轮迭代,得到
第二轮迭代,得到,参数没有更新,迭代结束
由于两个估计值都没有更新,小绿经过两轮迭代就结束了,对照小红的选择和硬币的真实分布参数,在这个例子中貌似可以得到接近真实的估计值。然而这个算法真的可以通用地解决这一类的问题吗?
小绿和小红经过反复的验证发现,无论初始的参数是如何选取的,迭代的次数依旧不高。那有没有办法对这个算法进行改进呢?小绿经过思考,发现了算法中有一个地方是可以改进的 – 在算法E步中,只选取了一枚硬币。世界并非非黑即白,为什么不来个折中呢,要微调,要提高准确度和迭代次数!
b)小绿算法2.0: Hard –> Soft
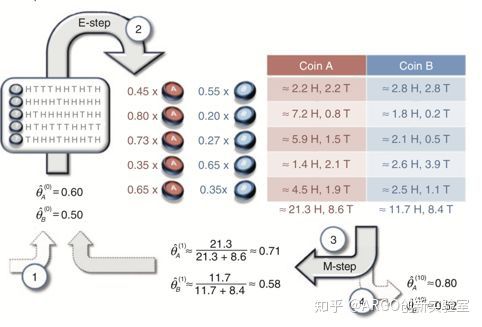
在小绿算法1.0中,为什么只能选取一枚硬币呢,其实我们可以同时取两枚硬币,所有的结果都可以认为是两枚硬币的共同作用导致的。这样,可以同时计算两枚硬币对应的概率分配样本,同时更新权重。按照这样的思路即可优化出小绿算法2.0:
1 设定各个硬币的参数的初始估计值
2 在第
,据此计算出每组结果序列分别使用这两枚硬币产生该序列的概率
3 在第
4 当硬币参数的估计值变化范围很小时,停止迭代,所得到的值就是对每个硬币的参数的估计。
经过反复的试验,小绿发现2.0的算法相比于1.0效果更好了-这个版本可以多轮反复地迭代并不断逼近真实的参数:
图片来自http://ai.stanford.edu/~chuongdo/papers/em_tutorial.pdf
相比于1.0的算法,2.0算法改进的重要一点在于,每次计算样本和分类的从属关系时,不是采用Hard的0-1判定方法,而是采用权重化的Soft分配,即从非0即1的选择(每组数据只用于更新一个硬币的分布)进化,使得所有的硬币在所有的实验组中都得到了用于更新参数的数据。
至此为止,小绿2.0已经具备了EM算法的结构,两个版本正体现了EM算法中的关键:
- 通过迭代逐步优化估计值,并且在迭代过程中,每个步骤只优化/计算一个未知量(硬币的参数或者实验结果对应的硬币),视其他未知量(的估计值)为已知量。
- 迭代过程中,使隐变量的所有可能的取值都参与计算(Hard->Soft)。
至此,EM算法解决的问题和构造的思路已经基本介绍完毕。根据上文的思路,我们可以构造出更多类似的问题,只要将隐变量这个概念引入基本的似然估计过程,就会导致问题无法直接求解而需要用EM算法的方式来求解。
举例:
- 男女生的身高问题:假设男女生升高分别服从不同参数的正态分布,如何根据一组身高样本估计出:1)某样本是来自男生还是来自女生?2)男女生各自的分布参数分别是什么?
- 买水问题:假设多名顾客经常到某小卖部消费,每次购买矿泉水的概率服从不同参数伯努利分布,如何根据一组账单估计出:1)该账单对应的是哪位顾客?2)每个顾客买矿泉水的概率是多大?
五 问题和算法的形式化
上述例子虽然表述多样,然而在数学上的问题是一致的,对问题的形式化描述如下:
模型
其中
由于
Jensen不等式
Jensen 不等式(Jensen’s ineuiality) 体现了凸函数(Convex Function)的特性:
对于一组x的集合,有
其中等号成立的条件是中x集合的所有元素相等。不等式的描述如下图所示:
图片来自https://people.duke.edu/~ccc14/sta-663/EMAlgorithm.html
EM算法的推导
1)求解模型参数最优解
对函数
一般而言,需要求极值问题,可以转化为求导数为0的点是最简单的。但由于上式右边存在隐变量z,z是x的未知函数,从而使得该函数无法求导,简单的MLE无法直接解决,这也是为什么EM算法通过迭代求解问题的原因。
这里,需要求参数
记
为
(简写为
(简写为
(即
上式也可理解为
代入
有
由于ln函数是一个凹函数,根据Jensen不等式
有,
其中
为log似然函数的下界,从而得到:
上式中等号成立的条件是(Jensen不等式等号成立的条件):
其中c是一个常数。
由于
满足
,可得:
其中,
综合上述,求解模型参数的问题:
2) 算法具体步骤
根据上面的推导,即可得到EM算法的步骤:
在迭代的第t轮循环中,当前的参数估计为
E步(固定
即在给定观测序列和估计的模型参数下的隐变量的估计,这一步给出了更接近于
- M步(固定
,优化
),
,作为下一轮的迭代参数,即最大化
的下界:
,这一步则是在提高
EM算法被证明是可以收敛的,也即是说该分类算法总能够有效的分类数据。
六 应用与推广
EM算法的典型应用和推广包括:
- 求解高斯混合模型(GMM, Gaussian Mixed Model)问题,(即前文所提到的男女生身高问题);
- 隐式马尔可夫模型 (HMM, Hidden Markov Model)中的参数估计问题,其求解算法Baum-Welch算法就是一种EM算法,参考这篇文章;
- KMeans算法在正是GMM在极限情况(高斯分布的极限情况,狄拉克分布)下的特例,参考《Pattern Recognition and Machine Learning》中Mixture Models and EM章节 。
参考文献
李航《统计学习方法》第9章EM算法及其推广
Expectation Maximization
https://zhiyzuo.github.io/EM/
EM Tutorial
http://ai.stanford.edu/~chuongdo/papers/em_tutorial.pdf
EM算法实现:
https://people.duke.edu/~ccc14/sta-663/EMAlgorithm.html
扩展阅读
Hinton和Jordan理解的EM算法
https://mp.weixin.qq.com/s/scx4Rrzyt_Z4kI24A2quzQ
通俗易懂讲明白 最大似然和EM算法
https://mp.weixin.qq.com/s/4DXMfLjr9zaKjICM7HykSg
极大似然估计与最大后验概率估计
https://www.jianshu.com/p/f9d56aeab75e
请问如何用数学方法证明K-means是EM算法的特例?
https://www.zhihu.com/question/49972233?sort=created
EM算法系列(二)-Jenson不等式
https://www.jianshu.com/p/9115f30360a4
如何理解似然函数
https://www.zhihu.com/question/54082000
《Pattern Recognition and Machine Learning》中Mixture Models and EM章节
吴恩达CS229 Lecture Note:
http://cs229.stanford.edu/notes/cs229-notes8.pdf
EM算法的可视化
https://medium.com/@chloebee/the-em-algorithm-explained-52182dbb19d9
好了,今天ARGO的EM算法就讲到这了。其生有涯,机器学习之海也无涯,祝大家好好学习,天天向上~~