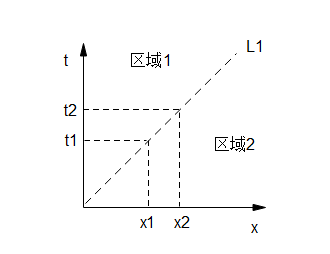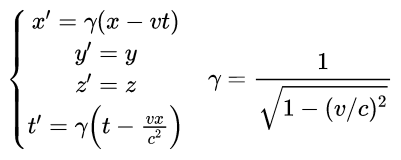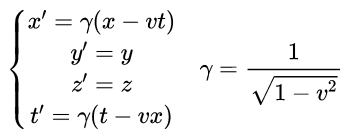07时空图
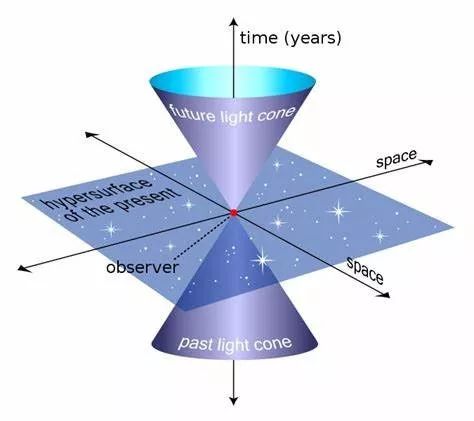
在时空图里,你能非常自然地感觉到时间和空间被统一起来了,因为时空图里的时间轴和空间轴有着完全的平等的地位。
在时空图里,一个粒子现在在哪,你找到它的空间坐标(x,y,z),记下现在的时间t,那么你就得到了它的时空信息(x,y,z,t),那这个时空信息就对应时空图里的一个点,这就叫时空点。
同样的,你再记下它下一个时刻t1的位置(x1,y1,z1),那么它又对应了坐标系的另一个点(x1,y1,z1,t1)。所以,一个粒子在任一时刻的时间、空间信息就都对应了时空图里的一个点。那么,如果考察这个粒子的全部历史,你就可以得到一系列的这种时空点,这些点在时空图里就会形成一条线,这条能代表粒子全部历史的线就叫粒子的世界线。
现实生活里一个粒子有四个维度(三维空间+一维时间),那么对应的坐标轴应该也是四维的,但是我们在二维平面里勉强可以画出三维图形,对四维图形实在无能为力。为了方便起见,我们假设粒子只沿x轴方向运动,这样我们就可以不考虑y轴和z轴的情况,从而把四维的问题简化为二维,然后我们就可以很愉快的在一张二维的纸上画这二维时空图了。
我们先建立一个坐标系,横轴x代表粒子的空间信息,纵轴t代表粒子的时间信息。为了再次简化问题,我们采用几何单位制,也就是取光速c=1,然后我们再来看一些具体问题。
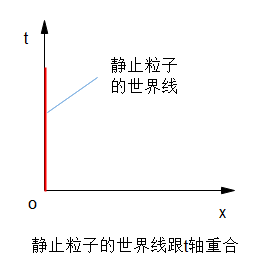
问题1:一个静止不动的粒子在时空图里是什么样的?或者说它的世界线是什么样的?
这个答案很容易想到,一个粒子静止不动,就是在空间上没动,那么它的x坐标一直为零,但是时间依然在流逝,也就是粒子的时间坐标在一直变大。所以,静止不动的粒子是世界线是一条跟t轴重合,垂直于x轴的直线。
问题2:一个匀速向右运动的粒子的世界线是什么样的?
这个也不难想象,一个匀速向右运动的粒子,它在时间轴不停往上走的同时,空间轴上也在不停地往右走,那么这个粒子的世界线应该是一条斜直线。问题是,斜多少?是所有的坐标空间它都可以斜,还是有什么限制?这个问题我们先放着,先看看第三个问题。
问题3:一条朝右上方45°的斜直线(如下图的L1)代表了什么粒子的世界线?
我们先来算一算这个粒子的速度:我们在粒子的世界线L1上取两个点,也就是假设粒子在t1时刻在位置x1,在t2时刻在位置x2。因为这条直线是45°的,所以很显然x2-x1=t2-t1,.那么粒子的速度v=(x2-x1)/(t2-t1)=1。
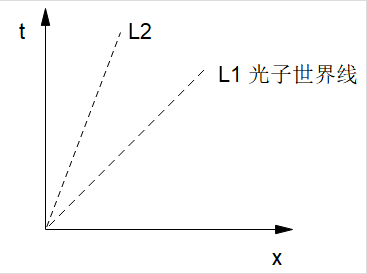
速度等于1是什么意思?我们在画图的时候采用的是几何单位制,也就是取光速c=1(如果我们不采用几何单位制,那么竖轴的单位就不是t,而是ct,本质并没有什么不同)。现在这个粒子的速度等于1,其实就是代表这个粒子的速度是光速,速度是光速那自然就是光子了,那么这条45°斜直线就代表了光子的世界线。
从这里我们可以看到,在时空图里,光子的世界线是45°的斜直线。我们也知道在相对论里任何有质量粒子的速度都是小于光速的,那么一个有质量的粒子做匀速直线运动的世界线该是一条什么样的斜直线呢?是在区域1还是区域2?
我们可以这样想一下:如果粒子的速度比光速小,那么假设粒子在t1时刻在x1处,那么到了t2时刻它肯定到不了x2地方,那么这两点的连线肯定就在L1的上方,也就是区域1。其实我们也可以想一个极端的粒子,假设这个粒子在原点不动,那么粒子的世界线就是跟t轴重合,粒子速度到达光速就是45°的那条直线,那么速度在静止和光速之间的粒子世界线自然就是在区域1的斜直线了。
现在我们知道了这样一个结论:在时空图里,45°的斜直线代表了光子的世界线(如L1),比光子世界线更陡,更加靠近t轴的斜直线(如L2)是有质量粒子匀速直线运动,或者说惯性运动(速度小于光速)的世界线。
有了这样的基本认识,我们来用几何语言分析一下狭义相对论里入门教材里必定会碰到的问题:火车闪光问题。这个问题之所以重要,是因为它揭示了同时的相对性,也就是说在一个惯性系看来是同时发生的事件,在另一个参考系里不一定是同时发生的。爱因斯坦敏锐地发现了这点,然后借此从看似牢不可破的牛顿力学里撕开了一道口子。
08同时的相对性
在牛顿力学里,时间是绝对的,所以同时必然也是一个绝对的词汇。在一个参考系看来是同时发生的事件,不管谁来看都绝对是同时发生的,这也是一个非常符合常识的论述。
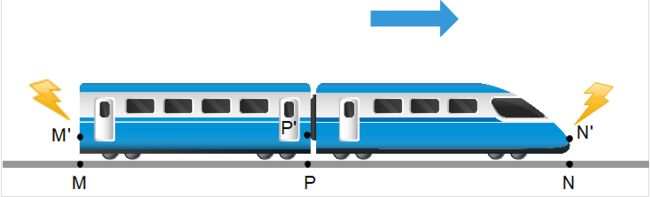
但是,爱因斯坦用一个简单的火车实验就让人们的这个信念坍塌了,这个实验是这样的:假设地面上有一辆匀速运动的火车,在某一个时刻,地面上的观察者发现这个火车的车头和车尾同时被闪电击中。也就是说,对于地面参考系而言,闪电击中车头和车尾这两个事件是同时发生的。但是,爱因斯坦认为在火车参考系里,这两个事件就不是同时发生的。
原因也很简单,我们假设在闪电击中火车头尾的时候,在地面这两点的中点有一个观察者。因为两个事件在地面系看起来是同时发生的,所以,站在地面中间的那个观察者肯定会同时看到车头和车尾发过来的闪光,所以这两个事件是同时的。
但是,站在火车中间的观察者就不是这样了,因为车头车尾的闪光在向中间传播的时候,火车本身也在前进,所以火车中间的人就会先看到车头发过来的闪光,后看到车尾发过来的闪光。所以,火车上的观察者就会觉得这闪电击中车头和车尾这两个事件不是同时发生的,而是击中车头的先,击中车尾的后。
爱因斯坦从这个火车闪光实验出发,发现了同时的相对性,进而打开了狭义相对论的大门。这个实验比较简单,整个逻辑过程也不复杂,但是这样讲不够直观,不够具有普遍性。因为很多人会把这个实验当做一个特例来处理,也就是只有当他们意识到要讲同时的相对性的时候才会想起这个实验,平常就会把这个实验带来的同时的相对性给忘了,然后带来一系列的“相对论诡异疑难”。下面我们从几何语言来看看这个问题,看看如何让这个重要问题更直观,更具有普遍性。
我们假设闪电同时击中车头车尾(从地面系观测)的时候,火车的车尾M’、车头N’刚好经过地面的M和N点,P点为地面MN的中点,P’为火车上的中点,我们来看看怎么在时空图上描述这个闪电击中火车的问题。
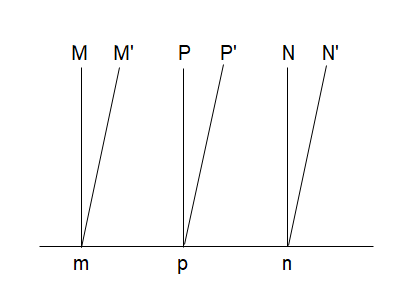
我们先来看看地面上M和N点的世界线,因为M、N在地面上没有动,所以M和N点的世界线都是一条沿着时间轴t竖直向上的直线(空间位置没动,只有时间t在动)。同样的,在MN中间的P点也没动,它的世界线也是一条竖直向上的直线。这三条线好画,那么在火车上的M’、N’和P’,它们都在做匀速直线运动,那它们的世界线是什么样的呢?这个我们上一节刚好说了,做匀速运动的粒子的世界线是一条比45°线更陡的斜直线。那我们把这六个点的世界线都画出来,不难理解应该就是下面这样(横轴为空间x,纵轴为时间t,这里省略了)。
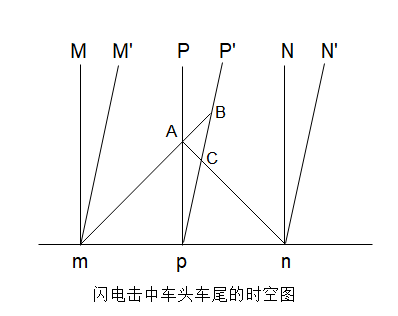
下面是关键的了,怎么画车头、车尾的闪光向中点传播的过程?我们知道,闪电击中车头车尾之后,这个事件就会向四面八方发射光信号(所以四面八方的人都能看到火车被闪电击中了),但是,其他的信号我们都不关心,我们只关心被地面中点P和火车中点P’所接收到的那一束光信号。那么,这个光信号要怎么画呢?它们的出发点肯定在m和n,那接下来呢?这次我们再次想起了上一节中提到的:光子的世界线是45°的斜直线。那么我们就加上这两条45°的世界线,最后的图就是下面这样的。
这两根世界线跟两个中点P、P’的世界线产生了三个交点A、B、C,这是三个很有意思的点,我们来分析一下它们的物理含义。
首先是A点,A点是闪光世界线跟地面中点P点的世界线交点,它们相交了是什么意思?纵轴代表时间,横轴代表空间,相交了就代表这两个粒子此时时间和空间信息都一样,都一样那就是相遇了啊,具体到我们这个问题就是闪光传播到了地面上的中点。因为地面没有动,M和N点到P点的距离又是一样的,那么车头车尾的闪光肯定同时到达地面中点,所以它们都相交于A点是正确的。
再来看B点和C点。B点是车尾的闪光的世界线和火车里面的中点P’世界线的交点,那B点代表的意思自然就是火车中间的观察者观察到车尾的闪光这个事件。同理,C点是车头闪光世界线跟P’世界线的交点,那C点就是火车中间的观察者观察到车头闪光的这个事件。这样看就非常明显了,纵坐标是时间轴,那么B事件明显就是在C事件之后发生的啊。
这正是同时的相对性的表现:对于地面系,它们都交于A点,所以是同时的;对于火车系,它们分别交于B点C点,所以是不同时的,这在时空图里极为直观。
这里有一个事要强调一下:我们在这个火车闪光问题里虽然涉及到了地面系和火车系,但是我们是一直在地面系来分析问题的。我们画的时空图,不管是地面上的点还是火车上的点,我们都是在地面系画,因为毕竟一张图只有一个坐标系嘛。那么,我们能不能在一张图里同时把地面系和火车系两个惯性系都画上呢?
答案当然是可以的。
09两个坐标系
我们来具体看看这个问题:假设我们现在已经画了一个地面系的直角坐标系x-t,那么我们要如何把火车系的坐标系x’-t’画出来?
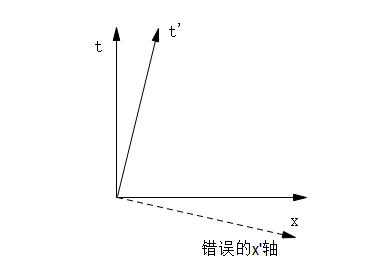
第一次遇到这个问题的同学可能有点懵,不着急我们一步步来,我们先看看火车系的纵轴t’要怎么画。要画火车系的纵轴,我们先想想一个坐标系的纵轴的是什么意思?我们知道如果我们让一个点的横坐标为零,那么这个点的轨迹就是跟纵轴重合的。还记得我们上面说的静止粒子的世界线么?静止粒子的空间坐标x为0,所以它的世界线就是垂直于x轴,与t轴重合的一条直线。那么,火车系的t’轴自然也是在火车系里静止在原点处粒子的世界线。
这一点很重要,大家好好理解一下,也就是说我们只要把火车系处于原点处粒子的世界线画出来,我们就能得到火车系的t’轴。那么,一个在火车系静止的点,在地面系看来它是在做匀速直线运动,而匀速直线运动的点的世界线,我们上面也说了,就是一条比45°更陡的斜直线。所以,火车系的t’轴就是这样一条更陡的斜直线,如下图所示:
火车系的t’轴画好了,那火车系的x’轴呢?大家可以看到我在图上用虚线画了一根与t’垂直的轴,并且特意标明了“错误的x’轴”。为什么要这样标呢?因为这是相对论初学者极容易犯的错误。我们已经习惯了欧式几何,欧式几何里直角坐标系都是相互垂直的,所以到了这里很多人看到我们已经画出了t’轴,就立马条件反射地画一根和t’轴垂直的当做x’轴,但是这是错误的,为什么呢?
这里我们第一次感受到了闵氏几何的异样。我在最开始花了那么大的篇幅告诉大家为什么狭义相对论要使用闵氏几何,我们也知道了闵氏几何的线元跟欧式几何不一样(时间项前面多了一个负号),所以,我们在画时空图处理狭义相对论问题的时候,一定要意识到自己虽然是在欧式平面里画图,但是我们画的是闵氏几何里的图形。
有人可能会有点疑问,我们前面不是已经用时空图解决了同时的相对性问题么?我们不是已经把爱因斯坦火车闪光问题用时空图画出来了么,我没感觉啥异样啊?那只是因为那个问题比较简单:它只有一个坐标系,而且也不涉及到线长相关的问题,所以我即便在一个欧式直角坐标系里把它画出来了,它也暂时没什么冲突。如果我们生活在一个闵氏空间里,那么我们画出的闵氏直角坐标系肯定都是相互垂直的,但是我们生活在欧式空间里,我已经用一个欧式空间里的直角坐标系画了一个闵氏坐标系,那么另一个就肯定不可能再是垂直的了。
这里的逻辑有点绕,大家可以细细品味,搞得不是很懂也不要紧,我接下来会把另一个坐标系画出来,大家能看懂再回去看上面的一段话就明白了。
好,回到正题,我们再来看看火车系正确的x’轴该怎么画。我们再来整体回顾一下这个事情:我们现在是已经画好了地面系x-t,要画火车系x’-t’,火车系和地面系它有没有什么关系呢?有啊,洛伦兹变换说的不就是地面系和火车系的关系么?什么是洛伦兹变换?比如我在地面系观测到了一个粒子的位置和速度,现在我想知道它在火车系里是什么情况,我并不需要重新再到火车系里测量一遍这个粒子的位置和速度,我只需要根据洛伦兹变换就可以直接得到火车系里那个粒子的运动情况。所以,洛伦兹变换就是两个惯性系之间的联系,我只要知道了一个惯性系里粒子的运动情况,立马我就可以知道其他惯性系里粒子运动的情况。
所以,我们可以根据洛伦兹变换来找到两个惯性系之间的联系。我现在不是根据地面系的坐标轴来找火车系的坐标轴么?我们对着洛伦兹变换改就是了。洛伦兹变换是下面这样的:
其中,x,y,z,t代表地面系里观测到的,x’,y’,z’,t’是火车系里观测到的。v是火车系相对地面系的速度,火车的速度一旦给定了,这个v就是一个定值,c是光速,所以右边的γ都是一个常数。如果我们再根据几何单位制来,取c=1,那么洛伦兹变换就可以简化成下面的样子:
因为我们只考虑火车系相对地面系在x轴方向上的运动,所以在y和z方向上还跟原来一样,我们可以不考虑。我们现在画图也是来画x-t图,所以我们重点关注这两个式子:
这是什么呢?这不就是火车系了的x’和t’么?我现在要画的就是x’的坐标轴,也就是火车系的空间坐标轴,那怎么找到这个坐标轴呢?这个我们前面也提过:纵坐标的那条线就是横坐标为0的所有点的集合,反过来也是,横坐标就是纵坐标为0的点的集合。所以,我们令火车系的时间等于0,也就是纵坐标t’=0就能找到横坐标x’轴了。
那我们令t’=γ(t-vx)=0,因为γ是一个不为零的常数,所以就只有t-vx=0了,也就是t=vx。
这在x-t坐标系里就是一条过原点的直线,斜率为火车的速度v(斜率就是这条直线的倾斜程度,你可以理解为一个坡越陡斜率越大。当直线与横轴重合的时候,斜率为0;当直线跟横轴成45°的时候,斜率为1;当直线跟纵轴重合的时候,斜率为无穷大)。因为我们这里是几何单位制,光速为1,在狭义相对论里任何有质量的物体它的运动速度都是小于光速的,所以火车的速度v肯定是小于1的,也就是说这条直线的斜率比45°的直线(刚好是光的世界线)小。
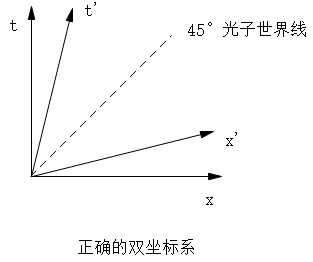
再者,我们可以用同样的方法令x’=γ(x-vt)=0,就能得到火车系的纵轴是这样一条直线:t=x/v。它的斜率是1/v,因为v小于1,所以1/v是个大于1的数,所以这条斜直线的斜率比45°要大(我们前面画的也正是这样)。这里我给一个初中数学的结论:斜率互为倒数(比如v和1/v)的两条直线它们是关于y=x,也就是45°的直线对称的。所以,我们的x’轴是跟t’轴关于45°的直线对称的。这样我们就能精确地把它画出来了,如下图:
第一次看到这样一个坐标系的同学可能会感觉非常别扭,为什么火车系x’-t’的坐标系不是正交的,不是一个直角呢?我们得这样看:它们是正交的,只不过它们是在闵氏几何里正交,我们现在强行把它画在欧式几何里,那么肯定就看起来不正交了。
还有同学也会有疑惑,你不是说狭义相对论里惯性系都是平权的么?那么为什么这里把地面系画成直角的,而把火车系画成了一个小于直角的坐标系?我要是人就在火车里,我非要把火车系画成直角的,不行么?行,当然行。你可以按照上面的思路把火车系画成直角的基准系,再反推过去画地面系,最终的两个图虽然形状不一样,但是实质上还是等价的。
理解这个双坐标系非常关键,它第一次向我们展示了闵氏几何不一样的地方。有了它,我们就可以很方便的处理不同惯性系里的一些事情,比如,我们喜闻乐见的尺缩效应。
公众号:长尾科技